Enotski krog je krog s polmerom 1. Središče enotskega kroga je v izhodišču (0,0) na osi. The obseg enotskega kroga je 2π enot, medtem ko je površina enotskega kroga π enot2. Nosi vse lastnosti kroga. Enotski krog ima enačbo x2+ in2= 1. Ta enotski krog pomaga pri definiranju različnih trigonometričnih konceptov.
Krog enote
Krog enote je pogosto označen kot S1posplošitev na višje dimenzije je sfera enote. V nadaljevanju si podrobneje oglejmo več o enotskem krogu, formuli in rešenih primerih.
Kaj je enotni krog?
Enotski krog je krog s polmerom ene (1) enote. Za risanje enotskega kroga uporabljamo kartezično ravnino, enotski krog pa je 2-stopenjski polinom z dvema spremenljivkama. Enotski krog ima različne aplikacije v trigonometriji in algebri in se večinoma uporablja za iskanje vrednosti različnih trigonometričnih razmerij, kot so sin x, cos x, tan x in druga.
Definicija kroga enote
V matematiki enotski krog definiramo kot geometrijsko mesto fiksne točke, ki je od središča kroga oddaljena eno enoto. Enotski krog ima polmer ene enote in od tod tudi ime enotski krog.
Enačba enotskega kroga
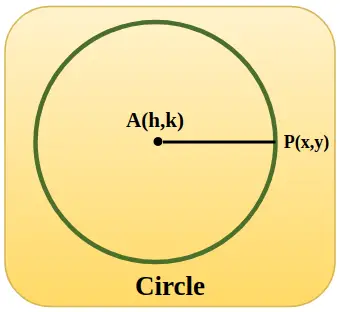
Vemo, da je enačba katerega koli kroga s središčem (h, k) in polmerom 'r':
(x – h) 2 + (y – k) 2 = r 2
Za enotski krog vemo, da je r 1 enota, zato je enačba enotskega kroga
(x – h) 2 + (y – k) 2 = 1
Formula enotskega kroga
Če je središče enotskega kroga izhodišče, tj. (h, k) = (0, 0), potem je enačba enotskega kroga
x 2 + in 2 = 1
Na spodnji sliki je predstavljen enotski krog s središčno koordinato h, k in ko je krog v izhodišču, je vrednost h in k enaka nič, polmer AP pa je enak 1 enoti.
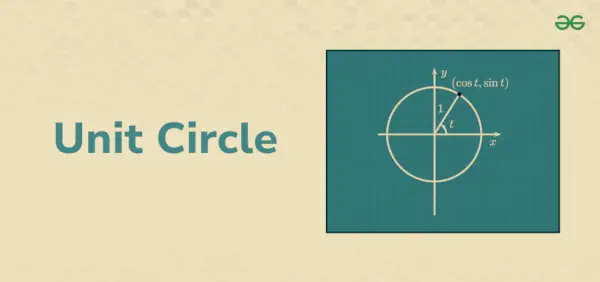
Trigonometrične funkcije z uporabo enotskega kroga
Uporabo Pitagorovega izreka v enotskem krogu je mogoče bolje uporabiti za razumevanje trigonometričnih funkcij. Za to menimo, da je pravokotni trikotnik postavljen znotraj enotskega kroga v kartezični koordinatni ravnini. Če opazimo, polmer tega kroga označuje hipotenuzo pravokotnega trikotnika.
Polmer kroga tvori vektor. To vodi do oblikovanja kota, recimo θ s pozitivno osjo x. Recimo, da je x osnovna dolžina in y višinska dolžina pravokotnega trikotnika. Prav tako sta koordinati končnih točk radijskega vektorja (x, y).
Pravokotni trikotnik ima stranice 1, x oziroma y. Trigonometrično razmerje lahko zdaj izračunamo na naslednji način:
sin θ = nadmorska višina/hipotenuza = y/1
cos θ = osnova/hipotenuza = x/1
zdaj,
- sin θ = y
- cos θ = x
- tan θ = sin θ /cos θ = y/x
Če zamenjamo vrednosti θ, lahko dobimo glavne vrednosti vseh trigonometričnih funkcij. Podobno se najdejo vrednosti trigonometričnih funkcij pri različnih vrednostih.
Krog enote s Sin Cos in Tan
Vsaka točka na enotskem krogu s koordinatami (x, y) je predstavljena s trigonometričnimi identitetami kot (cosθ, sinθ). Koordinate vogalov polmera predstavljajo kosinus in sinus vrednosti θ za določeno vrednost θ in črto radija. Imamo cos θ = x in sin θ = y. Obstajajo štirje deli kroga, ki ležijo v enem kvadrantu in tvorijo kot 90°, 180°, 270° in 360°. Vrednosti polmera so med -1 in 1. Poleg tega sta vrednosti sin θ in cos θ med 1 oziroma -1.
Enotski krog in trigonometrične identitete
Trigonometrične identitete enotskega kroga za kotangens, sekans in kosekans je mogoče izračunati z uporabo identitet za sin, cos in tan. Končno dobimo pravokotni trikotnik s stranicami 1, x oziroma y. Računanje identitete enotskega kroga je mogoče izraziti kot,
- sin θ = y/1
- cos θ = x/1
- tan θ = y/x
- s θ = 1/x
- cosec θ = 1/y
- posteljica θ = x/y
Krožni diagram enot
Diagram enotskega kroga je grafikon, ki vsebuje vrednost trigonometrične funkcije sinusa in kosinusa za različne kote. Grafikon enotskega kroga za isto je dodan spodaj,
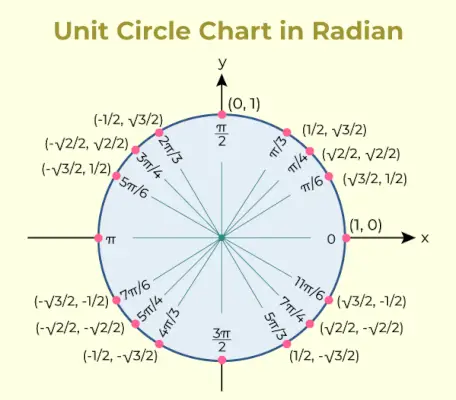
Krožna tabela enot
Trigonometrična razmerja, uporabljena v tabeli enotskega kroga, se uporabljajo za navajanje koordinat točk na enotskem krogu, ki ustrezajo skupnim kotom.
| Koti | 0° | 30° | 45° | 60° | 90° |
|---|---|---|---|---|---|
| brez | 0 | 1/2 | 1/√(2) | √3/2 | 1 |
| cos | 1 | √3/2 | 1/√(2) | 1/2 | 0 |
| torej | 0 | 1/√(3) | 1 | √ (3) | Ni definirano |
| csc | Ni definirano | 2 | √ (2) | 23) | 1 |
| sek | 1 | 23) | √ (2) | 2 stavek bash if | Ni definirano |
| otroška posteljica | Ni definirano | √ (3) | 1 | 1/√(3) | 0 |
Pitagorejske identitete enotnega kroga
Obstajajo tri pitagorejske identitete in vse jih je enostavno dokazati z uporabo koncepta enotskega kroga, tri pitagorejske identitete so,
- brez2θ + cos2θ = 1
- 1 + torej2θ = sekunda2jaz
- 1 + otroška posteljica2θ = cosec2jaz
Enotski krog Kompleksna ravnina
Kompleksna števila in kompleksno ravnino je enostavno razložiti s konceptom enotskega kroga. Enačba enotskega kroga v kompleksni obliki je,
|z| = 1
ALI
x 2 + in 2 = 1
V Eulerjevi obliki je kompleksno število predstavljeno kot
z = e to = cos t + i(sin t)
Preberi več
Rešeni primeri na enotskem krogu
V1: Dokažite, da točka Q leži na enotskem krogu, Q = [1/√(6), √4/√6]
rešitev:
podano,
- Q = [1/√(6), √4/√6]
x = 1/√(6), y = √4/√6
Enačba enotskega kroga je,
x2+ in2= 1
LHS = (1/√(6))2+ (√4/√6)2
LHS = 1/6 + 4/6 = 5/6 ≠ 1
LHS ≠ RHS
Tako točka Q[1/√(6), √4/√6] ne leži na enotskem krogu.
V2: Izračunajte torej 30 O z uporabo vrednosti sin in cos enotskega kroga.
rešitev:
tan 30° z uporabo vrednosti sin in cos,
tan 30° = (sin 30°)/ (cos 30°)
- brez 30° = 1/2
- cos 30° = √(3)/2
tan 30° = 1/2/√(3)/2
tan 30° = 1/√(3)
V3: Preverite, ali točka P [1/2, √(3)/2] leži na enotskem krogu.
rešitev:
podano,
P = [1/2, √(3)/2]
- x = 1/2
- y = √(3)/2
Enačba enotskega kroga je,
- x2+ in2= 1
LHS
= (1/2)2+ (√(3)/2)2
= 1/4 + 3/4
= (1 + 3)/4 = 4/4
= 1
= RHS
Vprašanja za vadbo o krogu enot
Q1. Preverite, ali ležita točki A (1/2, 3/2) na enotskem krogu.
Q2. Preverite, ali ležita točki A (2, 1/2) na enotskem krogu.
Q3. Poiščite vrednost cos 240°
Q4. Poiščite vrednost tan 320°
V5. Poiščite vrednost sin 160°
Krog enote – pogosta vprašanja
Kaj je enotni krog?
Enotski krog je definiran kot lokacija točke, ki je eno enoto oddaljena od fiksne točke. Ima središče v (0,0) in vrednost njegovega polmera je 1.
Kako preveriti, ali točka leži na krogu enote?
Vsaka točka, ki leži v 2D ravnini in ima obliko (x, y), se postavi v enačbo enotskega kroga x2+ in2= 1, da preverimo, ali leži na krogu ali ne.
Kakšna je formula enotskega kroga?
Formula enotskega kroga je formula, ki se uporablja za algebraično predstavitev enotskega kroga. Formula enotskega kroga je podana kot
x 2 + in 2 = 1
Zakaj se imenuje krog enot?
Enotski krog se imenuje enotski krog, ker ima polmer ene (1) enot.
