Trigonometrična tabela je standardna tabela, ki nam pomaga najti vrednosti trigonometričnih razmerij za standardne kote, kot so 0°, 30°, 45°, 60° in 90°. To sestavlja vseh šest trigonometričnih razmerij: sinus, kosinus, tangens, kosekans, sekans in kotangens.
Spoznajmo podrobneje trigonometrično tabelo.
Kazalo
- Trigonometrična tabela
- Tabela trigonometričnih funkcij
- Trik za učenje trigonometričnih razmerij
- Kako si zapomniti trigonometrično tabelo
- Kako ustvariti trigonsko tabelo
- Trigonometrične formule
- Tabela trigonometričnih identitet
- Primeri trigonometričnih tabel
Trigonometrična tabela
Trigonometrična tabela je razporeditev vrednosti vseh šestih trigonometričnih funkcij za njihove skupne kote v obliki tabele.
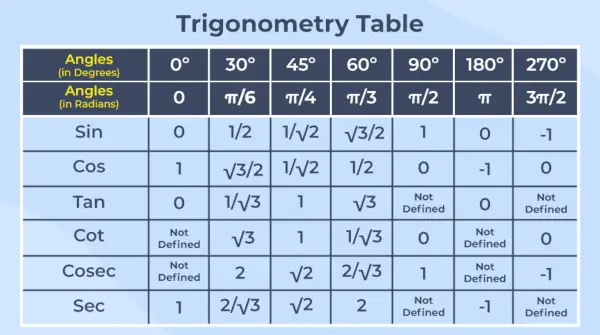
Opomba – Trigonometrija je veja matematike, ki se ukvarja z razmerji med koti in stranicami pravokotnih trikotnikov.
Tabela trigonometričnih funkcij
Trigonometrija ima 6 osnovnih trigonometričnih funkcij: sinus, kosinus, tangens, kosekans, sekans in kotangens. Zdaj pa poglejmo trigonometrične funkcije.
Za vsak pravokotni trikotnik s pravokotnico (P), osnovo (B) in hipotenuzo (H) je šest trigonometričnih funkcij naslednjih:
| Tabela trigonometričnih funkcij | |||
| funkcija | Opredelitev | Zastopanje | Razmerje s stranicami pravokotnega trikotnika |
| Njegovo | Razmerje med pravokotnico in hipotenuzo | brez jaz | Nasprotna stran / hipotenuza |
| Kosinus | Razmerje med osnovo in hipotenuzo | cos jaz | Sosednja stran / hipotenuza |
| Tangenta | Razmerje med sinusom in kosinusom kota | torej jaz | Nasprotna stran / sosednja stran |
| Kosekans | Recipročna vrednost greha θ | csc jaz ali cosec jaz | Hipotenuza / Nasprotna stran |
| Sekant | Recipročna vrednost cos θ | sek jaz | Hipotenuza / sosednja stran |
| Kotangens | Recipročna vrednost tan θ | posteljica jaz | Sosednja stran / Nasprotna stran |
Opomba – Trigonometrija je veja matematike, ki se ukvarja z razmerji med koti in stranicami trikotnikov, zlasti pravokotnih trikotnikov. Vključuje preučevanje in uporabo sinusa, kosinusa, tangensa in drugih trigonometričnih funkcij za reševanje problemov na različnih področjih.
Preverite : Trigonometrija: formule, tabela, identitete in razmerja
Trik za učenje trigonometričnih razmerij
Preučite spodnjo tabelo, da se naučite trigonometričnih razmerij na način, ki si ga je lahko zapomniti.
| Nekateri ljudje imajo skodrane črne lase, da ustvarjajo lepoto |
| sin θ (nekaj) = pravokotnik (ljudje) / hipotenuza (imajo) |
| cos θ (kodrast) = osnova (črna) / hipotenuza (las) |
| tan θ (do) = pravokotno (proizvaja) / osnova (lepota) |
Kako si zapomniti trigonometrično tabelo
Trigonometrično tabelo si je zelo enostavno zapomniti, če poznate vse trigonometrične formule. Obstaja tudi trik, imenovan trik z eno roko zapomni si trigonometrično tabelo.

Korak 1: Na zgornji sliki za sinusno tabelo preštejte prste na levi strani za standardni kot.
2. korak: Število prstov na levi strani (izračunajte v 1. koraku) delite s 4
3. korak: Poiščite kvadratni koren vrednosti, izračunane v 2. koraku.
Preverite: Trigonometrične formule – seznam vseh trigonometričnih identitet in formul
Kako ustvariti trigonsko tabelo
Preučite naslednje korake, da ustvarite trigonometrično tabelo za standardne kote.
1. korak: Ustvarite tabelo
Ustvarite tabelo in navedite vse kote, kot npr 0°, 30°, 45°, 60° in 90°, v zgornji vrsti. V prvi stolpec vnesite vse trigonometrične funkcije sin, cos, tan, cosec, sec in cot.
2. korak: Ocenite vrednost za vse kote funkcije sin.
Za iskanje vrednosti funkcije sin delite 0, 1, 2, 3 in 4 s 4 in vzemite pod koren vsake vrednosti kot,
Kajti vrednost sin 0° = √(0/4) = 0
Podobno,
sin 30° = √(1/4) = 1/2
sin 45° = √(2/4) = 1/√2
sin 60° = √(3/4) = √3/2
sin 90° = √(4/4) = 1
| brez 0° | brez 30° | brez 45° | brez 60° | brez 90° |
|---|---|---|---|---|
| 0 | 1/2 | 1/√2 | √3/2 | 1 |
3. korak: Ocenite vrednost za vse kote funkcije cos
Vrednost funkcije cos je nasprotna vrednosti funkcije sin, tj. cos 0° = sin 90°, cos 30° = sin 60° in cos 45° = sin 45°, torej
| cos 0° | cos 30° | cos 45° | cos 60° | cos 90° |
|---|---|---|---|---|
| 1 | √3/2 | 1/√2 | 1/2 | 0 |
4. korak: Ocenite vrednost za vse kote funkcije tan
Vrednost funkcije tan je enaka funkciji sin, deljeni s funkcijo cos, tj. tan x = sin x / cos x. Vrednost vseh kotov v funkciji tan se izračuna kot,
niz v celo število
tan 0°= sin 0° / cos 0° = 0/1 = 0, podobno
| torej 0° | torej 30° | torej 45° | torej 60° | torej 90° |
|---|---|---|---|---|
| 0 | 1/√3 | 1 | √3 | Ni definirano |
5. korak: Ocenite vrednost za vse kote funkcije cosec
Vrednost funkcije cosec je enaka recipročni vrednosti funkcije sin. Vrednost cosec 0° dobimo tako, da vzamemo recipročno vrednost sin 0°
cosec 0° = 1 / sin 0° = 1 / 0 = Ni določeno. Podobno,
| cosec 0° | cosec 30° | cosec 45° | cosec 60° | cosec 90° |
|---|---|---|---|---|
| Ni definirano | 2 | √2 | 23 | 1 |
6. korak: Ocenite vrednost za vse kote funkcije sec
Vrednost funkcije sec je enaka recipročni vrednosti funkcije cos. Vrednost sec 0° dobimo tako, da vzamemo recipročno vrednost cos 0°
sec 0° = 1 / cos 0° = 1 / 1 = 1. Podobno je
| sek 0° | sek 30° | sek 45° | sek 60° | sek 90° |
|---|---|---|---|---|
| 1 | 23 | √2 | 2 | Ni definirano |
7. korak: Ocenite vrednost za vse kote funkcije posteljice
Vrednost funkcije cot je enaka recipročni vrednosti funkcije tan. Vrednost cot 0° dobimo tako, da vzamemo recipročno vrednost tan 0°
posteljica 0° = 1 /tan 0° = 1 / 0 = Ni določeno. Podobno,
| posteljica 0° | posteljica 30° | posteljica 45° | posteljica 60° | posteljica 90° |
|---|---|---|---|---|
| Ni definirano | √3 | 1 | 1/√3 | 0 |
Na ta način lahko ustvarimo naslednjo tabelo trigonometričnih razmerij:
| Trigonometrična tabela stopinj in radianov | |||||||
|---|---|---|---|---|---|---|---|
| Kot (v stopinjah) | Kot (v radianih) | brez | Cos | torej | Cosec | Sec | Otroška posteljica |
| 0° | 0 | 0 | 1 | 0 | Nedoločeno | 1 | Nedoločeno |
| 30° | str/6 | 1/2 | √3/2 | 1/√3 | 2 | 23 | √3 |
| 45° | str/4 | √2/2 | √2/2 | 1 | √2 | √2 | 1 |
| 60° | p/3 | √3/2 | 1/2 | √3 | 23 | 2 | 1/√3 |
| 90° | p/2 | 1 | 0 | Nedoločeno | 1 | Nedoločeno | 0 |
Trigonometrične formule
Spoznajmo nekaj trigonometričnih formul, povezanih s komplementarnimi in dodatnimi koti.
- Komplementarni koti: Par kotov, katerih vsota je enaka 90°
- Dodatni koti: Par kotov, katerih vsota je enaka 180°
Preverite: Trigonometrična razmerja
Trigonske identitete komplementarnih kotov
Identitete komplementarnih kotov temeljijo na razmerju med trigonometričnima funkcijama dveh kotov, ki seštejejo do 90 stopinj (ali π/2 radiana). Ti so znani kot sodelujoče identitete .
| Trigonometrična funkcija | Identiteta |
|---|---|
| Njegovo | sin(90°− jaz )=cos jaz |
| Kosinus | cos(90°− jaz )=brez jaz |
| Tangenta | tan (90°− jaz )=otroška posteljica jaz |
| Kotangens | posteljica (90°− jaz )=tako jaz |
| Sekant | sec(90°− jaz )=csc jaz |
| Kosekans | cosec(90°− jaz )=sek jaz |
Trigonske identitete dopolnilnih kotov
Identitete dodatnih kotov se nanašajo na trigonometrične funkcije dveh kotov, ki skupaj znašajo 180 stopinj (ali π radianov).
| Trigonometrična funkcija | Identiteta |
|---|---|
| Njegovo | sin(180°− jaz )=brez jaz |
| Kosinus | cos(180°− jaz )=−cos jaz |
| Tangenta | tan (180°− jaz )=−tan jaz |
| Kotangens | posteljica (180°− jaz )=−otroška posteljica jaz |
| Sekant | sec(180°− jaz )=−sek jaz |
| Kosekans | cosec(180°− jaz )=cosec jaz |
Tabela trigonometričnih identitet
Trigonometrične identitete so identitete, ki se pogosto uporabljajo pri reševanju trigonometričnih problemov. Obstajajo različne trigonometrične identitete, vendar so tri glavne trigonometrične identitete:
| Tabela trigonometričnih identitet | |
| Trigonometrična identiteta | Formula |
| Pitagorejska identiteta | brez2θ + cos2θ = 1 |
| Sekantno-tangentna istovetnost | sek2θ – torej2θ = 1 |
| Kosekans-kotangentna istovetnost | cosec2θ – posteljica2θ = 1 |
Preverite tudi:
- Trigonometrična razmerja
- Inverzne trigonometrične identitete
- Višine in razdalje
Primeri trigonometričnih tabel
Rešimo nekaj vprašanj na trigonometrični tabeli.
Primer 1: Če je sin θ = 4/5, poiščite vse trigonometrične vrednosti.
rešitev:
Tukaj imamo,
sin θ = 4/5
kot, sin θ = pravokotnik / hipotenuza
tako imamo pravokotnico (P) = 4 in hipotenuzo (H) = 5
Torej po Pitagorovem izreku H 2 = P 2 +B 2
Ugotovimo vrednost osnove (B)
52= B2+ 42
25 = B2+ 16
25 -16 = B2
B2= 9
B = 3Zdaj imamo,
Sin θ = pravokotnik/hipotenuza
= AB/AC = 4/5Kosinus θ = osnova/hipotenuza
= BC/AC = 3/5Tangenta θ = pravokotnik/osnova
= AB/BC = 4/3Kosekans θ = hipotenuza/pravokotnik
= AC/AB = 5/4Sekans θ = hipotenuza/osnova
= AC/BC = 5/3Kotangens θ = osnova/navpičnica
= BC/AB = 3/4
Primer 2: Poiščite vrednost cos 45° + 2 sin 60° – tan 60°.
rešitev:
Iz trigonometrične tabele,
cos 45° = 1/√2, sin 60° = √3/2 in tan 60° = √3
torej
cos 45° + 2 sin 60° – tan 60° = 1/√2 + 2(√3/2) – √3
= 1/√2
Primer 3: Poiščite vrednost cos 75°.
rešitev:
Vemo, da
cos 75° = cos (45° + 30°) {as, cos (A + B) = cos A cos B – sin A sin B}
= cos 45° cos 30° – sin 45° sin 30°
= 1/√2 × √3/2 – 1/√2 × 1/2
= (√3 – 1)/2√2cos 75°= (√3 – 1)/2√2.
Zaključek – Trigonometrična tabela
Trigonometrična tabela ponuja izčrpno referenco za trigonometrične funkcije sinus, kosinus, tangens, kosekans, sekans in kotangens, skupaj z njihovimi vrednostmi za različne kote. jaz t služi kot dragoceno orodje za reševanje trigonometrične enačbe, analiziranje geometrijskih odnosov in razumevanje obnašanja periodičnih pojavov. Ali v matematike, fizike, inženiringa ali drugih področij, trigonometrična tabela pomaga pri izračunih, reševanju problemov in vizualizaciji ter prispeva k globljemu razumevanju trigonometričnih konceptov in njihovih aplikacij v scenarijih resničnega sveta.
Trigonometrična tabela – pogosta vprašanja
Kaj je trigonometrija?
Trigonometrija je veja matematike, ki se ukvarja s kotom in stranicami katerega koli trikotnika.
Kaj je trigonometrična tabela?
Trigonometrična tabela je tabela, ki vsebuje vrednosti vseh šestih trigonometričnih funkcij za skupne kote.
Kdo je izumil trigonometrično tabelo?
Grški astronom Hiparh (127 pr. n. št.) izumil trigonometrično tabelo.
Kaj so standardni koti v trigonometrični tabeli?
Standardni koti v trigonometrični tabeli so 0°, 30°, 45°, 60° in 90°
Kakšna je vrednost porjavelosti 45 stopinj?
Vrednost tan 45 stopinj je 1.
Kako se naučiti trigonometrične tabele?
Trik za učenje trigonometrične tabele je,
- Naučiti se morate vseh vrednosti vseh kotov sin funkcije.
- Vrednost vseh kotov funkcije cos je zrcalna slika funkcije sin.
- Vrednosti funkcije tan lahko izračunate tako, da funkcijo sin delite s funkcijo cos.
- Vrednost funkcije cosec je recipročna sin.
- Podobno sta sec in cot recipročni funkciji cos in cot.
Kaj je šest osnovnih funkcij v trigonometrični tabeli?
Šest osnovnih trigonometričnih funkcij v trigonometrični tabeli je sinus, kosinus, tangens, sekans, kotangens in kosekans.
Ali obstajajo kalkulatorji, ki lahko nadomestijo trigonometrične tabele?
Znanstveni kalkulatorji lahko izračunajo trigonometrična razmerja za kateri koli kot8.
Kakšna je uporaba trigonometrične tabele?
Trigonometrična tabela se v bistvu uporablja za iskanje vrednosti vseh trigonometričnih razmerij za vse kote. Te vrednosti imajo številne aplikacije v resničnem življenju.
