Kompleksna števila so naravno nadaljevanje realnih števil. V moderni dobi se kompleksna števila uporabljajo na številnih področjih, kot so digitalna obdelava signalov, kriptografija in številna področja, povezana z računalnikom.

V tem članku bomo spoznali imaginarna števila, kompleksna števila in njihove vrste, različne operacije s kompleksnimi števili, lastnosti kompleksnih števil, uporabo kompleksnih števil itd.

Definicija kompleksnih števil

Kompleksna števila so številke obrazca (a + i b) kje a & b so prave številke in jaz je namišljena enota, imenovana jota, ki predstavlja √-1. Na primer, 2 + 3i je kompleksno število, v katerem je 2 realno število, 3i pa imaginarno število. Kompleksna števila lahko zapišemo kot a + ib, kjer sta a in b racionalni števili, ki ju lahko predstavimo na številski premici, ki se razteza na neskončnost .

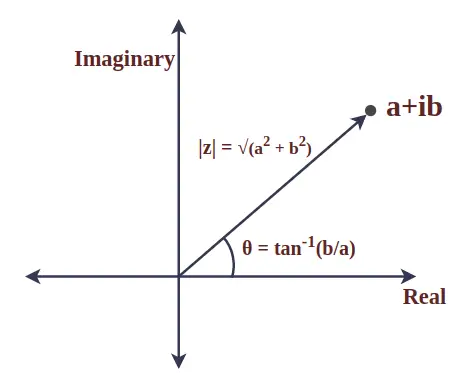
Modul kompleksnega števila

Modul kompleksnega števila je absolutna vrednost in predstavlja razdaljo med izhodiščem in dano točko. Znana je tudi kot velikost kompleksnega števila. Vzemimo kompleksno število z = a + ib, potem je modul z definiran kot:

|z| = √(a ² + b ² )

kje,

• a je realni del kompleksnega števila z in
• b je imaginarni del kompleksnega števila z.

Argument kompleksnega števila

Kot med vektorjem radija kompleksnega števila in pozitivno osjo x se imenuje argument kompleksnega števila. Za kompleksno število z = a + ib je matematično podano z:

θ = tan ^-1 (b/a)

kje,

• a je realni del kompleksnega števila z in
• b je imaginarni del kompleksnega števila z.

Moč i(jote)

I(jota) je opredeljena kot kvadratni koren iz -1. Tako lahko vsako potenco i izrazimo kot ponavljajoče se množenje i samega, tj.

• i = √(-1)
• jaz²= -1
• jaz³= – i
• jaz⁴= 1
• jaz⁵= i
• jaz⁶= – 1
• in tako naprej..

Potreba po kompleksnih številih

V starih časih so ljudje poznali samo naravna števila kot ta številke so po naravi najbolj intuitivne, saj jih človeški možgani že razumejo z uporabo vizualnih podob stvari, kot so ovce in hrana. Tako imamo samo množico naravnih števil ( N ), vendar v naravnih številih ni rešitve enačbe x + a = b (a> b) in a, b ∈ N. Tako je nastala razširitev naravnih števil, tj. Cela števila ( jaz ).

Zdaj spet v tem nizu števil ni rešitve enačbe, ax = b (a ≠ 0) in a, b ∈ I, kjer sta a in b oba cela števila. Tako se množica celih števil (I) razširi na množico racionalnih števil ( Q ).

Tudi v tej množici racionalnih števil ni rešitve enačbe x²= a (a> 0) in a ∈ Q. Torej, Q se razširi tako, da vključuje številke, tako da je x²= a(za a> 0) tj. iracionalna števila. Ta niz se imenuje Realna števila in je predstavljen z R .

Dolgo časa je veljalo, da nam ni treba razširiti tega nabora realnih števil, da bi oblikovali še en večji nabor, saj se ta zbirka števil zdi popolna. Toda spet se je pojavila nova težava v tej množici števil, to je, da ni realnega števila, takega, da je x²= a (a <0) in a ∈ R. Tako je množica realnih števil nadalje razširjena, da vključuje vsa takšna vrednotena in poimenovana ta množica kompleksna števila in je predstavljena z C .

Klasifikacija kompleksnih števil

Kot vemo, je standardna oblika kompleksnega števila z = (a + i b) kjer je a, b ∈ R in i je jota (namišljena enota). Glede na vrednosti a (imenovan realni del) in b (imenovan imaginarni del) so kompleksna števila razvrščena v štiri vrste:

• Ničelno kompleksno število
• Čisto realna števila
• Čisto imaginarne številke
• Imaginarne številke

Spoznajmo te vrste podrobneje.

Ničelno kompleksno število

Za katero koli kompleksno število z = a + ib, če je a = 0 & b = 0, se kompleksno število imenuje ničelno kompleksno število. Na primer, edini primer tega je 0.

Čisto realna števila

Za katero koli kompleksno število z = a + ib, če je a ≠ 0 & b = 0, se kompleksno število imenuje čisto realno število, tj. število brez imaginarnega dela. Vsa realna števila so primeri tega, kot so 2, 3, 5, 7 itd.

Čisto imaginarne številke

Za katero koli kompleksno število z = a + ib, če je a = 0 & b ≠ 0, se kompleksno število imenuje čisto imaginarno število, tj. število brez realnega dela. Vsa števila brez realnih delov so primeri te vrste števil, npr. -7i, -5i, -i, i, 5i, 7i itd.

Imaginarne številke

Za katero koli kompleksno število z = a + ib, če je a ≠ 0 & b ≠ 0, se kompleksno število imenuje namišljeno število . Na primer (-1 – i), (1 + i), (1 – i), (2 + 3i) itd.

Različne oblike kompleksnih števil

Obstajajo različne oblike kompleksnih števil,

• Pravokotna oblika
• Polarna oblika
• Eksponentna oblika

Zdaj pa se o njih podrobneje seznanimo.

Pravokotna oblika

Pravokotna oblika je imenovan tudi Standardni obrazec in ga predstavlja (a + ib), kjer sta a in b realni števili.

Na primer: (5 + 5i), (-7i), (-3 – 4i) itd.

Polarna oblika

Polarna oblika je predstavitev kompleksnega števila, kjer so polarne koordinate [kjer so koordinate predstavljene kot (r, θ), kjer je r razdalja od izhodišča in θ je kot med premico, ki povezuje točko in izhodišče ter pozitivno os x) se uporabljajo za predstavitev kompleksnega števila. Vsako kompleksno število je predstavljeno kot r [cos θ + i sin θ].

Na primer: [cos π/2 + i sin π/2], 5[cos π/6 + i sin π/6] itd.

Eksponentna oblika

Eksponentne oblike kompleksnih števil je predstavitev kompleksnih števil z uporabo Eulerjeve formule in v tej obliki je kompleksno število predstavljeno z re^jaz, kjer je r oddaljenost točke od izhodišča in θ kot med pozitivno osjo x in radijskim vektorjem.

Na primer: eⁱ⁽⁰⁾, Je^i(π/2), 5.e^i(π/6)itd.

Opomba: Vse tri zgoraj obravnavane oblike kompleksnih števil so med seboj konvertibilne, kar pomeni, da jih je mogoče zelo enostavno pretvoriti iz ene oblike v drugo.

Operacije s kompleksnimi števili

S kompleksnimi števili je mogoče izvesti naslednje operacije:

• Dodatek
• Odštevanje
• Množenje
• Delitev
• Konjugacija

Seštevanje kompleksnih števil

Dve kompleksni števili lahko seštejemo tako, da ločeno seštejemo njihove realne in imaginarne dele.

Na primer, (3 + 2i) + (1 + 4i) = 4 + 6i.

Odštevanje kompleksnih števil

Dve kompleksni števili lahko odštejemo tako, da ločeno odštejemo njun realni in imaginarni del.

Na primer, (3 + 2i) – (1 + 4i) = 2 – 2i.

Množenje kompleksnih števil

Dve kompleksni števili lahko pomnožimo z uporabo lastnosti distribucije in dejstva, da je i²= -1.

Na primer, (3 + 2i)(1 + 4i) = 3 + 12i + 2i + 8i²= 3 + 14i – 8 = -5 + 14i.

Deljenje kompleksnih števil

Eno kompleksno število lahko delimo z drugim tako, da preprosto pomnožimo števec in imenovalec s kompleksnim konjugatom imenovalca in dodatno poenostavimo izraz.

Na primer, (3 + 2i)/(1 + 4i) = (3 + 2i)(1 – 4i)/(1 + 4i)(1 – 4i) = (11 – 10i)/17.

Konjugacija kompleksnih števil

Z lahkoto najdemo konjugat kompleksnega števila, s preprosto spremembo predznaka njegovega imaginarnega dela. Konjugat kompleksnega števila je pogosto označen s črtico nad številom, na primer z̄.

Na primer, konjugat 3 + 2i je 3 – 2i.

arraylist razvrščena java

Identitete za kompleksna števila

Za kateri koli dve kompleksni števili z₁in z₂lahko podamo naslednje algebraične identitete:

• (Z ₁ + z ₂ ) ² = (z ₁ ) ² + (z ₂ ) ² + 2 z ₁ × z ₂
• (Z ₁ - Z ₂ ) ² = (z ₁ ) ² + (z ₂ ) ² – 2 z ₁ × z ₂
• (Z ₁ ) ² - (z ₂ ) ² = (z ₁ + z ₂ )(Z ₁ - Z ₂ )
• (Z ₁ + z ₂ ) ³ = (z ₁ ) ³ + 3(z ₁ ) ² z ₂ +3(z ₂ ) ² z ₁ + (z ₂ ) ³
• (Z ₁ - Z ₂ ) ³ = (z ₁ ) ³ – 3 (z ₁ ) ² z ₂ +3(z ₂ ) ² z ₁ - (z ₂ ) ³

Formule, povezane s kompleksnimi števili

Obstaja nekaj formul, povezanih s kompleksnimi števili, od katerih so nekatere naslednje:

Eulerjeva formula

Eulerjeva formula prikazuje razmerje med namišljeno potenco eksponenta in trigonometričnim razmerjem sin in cos ter je podana z:

je ^ix = cos x + i sin x

De Moivrejeva formula

De Moivrejeva formula izraža n^thpotenca kompleksnega števila v polarni obliki in je podana z:

(cos x + i sin x) ⁿ = cos(nx) + i sin(nx)

Kompleksna ravnina

Ravnina, na kateri so kompleksna števila edinstveno predstavljena, se imenuje kompleksna ravnina ali Argandova ravnina ali Gaussova ravnina.

Kompleksna ravnina ima dve osi:

• X-os ali Realna os
• Y-os ali imaginarna os

X-os ali Realna os

• Vsa čisto realna kompleksna števila so enolično predstavljena s točko na njem.
• Realni del Re(z) vseh kompleksnih števil je narisan glede nanj.
• Zato se imenuje tudi os X Realna os .

Y-os ali imaginarna os

• Vsa čisto namišljena kompleksna števila so edinstveno predstavljena s točko na njem.
• Imaginarni del Im(z) vseh kompleksnih števil je narisan glede nanj.
• Zato se Y-os tudi imenuje Imaginarna os .

Geometrijska predstavitev kompleksnih števil

Kot vemo, je vsako kompleksno število (z = a + i b) predstavljeno z edinstveno točko p(a, b) na kompleksni ravnini in vsaka točka na kompleksni ravnini predstavlja edinstveno kompleksno število.

Za predstavitev katerega koli kompleksnega števila z = (a + i b) na kompleksni ravnini upoštevajte te konvencije:

• Realni del z (Re(z) = a) postane X-koordinata točke p

• Imaginarni del z (Im(z) = b) postane Y-koordinata točke p

In končno z (a + i b) ⇒ p (a, b), ki je točka na kompleksni ravnini.

Lastnosti kompleksnih števil

Obstajajo različne lastnosti kompleksnih števil, od katerih so nekatere naslednje:

• Za katero koli kompleksno število z = a + ib, če je z = 0, potem je a = 0 kot tudi b = 0.
• Za 4 realna števila a, b, c in d, tako da z₁= a + ib in z₂= c + id. Če z₁= z₂potem je a = c in b=d.
• Seštevanje kompleksnega števila z njegovim konjugatom povzroči čisto realno število, tj. z + z̄ = realno število.

Naj bo z = a + ib,

z + z̄ = a + ena + a – ena

⇒ z + z̄ = 2a (kar je čisto realno)

• Produkt kompleksnega števila z njegovimi konjugiranimi rezultati je prav tako čisto realno število, tj. z × z̄ = realno število

Naj bo torej z = a + ib

z × z̄ = (a + ena) × (a – ena)

⇒ z × z̄= a²- jaz²b²

⇒ z × z̄ = a²+ b²(kar je čisto resnično)

• Kompleksna števila so komutativni pod operacijo seštevanja in množenja. Oglejmo si dve kompleksni števili z₁in z₂, in potem

z ₁ +z ₂ = z ₂ +z ₁

z ₁ × z ₂ = z ₂ × z ₁

• Kompleksna števila so asociativno z operacijo seštevanja in množenja. Oglejmo si tri kompleksna števila z₁, z₂, in z₃potem

(Z ₁ +z ₂ ) +z ₃ = z ₁ + (z ₂ +z ₃ )

(Z ₁ ×z ₂ )×z ₃ = z ₁ ×(z ₂ ×z ₃ )

• Kompleksna števila držijo razdelitvena lastnina množenja tudi nad seštevanjem. Oglejmo si tri kompleksna števila z₁, z₂, in z₃potem

z ₁ ×(z ₂ +z ₃ ) = z ₁ ×z ₂ + z ₁ ×z ₃

Preberi več,

• Deljenje kompleksnih števil
• Z vrstica v kompleksnih številih

Primeri kompleksnih števil

Primer 1: Narišite ta kompleksna števila z = 3 + 2i na kompleksni ravnini.

rešitev:

podano:

z = 3 + 2 i

Torej, točka je z(3, 2). Zdaj to točko narišemo na spodnji graf, tukaj na tem grafu os x predstavlja realni del, os y pa namišljeni del.

Primer 2: Narišite ta kompleksna števila z ₁ = (2 + 2 i), z ₂ = (-2 + 3 i), z ₃ = (-1 – 3 i), z ₄ = (1 – i) na kompleksni ravnini.

rešitev:

podano:

z₁= (2 + 2 i)

z₂= (-2 + 3 i)

z₃= (-1 – 3 i)

z₄= (1 – i)

Torej, točke so z₁(2, 2), z₂(-2, 3), z₃(-1, -3) in z₄(1, -1). Zdaj te točke narišemo na spodnji graf, tukaj na tem grafu os x predstavlja realni del, os y pa namišljeni del.

Pogosta vprašanja o kompleksnih številih

Določite kompleksna števila.

Številom v obliki a+ib pravimo kompleksno število, kjer sta a in b realno število, i pa imaginarna enota, ki predstavlja kvadratni koren iz -1.

Kakšna je razlika med realnim in kompleksnim številom?

Razlika med realnimi in kompleksnimi števili je v tem, da potrebujemo samo eno številko za predstavitev katerega koli realnega števila, vendar potrebujemo dve realni števili za predstavitev katerega koli kompleksnega števila.

Kaj je realni in imaginarni del kompleksnega števila?

V kompleksnem številu a + ib je a realni del kompleksnega števila, b pa se imenuje imaginarni del kompleksnega števila.

dolgo nanizati

Kaj je kompleksni konjugat kompleksnega števila?

Za kompleksno število a + ib se a – ib imenuje njegov kompleksni konjugat. Kompleksne konjugate lahko najdemo tako, da preprosto spremenimo predznak imaginarnega dela.

Kaj je modul kompleksnega števila?

Razdalja med izhodiščem in točko, ki jo predstavlja kompleksno število v argandni ravnini, se imenuje modul tega celotnega števila in je za z = a + ib matematično podana z:

|z| = √(a ² + b ² )

Kaj je argument kompleksnega števila?

Kot med vektorjem radija kompleksnega števila in pozitivno osjo x se imenuje argument kompleksnega števila in je za z = a + ib matematično podan z:

θ = tan ^-1 (b/a)

Kaj je polarna oblika kompleksnega števila?

Za katero koli kompleksno število, z = a + ib, je polarna oblika tega podana z:

r [cos θ + i sin θ]

Kaj je Eulerjeva formula?

Eulerjeva formula prikazuje razmerje med namišljeno potenco eksponenta in trigonometričnim razmerjem sin in cos ter je podana z:

je ^ix = cos x + i sin x