the Kosinusna funkcija ali cos funkcija skratka ena od šestih Trigonometrične funkcije osnova za trigonometrijo. Kosinus je v trigonometriji podan kot razmerje med osnovo in hipotenuzo pravokotnega trikotnika. Kosinusna funkcija je predstavljena kot Cos x, kjer je x kot, za katerega je izračunano kosinusno razmerje. Kar zadeva funkcijo, lahko rečemo, da je x vhod ali domena kosinusne funkcije.

Obširno se uporablja pri številnih predmetih, kot so fizika, geometrija in inženirstvo, med drugim na splošno z izkoriščanjem njegove periodične narave. Uporablja se na primer za definiranje valovne narave zvočnih valov, izračune električnega toka skozi ravno površino itd. V tem članku podrobno izvemo, kaj je kosinusna funkcija, domena in obseg kosinusne funkcije, periodo in graf kosinusne funkcije.

Kazalo

• Kaj je kosinusna funkcija?
• Cos v krogu enote
• Graf kosinusne funkcije
• Inverzna kosinusna funkcija
• Kosinusna funkcija v računu
• Identitete funkcij Cos

Kaj je kosinusna funkcija?

Kosinusna funkcija je trigonometrična funkcija, ki je v osnovi periodične narave. Kosinusna funkcija je izražena kot cos x, kjer je x eden od ostrih kotov pravokotnega trikotnika. Kosinusna funkcija poišče razmerje med osnovo in hipotenuzo za dano vrednost x. Kosinusna funkcija je okrajšana kot cos(x) ali cos(θ), kjer je x kot v radianih in theta θ kot v stopnje na splošno. Kosinusno funkcijo je mogoče definirati z uporabo enotskega kroga, tj. kroga z enotskim polmerom, kot bomo videli kasneje v tem članku. Po naravi je periodičen in ponavlja svoje vrednosti po vsakem popolnem zasuku kotov. Na kartezični ravnini jo lahko imenujemo vektorska komponenta hipotenuze, ki je vzporedna z osjo x.

Definicija kosinusne funkcije

Kosinusna funkcija je definirana v pravokotnem trikotniku kot razmerje med dolžino stranice, ki meji na zadevni kot, in dolžino hipotenuze. Matematično je kosinusna funkcija podana kot

Cos x = Cos θ = dolžina osnove/dolžina hipotenuze = b/h = OB/OA

kje x je kot v radianih in θ je enakovredni kot v stopinjah.

Domena in območje funkcije Cos

Vemo, da je za funkcijo domena dovoljene vhodne vrednosti, obseg pa izhodna vrednost za določeno vhodno ali domensko vrednost. Zato lahko domnevamo, da funkcija deluje kot procesor, ki sprejema vhodne podatke, jih obdela in daje določen izhod. Domena in obseg funkcije cos sta obravnavana spodaj:

• Domena kosinusne funkcije: R tj. množica vseh realnih števil.
• Razpon kosinusne funkcije: [-1, 1], tj. izhod se razlikuje med vsemi realnimi števili med -1 in 1.

Perioda kosinusne funkcije

The funkcijo je periodične narave, tj. ponavlja se po 2π ali 360°. Z drugimi besedami, ponovi se po vsaki popolni rotaciji. Zato je obdobje kosinusne funkcije popolna rotacija ali kot 360° (ali 2π).

Recipročna vrednost kosinusne funkcije

Recipročna vrednost kosinusne funkcije je znana kot sekant funkcijo oz sek na kratko. Matematično je recipročna vrednost kosinusne funkcije podana kot

kamelji piton

sec(θ) = 1/cos(θ)

V skladu s pravili Vzajemne vrednosti , če pomnožimo Cos x s Sec x, bo produkt vedno 1.

Graf kosinusne funkcije

Graf kosinusne funkcije je podoben grafu sinusne funkcije z osnovno razliko, da pri x = 0 gre graf sinusne funkcije iz izhodišča, medtem ko pri x = 0 gre graf kosinusne funkcije iz (0, 1) na osi y. Sledi graf vrednosti kosinusne funkcije, tj. y = cos x

Zgoraj obravnavane lastnosti je mogoče videti na grafu, kot je periodična narava funkcije.

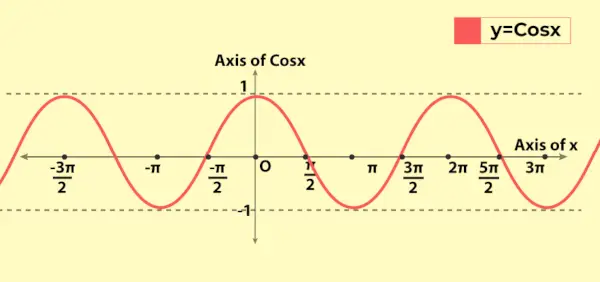
Variacija kosinusne funkcije v grafu

Ker je obseg kosinusne funkcije [-1, 1], se na grafu spreminja od -1 do 1. Kaže svojo periodično naravo, ko se graf ponovi po vsaki dolžini 2π na osi x. To odraža, da ima kosinusna funkcija periodo 2π (ali 360°).

Cos v krogu enote

Kosinusno funkcijo je mogoče definirati z uporabo enotskega kroga. Razumejmo, kako lahko definiramo kosinusno funkcijo v smislu enotskega kroga.

Razmislite o odseku OA, ki se vrti okoli točke O, kjer je O izhodišče kartezične ravnine. Tako rotacija OA opisuje enotski krog (krog enotskega polmera) s središčem v izhodišču O in točka A vedno leži na tem krogu. Če spustimo navpičnico iz A na os x in točko presečišča imenujemo B, θ pa je kot, ki ga OA tvori s pozitivno smerjo osi x, potem je cos(θ) = projekcija hipotenuze na x -os = OB/|OA| = OB (ker je |OA| = 1 enota).

Upoštevajte, da je smer OB pomembna, kot je razvidno iz naslednjih slik. Zeleni segment označuje dolžino/magnitudo, puščica pa smer (+ve ali -ve) cos(θ)

Upoštevajte, da je vrednost cos(θ) pozitivna za θ, ki pripada prvemu in četrtemu kvadrantu, medtem ko je negativna za θ, ki pripada drugemu in tretjemu kvadrantu.

Inverzna kosinusna funkcija

Inverzna funkcija kosinusa, znana kot ark-kosinus funkcijo in skrajšano kot arccos(x) oz cos ^-1 (x) je definiran kot sledi

cos(x) = y

⇒ cos ^-1 (y) = x

Domena in območje inverzne kosinusne funkcije

Domena in obseg inverzne kosinusne funkcije sta navedena spodaj:

• Domena inverzne kosinusne funkcije: Vsa realna števila v območju [-1, 1]
• Razpon inverzne kosinusne funkcije: Vsa realna števila v območju [0, π]

Hiperbolična kosinusna funkcija

Hiperbolične funkcije so analogni ekvivalent trigonometrične funkcije, katere algebraični izraz je v smislu eksponentne funkcije. Hiperbolična kosinusna funkcija, skrajšano kot cosh(x) kje x je hiperbolični kot je koncept hiperbolične geometrije. Tako kot (cos(x), sin(x)) predstavlja točko na enotskem krogu, (cosh(x), sinh(x)) predstavlja točko na enotski hiperboli, tj. xy = 1, kjer sinh(x) predstavlja hiperbolično sinusna funkcija. Algebraična ekspanzija hiperbolične funkcije cos je podana kot

cosh(x) = (e ^x + in ^-x )/2

Več podrobnosti o hiperboličnih funkcijah je izven obsega tega članka, vendar se lahko obrnete na njih Ta članek .

Kosinusna funkcija v računu

Veja računanja v matematiki se ukvarja z diferenciacijo in integracijo dane funkcije. Diferenciacija funkcije je stopnja spremembe funkcije glede na neodvisno spremenljivko, medtem ko je integracija obratni proces diferenciacije, ki se ukvarja z iskanjem integrala funkcije, katere odvod obstaja.

Odvod kosinusne funkcije

The izpeljanka kosinusne funkcije je enako minus sinusne funkcije. Matematično

d(cos(x))/dx = -sin(x)

Integracija kosinusne funkcije

The nedoločen integral kosinusne funkcije je enaka sinusni funkciji. Matematično –

∫cos(x)dx = sin(x) + C, kjer je C konstanta integracije.

Sinusne in kosinusne funkcije

Naslednji graf predstavlja ključno razliko med sinusno in kosinusno funkcijo:

Razlika med sinusno in kosinusno funkcijo

Naslednja tabela navaja razlike med sinusno in kosinusno funkcijo –

Tabela vrednosti Cos

Naslednja tabela podaja vrednosti kosinusne funkcije za nekatere skupne kote v prvem kvadrantu kartezične ravnine –

Z uporabo teh vrednosti lahko enostavno izračunamo vrednosti drugih običajnih kotov, kot so 15°, 75°, 195°, -15° itd., z uporabo formul cos (x + y) in cos (x – y), opisanih kasneje v tem Članek.

Preverite, Trigonometrična tabela

Identitete funkcij Cos

Osnovne trigonometrične identitete, povezane s kosinusno funkcijo, so navedene spodaj:

• brez²(x) + cos²(x) = 1
• cos(x + y) = cos(x)cos(y) – sin(x)sin(y)
• cos(x – y) = cos(x)cos(y) + sin(x)sin(y)
• cos(-x) = cos(x)
• cos(x) = 1/s(x)
• cos 2x = cos²x – greh²x = 1 – 2sin²x = 2cos²x – 1 = (1 – tan²x/1 + tan²x)
• cos 3x = 4cos³x – 3cos x

povezani članki

• Diferenciacija trigonometričnih funkcij
• Inverzne trigonometrične funkcije
• Inverzni trigonski izpeljanki

Rešeni primeri kosinusne funkcije

Tukaj je nekaj rešenih primerov, ki vam bodo pomagali bolje razumeti koncept kosinusne funkcije.

Primer 1: Kakšne so največja in najmanjša vrednost kosinusne funkcije?

rešitev:

Največja vrednost kosinusne funkcije je 1 pri 0° in 180°, medtem ko je najmanjša vrednost funkcije -1 pri 180°.

Primer 2: Pri katerih kotih v območju [0, 360] je vrednost kosinusne funkcije 0?

rešitev:

Vrednost kosinusne funkcije je 0 pri kotih 90° in 270°.

Primer 3: Za katere kvadrante je vrednost kosinusne funkcije negativna?

rešitev:

Kosinusna funkcija je negativna v II^ndin III^rdkvadrantih.

Primer 4: Izračunajte vrednost cos (45°).

rešitev:

pvr polna oblika

Glede na zgoraj navedeno identiteto 4 je cos(-x) = cos(x).

Zato je cos(-45°) = cos(45°) = 1/√2

Primer 5: Izračunajte vrednost cos(15°).

rešitev:

Uporaba zgoraj navedene identitete 3 –

cos(15degree) = cos(45degree – 30degree) ewline = cos(45degree)cos(30degree) + sin(45degree)sin(45degree) ewline = frac{1}{sqrt2} imesfrac{sqrt3}{2} + frac{1}{sqrt2} imes frac{1}{2} ewline = frac{sqrt3 + 1}{2sqrt2}

Primer 6: Kaj je cos ^-1 (1/2) v območju [0,π]?

rešitev:

Naj cos^-1(1/2) = y.

Zato je cos(y) = 1/2 ⇒ y = π/3 v zgornjem danem območju.

Torej je odgovor π/3.

Primer 7: Kakšna je vrednost cos(-15°)?

rešitev:

Uporaba zgoraj navedene identitete 3 –

cos(-15degree) ewline = cos(30degree – 45degree) ewline = cos(30degree)cos(45degree) + sin(30degree)sin(45degree) ewline = frac{sqrt3}{2} imesfrac{1}{sqrt{2}} + frac{1}{2} imesfrac{1}{sqrt2} ewline = frac{sqrt3 + 1}{2sqrt2} .

Lahko pa uporabimo tudi identiteto cos(-x) = cos(x) in uporabimo vrednost cos(15°), izračunano v primeru 5.

Primer 8: Izračunajte ploščino pod grafom kosinusne funkcije za x = 0 do x = π/2.

rešitev:

Dano površino je mogoče izračunati z rešitvijo naslednjega določenega integrala –

int_0^{frac{pi}{2}}cos(x)dx ewline = sin(frac{pi}{2}) – sin(0) ewline = 1 – 0 ewline = 1

Zato je odgovor 1 kvadratna enota.

Primer 9: Če je cos(x) = π/3, poiščite vrednost cos(3x) (v decimalni obliki z natančnostjo dveh decimalnih mest).

rešitev:

Uporaba identitete – cos(3x) = 4cos³(x) – 3cos(x) –

cos(3x) = 4⨉(π/3)³-3⨉(π/3) ≅ 4,59 – π = 1,45

Primer 10: Poiščite vrednost cos(120°).

rešitev:

Uporaba identitete za cos(2x)

cos(120°) = cos(2⨉60°) = 1 – 2 sin²(60°) = 1- 2⨉(√3/2)²= 1 – 3/2 = -1/2

Vprašanja za vajo: Funkcije Cos

Q1. Kakšna je formula za izračun cos kota v pravokotnem trikotniku?

Q2. Kakšna je geometrijska interpretacija cos na kartezični ravnini?

Q3. Izračunajte vrednost cos(120°).

Q4. Poiščite vrednost cos ^-1 (√3/2) v območju [π, 2π].

V5. Če palica meče senco enake dolžine na tla, poiščite kot sonca glede na tla, če je sonce v vzhodni smeri.

Povzetek – kosinusna funkcija

Kosinusna funkcija, označena kot cos(x), je temeljna trigonometrična funkcija, definirana kot razmerje med osnovo in hipotenuzo v pravokotnem trikotniku in je zaradi svoje periodične narave bistvena na različnih področjih, kot so fizika, inženiring in geometrija. , ki je ključnega pomena pri modeliranju vedenja valov. Ima domeno vseh realnih števil in obseg od -1 do 1, pri čemer se svoj cikel ponavlja vsaki 2 Pi radianov ali 360 stopinj, kar je razvidno iz njegovega valovitega grafa, ki se začne pri (0,1). V smislu računa je odvod cos(x) − sin( x ), njegov integral pa daje sin( x )+ C , s C kot konstanto integracije. Ta funkcija se razširi tudi na hiperbolične oblike, kot je cosh(x), kar izboljša njeno uporabo v različnih matematičnih kontekstih in rešitvah, vključno z izračuni valov in nihanji v fizičnih sistemih.

Kosinusna funkcija: pogosta vprašanja

1. Kaj je kosinusna funkcija?

Kosinusna funkcija je ena temeljnih trigonometričnih funkcij. V pravokotnem trikotniku je definiran kot razmerje med dolžino stranice, ki meji na zadevni kot, in dolžino hipotenuze.

2. Ali sta cos in kosinus enaka v trigonometriji?

ja cos je okrajšava/kratka oblika kosinusne funkcije.

3. Kaj je obseg funkcije Cos?

Razpon funkcije cos ali kosinusa so vsa realna števila v razponu od -1 do 1, tj. [-1,1].

4. Kaj je domena funkcije Cos?

Domena funkcije cos ali kosinusa je ser vseh realnih števil, tj. R .

5. Kakšna je največja vrednost kosinusne funkcije?

Največja vrednost kosinusne funkcije je 1 za vse kote, enakovredne 0° ali 360°.

6. Kakšna je najmanjša vrednost kosinusne funkcije?

Najmanjša vrednost kosinusne funkcije je -1 za vse kote, enakovredne 180°.

7. Kako najti vrednost Cos(-x)?

Vrednost cos(-x) je mogoče izračunati z izračunom vrednosti cos(x) zaradi obstoja naslednje identitete: cos(-x) = cos(x).

8. Kako narisati graf kosinusne funkcije?

Če želite narisati graf kosinusne funkcije na kartezični ravnini, uporabite os x, ki predstavlja kote v radianih (ali stopinjah), in os y, ki predstavlja vrednosti kosinusne funkcije za ustrezni kot na osi x. zdaj,

• Korak 1: Vzemite podmnožico osi x, za katero želite narisati graf.
• 2. korak: Razdelite os x v tem obsegu na enako oddaljene točke (tj. med vsemi podtočkami je enak prostor). Upoštevajte, da večje kot je število delitev, večja je natančnost rezultantnega grafa.
• 3. korak: Za vsako od teh podtočk x označite točko (x, cos(x)) na grafu.
• 4. korak: Združite vse označene točke, da dobite graf kosinusne funkcije (za izbrano podmnožico osi x).

9. Kako najti periodo kosinusne funkcije?

Perioda kosinusne funkcije se nanaša na najmanjši obseg vrednosti, po katerem se funkcija začne ponavljati. Vemo, da se kosinusna funkcija ponovi po vsakem popolnem obratu, kar pomeni 2π radiana. Zato je perioda kosinusne funkcije 2π radiana ali 360°.

10. Kaj je amplituda kosinusne funkcije?

Amplituda kosinusne funkcije se nanaša na največji odmik vrednosti funkcije od srednjega položaja, tj. osi x. Amplituda kosinusne funkcije je 1, saj je največji premik 1 (za vrednosti -1 in 1 pri 180 oziroma 0 stopinjah. Upoštevajte, da je obseg kosinusne funkcije [-amplituda, amplituda].