Kot se meri v stopinjah (°) in radianih. Nastane med dvema sosednjima stranicama mnogokotnika. Vsak mnogokotnik ima različne stranice in različno število kotov. Formula za iskanje kotov v stopinjah je uporabna v geometriji in trigonometriji. Bistveno je razumeti druge pojme matematike, kot so lok, središčni kot kroga itd.
- Poln krog = 360°
- Ravna črta = 180°
- Polkrog = 180°
- Četrtina kroga = 90°
Računanje kotov v stopinjah
Obstajajo trije različni načini iskanja kotov v stopinjah, ki so naslednji:
- Uporaba zaščite D
- Uporaba Pitagorovega izreka in trigonometrične funkcije v pravokotnem trikotniku
- Uporaba formule za vsoto kotov
- Osrednji kot kroga
Uporaba zaščite D
Ščitnik je vrsta ravnila ali tehtnice, ki se uporablja za merjenje razdalje v centimetrih ali milimetrih. Zaščita, ki se uporablja za merjenje kotov, je v obliki črke 'D' z vrednostjo kotov, označeno od 0 do 180 ° iz katere koli smeri (desno ali levo). Za merjenje kota moramo os poravnati s črto na D. Srednji krog zaščite je poravnan z vrhom merjenega kota. Žarki vzdolž vrha kota bodo pomagali najti kot v stopinjah.
Uporaba Pitagorovega izreka in trigonometrične funkcije v pravokotnem trikotniku
V trigonometriji je šest funkcij, sinus, cos, cosec, tan, cot, in sek. Pravokotni trikotnik ima tri stranice, osnovo, pravokotnik in hipotenuzo.
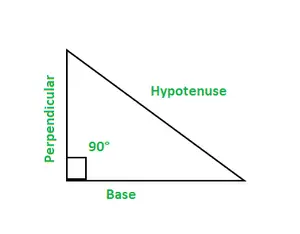
- Osnova: Je sosednja stranica na kot 90°. Navpičnica: Je tudi sosednja stranica na kot 90°. Hipotenuza: Je stranica, ki je nasprotna kotu 90°.
Pravokotni trikotnik je kot eden od kotov predstavljen s kotom 90°. Skupna vsota kotov trikotnika je 180°.
- Cosecθ: Predstavljen je kot hipotenuza, deljena s pravokotnico.
Cosecθ =
- Cotθ: Predstavljen je kot osnova, deljena z navpičnico.
Cotθ =
Druge trigonometrične funkcije so predstavljene kot:
sinθ =
Cosθ =
kako razkriti skrite aplikacijetanθ =
secθ =
Cosecθ je lahko predstavljen tudi kot 1/ sinθ
secθ lahko predstavimo tudi kot 1/ cosθ
Cotθ je lahko predstavljen tudi kot 1/tanθ
Kje,
Θ je kot
Pitagorov izrek
Če poznamo dve strani pravega kota, zlahka izračunamo tretjo stran pravokotnega trikotnika. V pravokotnem trikotniku je Pitagorov izrek podan z:
(hipotenuza)2= (Osnova)2+ (pravokotno)2
Formula vsote kotov
Vsota kotov se nanaša na skupno vsoto notranjih kotov mnogokotnika, ki se tvori med obema stranicama. Če je v mnogokotniku šest stranic, je okoli šest kotov. Pomaga pri iskanju kota, če so znani drugi koti in vsota kotov mnogokotnika.
Formula za iskanje skupne vsote kotov mnogokotnika je podana z:
Skupna vsota kotov = 180 (n – 2)
Kje,
n je število stranic mnogokotnika
primer:
- Če je n = 4,

Skupna vsota kotov = 180 (4 – 2)
= 180 (2)
= 360°
Če je n = 5,
Skupna vsota kotov = 180 (5 – 2)
= 180 (3)
= 540°
- Če je n = 6

Skupna vsota kotov = 180 (6 – 2)
= 180 (4)
= 720°
Osrednji kot kroga
Krog je okrogla oblika, katere meja je enako oddaljena od njegovega središča. Razdalja med središčem in mejo je znana kot polmer kroga. Kot, ki ga tvorita polmera kroga, je znan kot središčni kot. Vrednost središčnega kota kroga je med 0 in 360 stopinjami.

Formula za izračun središčnega kota kroga je podana z:
Dolžina loka = 2πr × (θ/360)
Θ = 360L/2 pr
Kje,
r je polmer kroga
AB je lok
Theta je kot v stopinjah.
L = dolžina loka
Vzorčne težave
Vprašanje 1: Poiščite središčni kot kroga s polmerom 2 m z lokom dolžine 4 m?
rešitev :
Formula za izračun središčnega kota kroga je podana z:
Θ = 360L/2pr
Kje,
r je polmer kroga
Theta je kot v stopinjah.
L = dolžina loka
Θ = kot v stopinjah
r = 2m
L = 4m
Θ = 360 × 4 /2 × π × 2
Θ = 114,6°
Tako je središčni kot kroga 114,6°.
2. vprašanje: Poiščite središčni kot kroga s polmerom 10 cm in lokom dolžine 18 cm?
rešitev :
Formula za izračun središčnega kota kroga je podana z:
Θ = 360L/2 pr
Kje,
r je polmer kroga
Theta je kot v stopinjah.
L = dolžina loka
r = 10 cm
L = 18 cm
Θ = kot v stopinjah
Θ = 360 × 18 /2 × π × 10
Θ = 103,13°
Tako je središčni kot kroga 103,13°.
3. vprašanje: Poiščite kot paralelograma, če so ostali trije koti 80°, 95° in 105°?
rešitev :
V paralelogramu so štiri stranice s skupno vsoto kotov 360°.
Formula za iskanje vsote kotov = 180 (n – 2)
Kje,
n je število stranic mnogokotnika
Tukaj je n = 4,
Skupna vsota kotov = 180 (4 – 2)
= 180 (2)
= 360°
Skupna vsota = kot 1 + kot 2 + kot 3 + kot 4
360 = 80+ 95+ 105+ 4. kot
360 = 280 + kot 4
Kot 4 = 360 – 280
Kot 4 = 80°
4. vprašanje: Poiščite kot A na podani sliki.

rešitev :
Podano: hipotenuza = 12
Pravokotno = 6
Trigonometrična funkcija za izračun kota je podana z:
koliko mest v Združenih državah AmerikesinA = 6/12
A = 30°
5. vprašanje: Poiščite kot A na dani sliki.

rešitev :
Podano: hipotenuza = 10
Osnova = 5
Trigonometrična funkcija za izračun kota je podana z:
CosA = 5/10
A = 60°
6. vprašanje: Poiščite kot peterokotnika, če so drugi štirje koti 115°, 100°, 105° in 100°?
rešitev :
V peterokotniku je pet stranic s skupno vsoto kotov 540°.
Formula za iskanje vsote kotov = 180 (n – 2)
Kje,
n je število stranic mnogokotnika
Tukaj je n = 5,
Skupna vsota kotov = 180 (5 – 2)
= 180 (3)
= 540°
Skupna vsota = kot 1 + kot 2 + kot 3 + kot 4 + kot 5
540 = 115° + 100° + 105°+100° + kot 5
540 = 420 + kot 5
Kot 5 = 540 – 420
Kot 5 = 120°
7. vprašanje: Poiščite kot A na podani sliki.

rešitev :
Podano: osnova = √3
Pravokotno = 1
Trigonometrična funkcija za izračun kota je podana z:
tanθ =
tanθ = 1/√3
A = 30°
8. vprašanje: Poiščite kot paralelograma, če so drugi trije koti 100°, 70° in 80°?
rešitev :
V paralelogramu so štiri stranice s skupno vsoto kotov 360°.
Formula za iskanje vsote kotov = 180 (n – 2)
Kje,
n je število stranic mnogokotnika
Tukaj je n = 4,
Skupna vsota kotov = 180 (4 – 2)
= 180 (2)
= 360°
Skupna vsota = kot 1 + kot 2 + kot 3 + kot 4
360 = 100 + 70 + 80 + kot 4
360 = 250 + kot 4
Kot 4 = 360 – 250
Kot 4 = 110°
Tako je drugi kot 110°.
Vprašanje 9: Poiščite kot šesterokotnika, če je ostalih pet kotov 120°, 115°, 110°, 125° in 105°?
rešitev :
V šesterokotniku je šest stranic s skupno vsoto kotov 720°.
Formula za iskanje vsote kotov = 180 (6 – 2)
Kje,
n je število stranic mnogokotnika
Tukaj je n = 6,
Skupna vsota kotov = 180 (6 – 2)
= 180 (4)
= 720°
Skupna vsota = kot 1 + kot 2 + kot 3 + kot 4 + kot 5 + kot 6
720 = 120 + 115 + 110 + 125 + 105 + kot 6
720 = 575 + kot 6
Kot 6 = 720 – 575
Kot 6 = 145°
Torej je šesti kot šestkotnika 145°.






