FORMULA KOTANGENSA

Trigonometrija je pomembna veja matematike, ki se ukvarja z razmerjem med dolžinami stranic in koti pravokotnega trikotnika. Sinus, kosinus, tangens, kosekans, sekans in kotangens je šest trigonometričnih razmerij ali funkcij. Kjer je trigonometrično razmerje prikazano kot razmerje med stranicami pravokotnega trikotnika.

sin θ = nasprotna stran/hipotenuza
cos θ = sosednja stranica/hipotenuza
tan θ = nasprotna stran/sosednja stran
cosec θ = 1/sin θ = hipotenuza/nasprotna stran
sec θ = 1/cos θ = hipotenuza/sosednja stranica
posteljica θ = 1/tan θ = sosednja stran/nasprotna stran

Funkcija kotangens je recipročna funkcija dane funkcije tangensa. Vrednost kotangensa kota v pravokotnem trikotniku je razmerje med dolžino stranice, ki meji na dani kot, in dolžino stranice, ki je nasproti danemu kotu. Funkcijo kotangens zapišemo kot cot.

Trikotnik ABC

Formula kotangensa za kot θ je,

posteljica θ = (sosednja stran)/(nasprotna stran)

Kotangens je pozitiven v prvem in tretjem kvadrantu ter negativen v drugem in četrtem kvadrantu.

posteljica (2π + θ) = posteljica θ (1^stkvadrant)
posteljica (π – θ) = – posteljica θ (2^ndkvadrant)
posteljica (π + θ) = posteljica θ (3^rdkvadrant)
posteljica (2π – θ) = – posteljica θ (4^thkvadrant)

Kotangens je negativna funkcija, saj je kotangens negativnega kota minus kotangensa pozitivnega kota.

posteljica (-θ) = – posteljica θ

V smislu funkcije tangensa je funkcija kotangens zapisana kot

posteljica θ = 1/tan θ

(ali)

cot θ = tan (90° – θ) (ali) tan (π/2 – θ)

Funkcijo kotangens v smislu funkcij sinusa in kosinusa lahko zapišemo kot

cot θ = cos θ/sin θ
java break

To vemo, posteljica θ = sosednja stran/nasprotna stran

Zdaj delite števec in imenovalec s hipotenuzo

⇒ posteljica θ = (sosednja stranica/hipotenuza) / (nasprotna stran/hipotenuza)

Vemo, da je sin θ = nasprotna stran/hipotenuza

cos θ = sosednja stranica/hipotenuza

Zato je cot θ = cos θ/sin θ

Funkcijo kotangens v smislu sinusne funkcije lahko zapišemo kot,

cot θ = (√1 – sin ² i)/greh i

Vemo, da je cot θ = cos θ/sin θ

Iz pitagorejskih identitet imamo;

cos²θ + sin²θ = 1

⇒ cos θ = √1 – sin²jaz

Zato je cot θ = $frac{sqrt{left(1-sin^{2} hetadesno)}}{sin heta}$

Funkcijo kotangens v smislu kosinusne funkcije lahko zapišemo kot

cot θ = cos θ/(√1 -cos ² jaz)

Vemo, da je cot θ = cos θ/sin θ

Iz pitagorejskih identitet imamo;

cos²θ + sin²θ = 1

sin θ = √1 – cos²jaz

Zato je cot θ = $frac{cos heta}{sqrt{left(1-cos^{2} hetadesno)}}$

Funkcijo kotangens v smislu funkcij sekansa in kosekansa lahko zapišemo kot,

cot θ = cosec θ/sec θ

Imamo cot θ = cos θ/sin θ

To lahko zapišemo kot cot θ = (1/sin θ) / (1/cos θ)

⇒ cot θ = cosec θ/sec θ

Funkcijo kotangens v smislu funkcije kosekansa lahko zapišemo kot:

cot θ = √(cosec ² - 1)

Iz pitagorejskih identitet imamo,

cosec²θ – posteljica²θ = 1

⇒ posteljica²θ = 1 – cosec²- 1

Zato je cot θ = √(cosec²- 1)

Funkcijo kotangens v smislu funkcije sekansa lahko zapišemo kot:

posteljica θ = 1/(√sek ² i – 1)

Iz pitagorejskih identitet imamo,

sek²θ – torej²θ = 1

tan θ = √sek²i – 1

Vemo, da je cot θ = 1/tan θ

torej posteljica θ = $frac{1}{sqrt{left(1-sec^{2} hetadesno)}}$

Tabela trigonometričnega razmerja

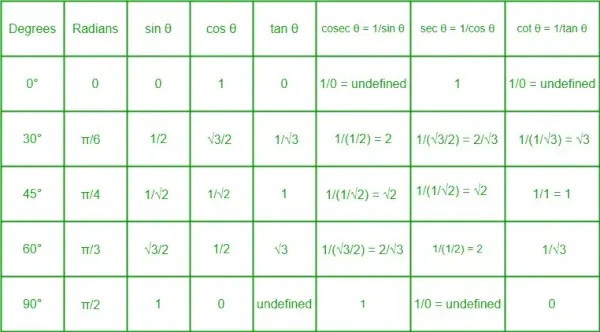
Tabela trigonometričnega razmerja

Kotangensov zakon ali kotangensov zakon

Kotangensov zakon je podoben sinusnemu zakonu, vendar tukaj vključuje polovične kote. Zakon kotangensov opisuje razmerje med dolžinami stranic trikotnika in kotangensi polovic treh kotov. Vzemimo trikotnik ABC, kjer so a, b in c dolžine stranic trikotnika.

Zakon kotangensov pravi, da

$frac{cot(frac{A}{2})}{(s-a)} = frac{cot(frac{B}{2})}{(s-b)} = frac{cot(frac{ C}{2})}{(s-c)} = frac{1}{r}$

Kjer je s polobseg trikotnika ABC in r njegov notranji polmer včrtane krožnice trikotnika.

s = (a + b + c)/2

r = $sqrt{frac{(s-a)(s-b)(s-c)}{s}}$

Vzorčne težave

Problem 1: Poiščite vrednost cot θ, če je tan θ = 3/4.

rešitev:

Glede na podatke je tan θ = 3/4

Vemo, da posteljica θ = 1/tan θ

⇒ posteljica θ = 1/(3/4) = 4/3

Torej, posteljica θ = 4/3

2. naloga: Poiščite vrednost cot α, sin α = 1/3 in cos α = 2√2/3.

testiranje in vrste programske opreme

rešitev:

Glede na podatke je sin α = 1/3 in cos α = 2√2/3

Vemo, da cot α = cos α/sin α

⇒ posteljica α = (2√2/3) / (1/3) = 2√2

Zato je vrednost cot α = 2√2

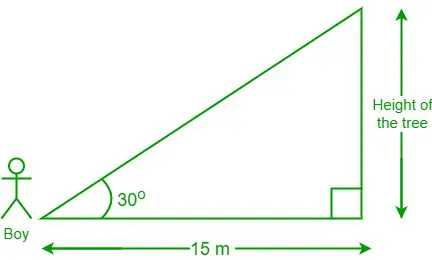
3. problem: Fant, ki stoji 15 m od drevesa, gleda pod kotom 30 stopinj na vrh drevesa. Kakšna je višina drevesa?

rešitev:

Diagram iz podanih podatkov

Glede na podatke je razdalja med dečkom in vznožjem drevesa = 15 m in θ = 30°

Naj bo višina drevesa 'h'

Imamo, posteljica θ = sosednja stran/nasprotna stran

⇒ posteljica 30° = 15/h

⇒ √3 = 15/h [ker je posteljica 30° = √3]

⇒ h = 15/√3

⇒ h = 5√3 m

Torej je višina drevesa = 5√3 m

Problem 4: Poiščite vrednost cot x, če je sec x = 6/5.

rešitev:

Podani podatki, sec x = 6/5

Imamo, sek ² x – torej ² x = 1

⇒ (6/5)²- torej²x = 1

⇒ 36/25 – torej²x = 1

⇒ torej²x = 36/25 – 1

⇒ torej²x = 11/25

⇒ tan x = √(11/25) = √11/5

Vemo, da otroška posteljica x = 1/tan x

⇒ posteljica x = 1/(√11/5) = 5/√11

Zato je cot x = 5/√11

Problem 5: Poiščite vrednost cot θ, če je cosec θ = 25/24.

rešitev:

Podani podatki, cosec θ = 25/24

Vemo, da cot θ = √(cosec ² - 1)

⇒ posteljica θ = √(25/24)²- 1

⇒ posteljica θ =√(625 – 576)/576 = √49/576

⇒ posteljica θ = 7/24

Zato je vrednost cot θ = 7/24

Problem 6: Poiščite vrednost cot β, če je sin β = 5/13.

rešitev:

Podani podatki, sin β = 5/13

Vemo, da brez ² β + cos ² β = 1

⇒ (5/13)²+ cos²β = 1

⇒ cos²β = 1 – (5/13)²= 1 – 25/169 = 144/169

⇒ cos β = √144/169 = 12/13

cot β = cosβ/sin β

= (12/13) / (5/13)

⇒ posteljica β = 12/5

Zato je vrednost cot β = 12/5

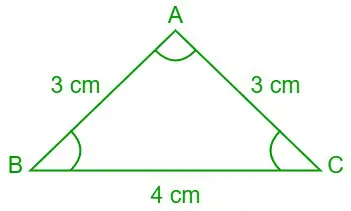
7. naloga: Z uporabo zakona kotangensov poiščite vrednosti ∠A, ∠B in ∠C (v stopinjah), če so dolžine treh stranic trikotnika ABC a = 4 cm, b= 3 cm in c= 3 cm.

rešitev:

Podano je a = 4 cm, b = 3 cm in c = 3 cm

Trikotnik ABC

Iz kotangensnega zakona,

$frac{cot(frac{A}{2})}{(s-a)} = frac{cot(frac{B}{2})}{(s-b)} = frac{cot(frac{ C}{2})}{(s-c)} = frac{1}{r}$

s = (a + b + c)/2

⇒ s = (3 + 4 + 3)/2 = 10/2 = 5

Zdaj je s – a = 5 – 4 = 1

⇒ s – b = 5 – 3 = 2

⇒ s – c = 5 – 3 = 2

r = $sqrt{frac{(s-a)(s-b)(s-c)}{s}}$

⇒ r = √[(1)(2)(2)/5]

Polmer trikotnika r = 2/√5

Iz enačbe zakona kotangensov,

posteljica (A/2)/1 = 1/(2/√5)

⇒ otroška posteljica (A/2) = √5/2 ⇒ A/2 = otroška posteljica^-1(√5/2)

⇒ (A/2) = 41,8° ⇒ ∠A = 83,6°

posteljica (B/2)/2 = 1/(2/√5)

⇒ otroška posteljica (B/2)/2 = √5/2 ⇒ otroška posteljica (B/2) = √5

⇒ (B/2) = otroška posteljica^-1(√5) = 24,1° ⇒ ∠B = 48,2°
arp - ukaz

posteljica (C/2)/2 = 1/(2/√5)

⇒ posteljica (C/2) = √5 ⇒ (C/2) = posteljica^-1(√5)

⇒ (C/2) = 24,1° ⇒ ∠C = 48,2°

Torej so koti trikotnika ABC ∠A = 83,6°, ∠B = 48,2° in ∠C = 48,2°.