A funkcija v matematiki je posebna relacija med množico vhodnih vrednosti in množico izhodnih vrednosti. V funkciji daje vsaka vhodna vrednost določeno izhodno vrednost. Funkcijo v matematiki predstavljamo kot y = f(x), kjer je x je vhodna vrednost in za vsako x dobimo izhodno vrednost kot y.

V tem članku bomo spoznali, funkcije v matematiki, njihove različne vrste, primeri in drugo podrobno.

top 10 hentai

Kazalo

• Kaj je funkcija v matematiki?
• Definicija funkcije v matematiki
• Primeri funkcij
• Pogoj za funkcijo
• Predstavitev funkcij v matematiki
• Identifikacija funkcije
• Vrste funkcij
• Kaj je funkcija v algebri?
• Domena in obseg funkcije
• Sestava funkcij
• Algebra funkcij
• Kaj je funkcija na grafu?
• Grafične funkcije
• Skupne funkcije
• Uporaba funkcij
• Primeri o funkciji
• Vadite naloge o tem, kaj je funkcija

Kaj je funkcija v matematiki?

Funkcija v matematiki je a odnos med vhodnimi vrednostmi (domena) in izhodnimi vrednostmi (obseg) danih nizov tako, da dve spremenljivki iz domenskih nizov nista povezani z isto spremenljivko v nizu obsega. Preprost primer funkcije v matematiki je f(x) = 2x, ki je definirana na R→R, pri čemer je katera koli spremenljivka v domeni povezana samo z eno spremenljivko v območju.

Funkcija v matematiki ima domeno, kodomeno in obseg. Domena je množica vseh možnih vrednosti x, obseg funkcije pa množica vseh izhodnih vrednosti y. Obseg je podmnožica kodomene funkcije. Lahko tudi rečemo, da je funkcija v matematiki relacija z edinstvenim izhodom in nobeni dve vhodni vrednosti nimata podobnega izhoda v funkciji, kar velja za relacijo.

Definicija funkcije v matematiki

Funkcija je posebna relacija ali metoda, ki povezuje vsakega člana množice A z edinstvenim članom množice B prek definirane relacije. Množica A se imenuje domena, množica B pa sodomena funkcije. Funkcija v matematiki od množice A do množice B je definirana kot,

f = ∀ a ∈ A, b ∈ B

Vsaka funkcija je relacija, vendar vsaka relacija ni funkcija. Kriteriji, da se katera koli relacija šteje za funkcijo, saj ima v funkciji vsak element množice A samo eno sliko v množici B, medtem ko ima lahko v relaciji element množice A več kot eno sliko v množici B.

V matematiki definiramo funkcije od neprazne množice A do neprazne množice B tako, da

(a, b) ∈ f, potem je f(a) = b

kamor smo poklicali b kot podoba a definiran pod relacijo f .

Vsak element 'a' množice A ima edinstveno sliko ' b ' v množici B, potem je to funkcija.

Primeri funkcij

Funkcija v matematiki f je definirana kot y = f(x), kjer je x je vhodna vrednost in za vsako vhodno vrednost x dobimo edinstveno vrednost y. Različni primeri funkcij v matematiki, definiranih na R→R, so,

• y = f(x) = 3x + 4
• y = f(x) = sin x + 3
• y = f(x) = -3x²+ 3 itd

Pogoj za funkcijo

Za kateri koli dve neprazni množici A in B funkcija f: A→B označuje to f je funkcija od A do B, kjer je A je domena in B je sodomena.

Za vsak element, a ∈ A, obstaja edinstven element b ∈ B, tako da (a,b) ∈ f. Edinstveni element b, ki je povezan z a, je označen s f(a) in se bere kot f od a. To je mogoče bolje razumeti iz spodnje slike:

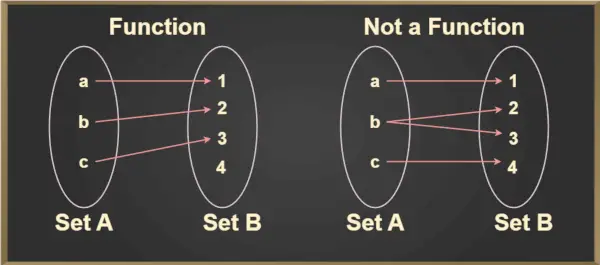
Test navpične črte

Test navpične črte se uporablja za ugotavljanje, ali je krivulja funkcija ali ne. Če katera koli krivulja prereže navpično črto v več kot eni točki, potem krivulja ni funkcija.

Predstavitev funkcij v matematiki

Funkcijo v matematiki predstavljamo kot,

y = f(x) = x + 3

Tu je množica vrednosti x domena funkcije, množica izhodnih vrednosti y pa sodomena funkcije. Tukaj je funkcija definirana za vsa realna števila, saj daje edinstveno vrednost za vsak x, vendar ni vedno mogoče dobiti izhoda za vsako vrednost x; v tem primeru definiramo funkcijo v dveh delih, to lahko razumemo kot

• f(x) = 1/(x – 2), kjer je x ≠ 2
• f(x) = x²kjer je x ∈ {R}

Funkcijo v matematiki lahko definiramo kot stroj, ki sprejme nekaj vnosa in daje edinstven rezultat. Funkcija f(x) = x²je spodaj opredeljen kot,

Funkcijo v matematiki lahko predstavimo z metodo treh kot,

• Niz urejenih parov
• Obrazec tabele
• Grafična oblika

Na primer, če predstavimo funkcijo kot f(x) = x³

Drug način za predstavitev iste funkcije je kot množica urejenih parov kot,

f = {(1,1), (2,8), (3,27)}

V zgoraj omenjenem nizu je domena funkcije D = {1, 2, 3}, območje funkcije pa R = {1, 8, 27}

Identifikacija funkcije

Funkcijo uvrščamo med posebne vrste relacije v matematiki. Obstajajo naslednja pravila, ki jih je mogoče uporabiti za identifikacijo funkcije:

• Relacija, v kateri je vsak vhod preslikan v edinstven izhod, je funkcija. To je imenovalo funkcijo ena proti ena.
• Relacija, v kateri sta dva vhoda (praslika), preslikana na en izhod, je prav tako funkcija. To je funkcija več proti eni.
• Relacija, v kateri je en vhod preslikan v dva različna izhoda, ni funkcija.
• Relacija, v kateri je veliko vhodov preslikanih v številne izhode brez posebnega pravila, ni funkcija.

Vrste funkcij

Drugačen Vrste funkcij se uporabljajo za reševanje različnih vrst matematičnih problemov, zlasti povezanih s krivuljami in enačbami. V matematiki obstajajo tri glavne vrste funkcij, ki temeljijo na preslikavi elementov iz množice A v množico B.

Injektivna funkcija ali funkcija ena proti ena

Funkcija, pri kateri ima vsak element domene ločeno sliko v kodomeni, se imenuje Injective oz Funkcija ena proti ena .

f: A → B pravimo, da je ena proti ena ali injektiven, če so slike različnih elementov A pod f različne, tj.

f(a ₁ ) = b ₁ , f(a ₂ ) = b ₂

kje₁, a₂∈ A in b₁, b₂∈ B

Surjektivne funkcije ali onto funkcija

Surjektivna funkcija je funkcija, pri kateri ima vsak element kodomene predsliko v domeni. Imenuje se tudi Na funkcijo kar pomeni, da je vsak element kodomene povezan z vsakim elementom domene. Noben element kodomene ne sme imeti prazne relacije. Število elementov kodomene in obsega je enako.

f: A → B pravimo, da je onto, če je vsak element B slika nekega elementa A pod f, tj. za vsak b ϵ B obstaja element 'a' v A, tako da je f(a) = b.

Bijektivna funkcija

Če ima funkcija lastnosti injektivne (ena proti ena) in surjektivne (na funkcijo), se funkcija imenuje Bijektivna funkcija . V bijektivni funkciji je vsak element domene povezan z vsakim elementom kodomene in obstaja tudi razmerje ena proti ena. To pomeni, da je število elementov kodomene in obsega enako in noben element v domeni ali kodomeni nima prazne relacije.

Na podlagi izhodnih vrednosti so funkcije razvrščene kot lihe in sode funkcije. Oglejmo si jih

Čudne funkcije

Liha funkcija je vrsta funkcije, ki kaže simetrijo glede na izvor. Natančneje, če je f(x) liha funkcija, kaže, da je f(-x) = -f(x)

Celotna funkcija

Soda funkcija je vrsta funkcije, ki kaže simetrijo glede na os y. Natančneje, če je f(x) soda funkcija, kaže, da je f(-x) = f(x)

lebdeči css

Kaj je funkcija v algebri?

Funkcija v algebra je enačba, za katero bo vsak x, ki ga je mogoče vključiti v enačbo, proizvedel natanko en rezultat, kot je y iz enačbe. Predstavljen je kot y = f(x), kjer je x neodvisna spremenljivka in y odvisna spremenljivka.

Na primer:

• y = 2x + 1
• y = 3x – 2
• y = 4y
• y = 5/x

Domena in obseg funkcije

Domena in obseg funkcije sta vhodna oziroma izhodna vrednost funkcije. Na primer, recimo, da imamo funkcijo, podano kot f(x) = x². Tukaj lahko vzamemo vsa realna števila kot vhodno vrednost x in izhod bo vedno pozitivno realno število. Zato je njegova domena množica vseh realnih števil, predstavljenih kot R, medtem ko je njeno območje množica pozitivnih realnih števil, predstavljenih kot R⁺

Sestava funkcij

Če sta f: A → B in g: B → C dve funkciji. Nato je sestava f in g označena kot f(g) in definirana kot funkcija megla = f(g(x)) za x ∈ A.

Vzemimo dve funkciji f(x) = x + 3 in g(x) = 2x²

megla = f(g(x))

⇒ megla = f(2x²)

⇒ zob = 2x²+ 3

Nauči se več, Sestava funkcije

Algebra funkcij

Algebra funkcij vključuje algebraične operacije, ki se izvajajo med dvema funkcijama. Spodaj je omenjena algebrska operacija za dve funkciji f(x) in g(x), definirani na realni vrednosti x:

• (f + g) (x) = f(x) + g(x)
• (f – g) (x) = f(x) – g(x)
• (f.g) (x) = f(x).g(x)
• (k f(x)) = k (f(x)); {Ker je k realno število}
• (f/g)(x) = f(x) /g(x); {Za g(x) ≠ 0}

Kaj je funkcija na grafu?

Funkcijo lahko enostavno predstavimo na grafu. Katera koli funkcija na grafu predstavlja krivuljo (vključno z ravno črto) v ravnini x-y, preslikano za njene vhodne in ustrezne izhodne vrednosti.

Če želite narisati funkcijo na a, najprej poiščite nekaj točk, ki ležijo na funkciji, nato pa te točke združite glede na geometrijsko mesto funkcije. Na primer, za prikaz funkcije (ravna črta) f(x) = y = 5x – 2 potrebujemo točko na grafu. Da bi našli točko, točko na grafu, najprej vzamemo naključne vrednosti x in nato poiščemo njihove ustrezne vrednosti y, kot je

f(x) = y = 5x- 2

če je x = 0, y = 5(0) – 2 = -2 ⇒ (x, y) = (0, -2)

če je x = 1, y = 5(1) – 2 = 3 ⇒ (x, y) = (1, 3)

če je x = 2, y = 5(2) – 2 = 8 ⇒ (x, y) = (2, 8)

java string replaceall

Zdaj, ko te točke združimo, lahko dobimo graf funkcije y = 5x – 2

Grafične funkcije

Poznavanje vrednosti x omogoča, da je funkcija f(x) predstavljena na grafu. Ker je y = f(x), lahko najdemo povezano vrednost za y tako, da začnemo z vrednostmi x. Posledično lahko narišemo graf v koordinatni ravnini z uporabo vrednosti x in y. Razmislite o naslednjem scenariju:

Predpostavimo, da je y = x + 3

Ko je x = 0, je y = 3

Podobno,

• x = -2, y = -2 + 3 = 1
• x = -1, y = -1 + 3 = 2
• x = 1, y = 1 + 3 = 4
• x = 2, y = 2 + 3 = 5
• x = 3, y = 3 + 3 = 6

Posledično lahko narišemo graf za funkcijo x + 3 z uporabo teh vrednosti.

Skupne funkcije

Nekatere skupne funkcije, ki se običajno uporabljajo v matematiki, so obravnavane spodaj:

Prava funkcija

Prava funkcija v matematiki se nanaša na funkcijo, katere domena in obseg sta podmnožici realnih števil (označenih z ℝ). Preprosteje rečeno, realna funkcija je matematično pravilo ali razmerje, ki vsakemu vnosu realnega števila dodeli vrednost realnega števila.

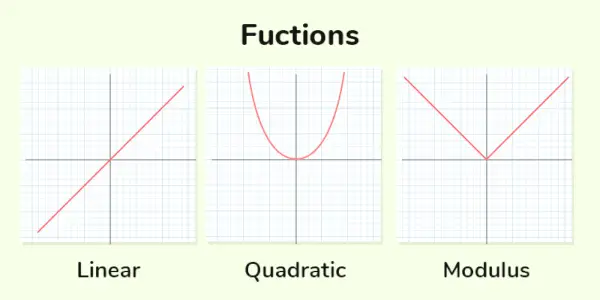
Realne funkcije

Polinomska funkcija

Funkcija, v kateri so eksponenti algebraičnih spremenljivk nenegativna cela števila, se imenuje Polinomska funkcija . Če je potenca spremenljivke 1, se imenuje linearna funkcija, če je potenca 2, se imenuje kvadratna funkcija, če je potenca 3, pa se imenuje kubična funkcija. Nekaj ​​primerov polinomskih funkcij je navedenih spodaj:

• y = x²
• y = 2x + 3
• y = 3x³

Polinomsko funkcijo lahko nadalje razvrstimo v naslednje vrste:

Linearna funkcija : Linearne funkcije so tiste, pri katerih je največja moč spremenljivke 1. Splošna oblika Linearna funkcija je y = mx + c

Kvadratna funkcija : Kvadratna funkcija je tista, pri kateri je največja moč spremenljivke 2. Splošna oblika kvadratna funkcija je, sekira ² + bx + c = 0

Kubična funkcija : Kubična funkcija so tiste, pri katerih je največja moč spremenljivke 3. Splošna oblika kubične funkcije je podana kot sekira ³ + bx ² + cx + d = 0

Inverzna funkcija

Inverzna funkcija je funkcija, ki vsebuje obratno funkcijo druge funkcije. Recimo, da imamo funkcijo y = f(x), potem bo njena obratna funkcija x = f^-1(y). Pri y = f(x) je domena x in obseg y, medtem ko je v primeru x = f^-1(y), domena je y in obseg je x. Tako lahko rečemo, da je domena izvirne funkcije območje njene inverzne funkcije, območje izvirne funkcije pa območje izvirne funkcije. Nekaj ​​primerov inverznih funkcij je,

• y = torej^-1(x)
• y = x^-1

Območna funkcija

Območna funkcija se običajno nanaša na matematično funkcijo, ki izračuna površino geometrijske oblike ali območja. Funkcija območja sprejme enega ali več parametrov kot vhod in vrne območje ustrezne oblike. Spodaj so obravnavane nekatere funkcije območja:

Območje delovanja kroga : Območje kroga (A) je funkcija njegovega polmera (r), tako da

A = πr ²

Območje funkcije trikotnika : Območje trikotnika (A) je funkcija svoje osnove (b) in višine (h), tako da

A = (bh)/2

Eksponentna funkcija

Eksponentna funkcija je tista, ki je predstavljena kot f(x) = e^x. Pogosto se uporablja za prikaz hitre rasti ali propadanja.

Logaritemska funkcija

Logaritemska funkcija je matematična funkcija, ki predstavlja inverzno operacijo potenciranja. Predstavljen je kot f(x) = log x.

Stropna funkcija

Stropna funkcija , označeno kot ⌈x⌉, zaokroži realno število x navzgor na najbližje celo število, ki je večje ali enako x. Z drugimi besedami, najde najmanjšo celoštevilsko vrednost, ki je večja ali enaka x.

Talna funkcija

Funkcija Floor, označena kot ⌊x⌋, zaokroži realno število x navzdol na najbližje celo število, ki je manjše ali enako x. Z drugimi besedami, najde največjo celoštevilsko vrednost, ki je manjša ali enaka x.

Funkcija modula

Modulna funkcija , znana tudi kot funkcija absolutne vrednosti, vrne velikost ali velikost realnega števila ne glede na njegov predznak. Funkcija modula je označena kot ∣x∣, kjer je x vhodna vrednost.

Funkcija Signum

Signum funkcija , znana tudi kot funkcija znaka ali funkcija signum, je matematična funkcija, ki vrne predznak realnega števila. Označuje, ali je število pozitivno, negativno ali nič.

Trigonometrične funkcije

Trigonometrične funkcije so matematične funkcije, ki povezujejo kote pravokotnega trikotnika z dolžinami njegovih stranic. Šest primarnih trigonometričnih funkcij je sinus (sin), kosinus (cos), tangens (tan), kosekans (cosec), sekans (sek) in kotangens (cot).

Kompleksne funkcije

Vsaka funkcija, pri kateri je vhodna spremenljivka kompleksna funkcija, se imenuje kompleksna funkcija. Kompleksno število je število, ki ga lahko narišemo na kompleksno ravnino. V kompleksno število imamo realno in imaginarno število. Kompleksno število (z) je predstavljeno kot z= x + iy in kompleksna funkcija je predstavljena kot f(z) = P(x, y) + iQ(x, y)

Uporaba funkcij

Ko rečemo, da je spremenljiva količina y funkcija spremenljive količine x, pomenimo, da je y odvisna od x in da je vrednost y določena z vrednostjo x. To odvisnost lahko izrazimo na naslednji način: f = y (x).

ekta kapoor igralec

• Polmer kroga lahko uporabimo za izračun površine kroga. Polmer r vpliva na območje A. Izjavljamo, da je A funkcija r v matematičnem jeziku funkcij. Zapišemo lahko A = f(r) =π×r²
• Prostornina krogle V je funkcija njenega polmera. V = f(r) = 4/3×r³označuje odvisnost V od r.
• Sila je funkcija pospeška telesa s fiksno maso m. F = g(a) = m×a.

Ljudje preberejo tudi:

• Razmerje in funkcija
  
• Domena in območje trigonometričnih funkcij
• Območje funkcije
• Hiperbolična funkcija

Primeri o funkciji

Primer 1: Za dve funkciji sta f in g definirani kot f(x) = x ² in g(x) = ln(2x). Poiščite sestavljeno funkcijo (gof)( x)

rešitev:

podano:

• f(x) = x²
• g(x) = ln(2x)

(gof )( x ) = g (f (x))

[g (f (x)] = ln (2f (x))

= ln(2x²)

= 2 ln(√2x)

Tako je (gof)(x) = 2 ln(√2x)

Primer 2: Poiščite rezultat funkcije g(t)= 6t ² + 5 at

• (i) t = 0
• (ii) t = 2

rešitev:

Dana funkcija,

g(t)= 6t²+ 5t

• (i) t = 0

g(0) = 6(0)²+5(0) = 0 + 0

g(0) = 0

• (ii) t = 2

g(2) = 6(2)²+5 (2)

g(2) = 24 + 10

g(2) = 34

velikost besedila iz lateksa

Primer 3: Dolžina pravokotnika je petkrat večja od njegove širine, izrazite površino pravokotnika kot funkcijo njegove dolžine.

rešitev:

Naj bo dolžina pravokotnika l in širina pravokotnika b

zdaj,

• b = l/5

Ploščina pravokotnika (A) = l × l/5 = l²/5

Torej je ploščina pravokotnika kot funkcija njegove dolžine,

A(l) = l ² /5

Vadite naloge o tem, kaj je funkcija

1. Dana je funkcija f(x)=3x+5

• Poišči f(2)
• Poiščite f(−1)
• Določite domeno in obseg funkcije.

2. Dana je funkcija g(x)=x ² – 4x + 3

• Poiščite korene funkcije.
• Poiščite g(3) in g(0).
• Določite oglišče funkcije.

3. Podani sta dve funkciji f(x)=x + 2 in h(x)=2x – 3

• Poiščite sestavljeno funkcijo (f ∘ h) (x)
• Oceni (f ∘ h)(2)

Povzetek – Kaj je funkcija

Funkcija v matematiki je posebna relacija med vhodnimi vrednostmi (domena) in izhodnimi vrednostmi (obseg), kjer je vsak vhod povezan z edinstvenim izhodom. Funkcije, predstavljene kot y = f(x), imajo posebne značilnosti in jih je mogoče vizualizirati z uporabo urejenih parov, tabel ali grafov. Bistveni so pri različnih matematičnih problemih in so različnih vrst, vključno z injektivnimi (ena proti ena), surjektivnimi (onto) in bijektivnimi (oboje). Funkcije je mogoče preizkusiti s testom navpične črte in so nadalje razvrščene v polinomske, inverzne, eksponentne, logaritemske in trigonometrične funkcije. Razumevanje funkcij vključuje prepoznavanje njihove domene, obsega in pravil, ki jih definirajo. Primeri vključujejo preproste linearne funkcije, kot je y = 2x + 1 in kompleksne sestave funkcij. Funkcije igrajo ključno vlogo v algebri, geometriji in računu, saj pomagajo pri predstavitvi in ​​analizi matematičnih odnosov in pojavov v realnem svetu.

Pogosta vprašanja o tem, kaj je funkcija

Kaj je definicija funkcije?

Odnos f, definiran na množici A do druge množice B, se v matematiki imenuje funkcija, če ima vsaka vrednost A edinstveno vrednost v množici B.

Kako napisati funkcijo v matematiki?

Funkcija f je v matematiki predstavljena kot f: A → B in je definirana kot, f(x) = x + 2. Tu imamo za vsako edinstveno vrednost x edinstveno vrednost y.

Kako preoblikovati funkcijo?

Funkcijo lahko preprosto pretvorimo v druge funkcije tako, da preprosto izvedemo osnovne algebraične operacije na funkciji. Različne transformacije funkcije so refleksija, translacija, rotacija itd.

Kaj je racionalna funkcija?

Funkcija ulomka, kjer sta števec in imenovalec polinomski funkciji, se imenuje racionalna funkcija. Nekaj ​​primerov racionalne funkcije je,

• f(x) = x ² /(2x + 3)
• g(x) = (6x + 3)/(x – 1), itd.

Kaj je linearna funkcija?

Algebraična funkcija, pri kateri je vsak člen funkcije konstanten ali ima potenco ena, se imenuje linearna funkcija. Nekateri primeri linearne funkcije so:

• f(x) = 2x + 3
• g(x) = x – 5 itd.

Kaj sta domena in kodomena funkcije?

Če definiramo funkcijo kot, y = f(x). Potem so domena x vse vrednosti x, za katere je rezultat y edinstvena vrednost. In sodomena y je množica vseh vrednosti y za vsako vrednost x.

Kako prepoznate funkcijo v matematiki?

Če ima katera koli vhodna vrednost (x) domene v relaciji več kot eno sliko (y), potem ta relacija nikoli ne more biti funkcija. Torej, če se vrednost x ponovi v urejenem paru, potem to nikoli ni funkcija.