Simboli množice so skupni izraz, ki se uporablja za vse simbole, ki se uporabljajo v teoriji množic, ki je veja matematike, ki se ukvarja z zbiranjem predmetov in njihovih različnih lastnosti. Niz je dobro definirana zbirka predmetov, kjer se vsak predmet v zbirki imenuje element in vsak element niza sledi zelo specifičnemu pravilu. Na splošno se velike črke angleških abeced uporabljajo za označevanje množic, nekatere črke pa označujejo nekatere posebne množice v teoriji množic.
Pri preučevanju te veje matematike se uporablja veliko simbolov, nekateri pogosti simboli so {}, |, :, ∈, ∉, ⊆, U, Ø itd. O vseh teh simbolih bomo podrobno razpravljali v članku vključno z zgodovino teh simbolov. Začnimo torej našo pot učenja o različnih simbolih množic, ki se uporabljajo v teoriji množic.
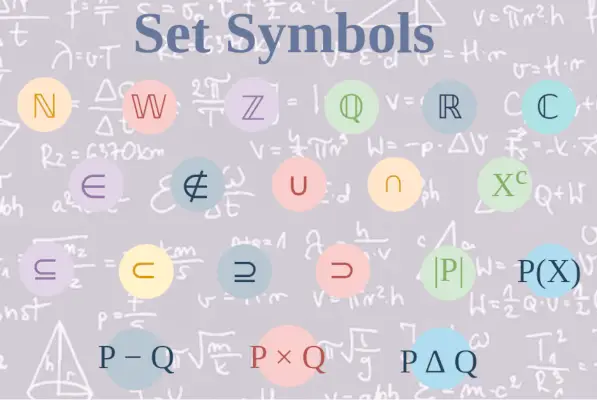
Kazalo
- Kaj so nastavljeni simboli?
- Zgodovina nabora simbolov
- Osnovni koncepti množice simbolov
- Nastavite simbole pri matematiki
- Simboli teorije množic
- Rešeni primeri nastavljenih simbolov
- Vadite vprašanje za nabor simbolov
- pogosta vprašanja
Kaj so nastavljeni simboli?
Simboli nabora so osnovni gradniki matematike, ki se uporabljajo za predstavitev in opis skupin predmetov, števil ali predmetov, ki imajo podobne lastnosti. Ti simboli ponujajo jasen in dosleden pristop k sporočanju težkih idej o nizih in njihovih interakcijah. Najbolj značilen simbol za množico je ∈, ki pomeni članstvo in se izgovarja kot pripada. ∈ označuje, da je element del določene množice.
Nasprotno pa ∉ pomeni, da element ni del niza. ⊆, ⊂, ∪, ∩, ∅ itd. so nekateri pogosti primeri simbolov v teoriji množic. Ti in drugi simboli omogočajo matematikom, da definirajo operacije, specificirajo operacije in oblikujejo natančne matematične trditve, s čimer postavljajo temelje za različne matematične posebnosti in praktične uporabe.
Preberite več o Teorija množic .
Primer nabora simbolov
Za ponazoritev uporabimo simbol, ki označuje presečišče množic. Naj sta E in F dve množici, tako da je množica E = {1, 3, 5, 7} in množica F = {3, 6, 9}. Potem simbol ∩ predstavlja presečišče med obema nizoma, tj. E ∩ F.
Tukaj E ∩ F vsebuje vse elemente, ki so skupni v obeh množicah E in F, tj. {3}.
Skratka, simbol ∩ se uporablja za identifikacijo elementov, ki si jih delita dva ali več nizov. Presek proizvede samo nize, ki imajo elemente, ki si jih delijo vsi nizi, ki se sekajo.
Izvedite več o Presečišče množic .
Zgodovina nabora simbolov
Med letoma 1874 in 1897 je poklical nemški matematik Georg Ferdinand Ludwig Philipp Cantor razvil abstraktno teorijo, imenovano Teorija množic. Predlagal ga je med raziskovanjem nekaterih dejanskih vprašanj, ki vključujejo posebne oblike neskončnih nizov realnih števil. Množica je po pojmovanju skupina določenih določenih in ločenih predmetov opazovanja. Vse te stvari se imenujejo člani ali komponente nabora. Lastnost realnih algebraičnih številskih kombinacij je temelj Cantorjeve teorije.
Osnovni koncepti množice simbolov
Na različnih stopnjah šolanja teorije množic so zajete različne ideje. Predstavitev niza, tipi niza, operacije niza (kot sta unija in presek), kardinalnost niza in relacije itd. so med bistvenimi pojmi. Nekateri bistveni pojmi v teoriji množic so naslednji:
Univerzalni set
Velika črka 'U' se običajno uporablja za predstavitev univerzalnega niza. Občasno ga simbolizira tudi ε(epsilon). Je množica, ki vsebuje vse elemente drugih množic in tudi svojo lastno.
Dopolnitev kompleta
Komplement množice obsega vse sestavine univerzalne množice, razen elementov množice, ki jo obravnavamo. Če je A množica, bodo njeni komplementi vsebovali vse člane navedene univerzalne množice (U), ki niso vključeni v A. Komplement niza je označen ali izražen kot A' ali Acin je definiran kot:
A’= {x ∈ U: x ≠ A}
Preberite več o Dopolnitev kompleta .
Set Builder Notation
Notacija Set Builder je metoda za predstavitev množic na tak način, da kjer nam ni treba navesti vseh elementov množice, moramo samo določiti pravilo, ki mu sledijo vsi elementi množice. Nekaj primerov teh zapisov je:
Če je A zbirka realnih števil.
A = {x : x ∈ R}
Če je A zbirka naravnih števil.
A = {x : x> 0 in x ∈ Z]
Kje Z je niz celih števil.
Preberi več, Predstavitev množic .
Nastavite simbole pri matematiki
Za sklicevanje na različne stvari in zneske simbol nabora pogosto uporablja vnaprej določen seznam spremenljivih simbolov. Če želite prebrati in ustvariti zapis niza, morate najprej razumeti, kako uporabljati simbole v različnih situacijah. Oglejmo si vse zapise in simbole teorije množic, ki se nanašajo na operacije, relacije in tako naprej, skupaj z njihovimi pomeni in primeri v tej kategoriji.
Simboli, ki se uporabljajo v številskem sistemu
Simboli, ki se uporabljajo v številskih sistemih, so vključeni v spodnjo tabelo:
| Simbol | Ime | Pomen/definicija | Primer |
|---|---|---|---|
| W ali 𝕎 | Cela števila | To so naravna števila. | Vemo, da je N = {1, 2, 3, . . . } 1 ∈ N |
| N ali ℕ | Naravna števila | Naravna števila se včasih imenujejo števila za štetje, ki se začnejo z 1. | Vemo, da je W = {1, 2, 3, 4, 5, . . . } 0 ∈ W |
| Z ali ℤ | Cela števila | Cela števila so primerljiva s celimi števili, le da vsebujejo tudi negativne vrednosti. | Vemo, da je Z = {. . . , -3, -2, -1, 0, 1, 2, 3 . . .} -6 ∈ Z |
| Q ali ℚ | Racionalna števila | Racionalna števila so tista, ki so navedena kot a/b. V tem primeru sta a in b celi števili z b ≠ 0. | Q= x=a/b, a, b ∈ Z in b ≠ 0 2/6 ∈ Q |
| P ali ℙ | Iracionalna števila | Tista števila, ki jih ni mogoče predstaviti v obliki a/b, se imenujejo iracionalna števila, tj. vsa realna števila, ki niso racionalna. gimp shrani kot jpeg | P = x π in ∈ P |
| R ali ℝ | Realna števila | Cela števila, racionalna števila in iracionalna števila sestavljajo realna števila. | R = x 6,343434 ∈ R |
| C ali ℂ | Kompleksna števila | Kompleksno število je kombinacija realnega in imaginarnega števila. | C= z = a + bi, a, b ∈ R 6 + 2 jaz ∈ C |
Simboli teorije množic
Ločila so posebni znaki ali zaporedja znakov, ki označujejo začetek ali konec določenega stavka ali telesa funkcije določenega niza. Sledijo simboli in pomeni teorije množic ločil:
| Simbol | Ime | Pomen/definicija | Primer |
|---|---|---|---|
| {} | Set | Znotraj teh oklepajev je kup elementov/številk/črk v nizu. | {15, 22, c, d} |
| | | Tako, da | Ti se uporabljajo za sestavo nabora z določitvijo, kaj je v njem. | q> 6 Stavek podaja zbirko vseh q-jev, tako da je q večji od 6. |
| : | Tako, da | Simbol : se včasih uporablja namesto | simbol. | Zgornji stavek lahko zapišemo tudi kot q. |
Množice in relacijski simboli v teoriji množic
Simboli teorije množic se uporabljajo za identifikacijo določene množice, pa tudi za določanje/prikaz odnosa med različnimi množicami ali odnosi znotraj množice, kot je razmerje med množico in njeno sestavino. Spodnja tabela prikazuje takšne simbole odnosov, skupaj z njihovimi pomeni in primeri:
| Simbol | Ime | Pomen/definicija | Primer |
|---|---|---|---|
| a ∈ A | Je sestavni del | To določa, da je element član določenega niza. | Če je množica A={12, 17, 18, 27}, lahko rečemo, da je 27 ∈ a. |
| b ∉ B | Ni sestavni del | To pomeni, da element ne pripada določenemu nizu. | Če je množica B={c, d, g, h, 32, 54, 59}, noben element razen tistega v množici ne pripada tej množici. Na primer, 18 ∉ B. |
| A = B | Razmerje enakosti | Predloženi kompleti so enakovredni v smislu, da imajo enake komponente. | Če postavite P={16, 22, a} in Q={16, 22, a}, potem je P=Q. |
| A ⊆ B | Podnabor | Ko so vsi elementi A prisotni v B, je A podmnožica B. | A= {31, b} in B={a, b, 31, 54} {31, b} ⊆ {a, b, 31, 54} |
| A ⊂ B | Pravilna podmnožica | Pravimo, da je P prava podmnožica B, če je podmnožica B in ni enaka B. | A= {24, c} in B={a, c, 24, 50} A ⊂ B |
| A ⊄ B | Ni podnabor | Posledično množica A ni podmnožica množice B. | A = {67,52} in B = {42,34,12} A ⊄ B |
| A ⊇ B | Superset | A je nadmnožica B, če je množica B podmnožica A. Množica A je lahko enaka ali večja od množice B. | A = {14, 18, 26} in B = {14, 18, 26} {14, 18, 26} ⊇{14, 18, 26} |
| A ⊃ B | Pravilen superset | Množica A ima več elementov kot množica B, saj je nadmnožica B. | {14, 18, 26, 42} ⊃ {18,26} |
| A ⊅ B | Ni Superset | Če vsi elementi B niso prisotni v A, A ni prava nadmnožica B. | A = {11, 12, 16} in B = {11, 19} {11, 12, 16} ⊅ {11, 19} |
| Ø | Prazen komplet | Prazen ali ničelni niz je tisti, ki ne vključuje nobenih elementov. | {22, y} ∩ {33, a} = Ø |
| IN | Univerzalni set | Množica, ki vsebuje elemente iz vseh ustreznih množic, vključno z lastno. | Če je A = {a,b,c} in B = {1,2,3,b,c}, potem je U = {1,2,3,a,b,c} |
| |A| ali n{A} | Kardinalnost niza | Kardinalnost se nanaša na število predmetov v določeni zbirki. | Če je A= {17, 31, 45, 59, 62}, potem je |A|=5. |
| P(X) | Power Set | Nabor moči je niz vseh podmnožic množice X, vključno s samo množico in ničelno množico. | Če je X = {12, 16, 19} P(X) = {12, 16, 19}={{}, {12}, {16}, {19}, {12, 16}, {16, 19}, {12, 19}, {12, 16, 19}} |
Simboli na osnovi operatorjev v teoriji množic
Na primerih bomo proučevali simbole teorije množic in pomene za številne operacije, kot so unija, komplement, presek, razlika in druge.
| Simbol | Ime | Pomen/definicija | Primer |
|---|---|---|---|
| A ∪ B | Zveza nizov | Združitev nizov ustvari popolnoma nov niz z združevanjem vseh komponent v danih nizih. | A = {p, q, u, v, w} B = {r, s, x, y} A ∪ B (A unija B) = {p, q, u, v, w, r, s, x, y} |
| A ∩ B | Presečišče množic | Skupna komponenta obeh množic je vključena v presečišče. | A = {4, 8, a, b} in B = {3, 8, c, b}, potem A ∩ B = {8, b} |
| XcALIX' | Dopolnitev kompleta | Dopolnilo kompleta sestavljajo vse stvari, ki ne sodijo v dani komplet. | Če je A univerzalna množica in je A = {3, 6, 8, 13, 15, 17, 18, 19, 22, 24} in B = {13, 15, 17, 18, 19}, potem je X′ = A – B ⇒ X′ = {3, 6, 8, 22, 24} |
| A − B | Nastavi razliko | Različni niz je niz, ki vsebuje elemente iz enega niza, ki jih ni v drugem. | A = {12, 13, 15, 19} in B = {13, 14, 15, 16, 17} A – B = {12, 19} |
| A × B | Kartezični produkt množic | Kartezični produkt je produkt urejenih komponent množic. | A = {4, 5, 6} in B = {r} Zdaj je A × B = {(4, r), (2, r), (6, r)} 'kaj je 10 od 100' |
| A ∆ B | Simetrična razlika množic | A Δ B = (A – B) U (B – A) označuje simetrično razliko. | A = {13, 19, 25, 28, 37}, B = {13, 25, 55, 31} A ∆ B = { 19, 28, 37, 55, 31} |
Preberi več
- Vrste kompletov
- Delovanje na nizih
Rešeni primeri nastavljenih simbolov
1. primer: dana sta dva niza s P={21, 32, 43, 54, 65, 75} in Q={21, 43, 65, 75, 87, 98}, kakšna je vrednost P∪Q?
odgovor:
P={21, 32, 43, 54, 65, 75} in Q={21, 43, 65, 75, 87, 98}
P∪Q={21, 32, 43, 54, 65, 75, 87, 98}
Primer 2: Kakšna je vrednost |Y| če je Y={13, 19, 25, 31, 42, 65}?
odgovor:
|Y| = Kardinalnost množice=število elementov v množici je rešitev.
|Y| = n(Y)=6, saj ima množica Y 6 elementov.
Primer 3: Podani sta dve množici z vrednostmi P={a,c,e} in Q={4,3}, določi njun kartezični produkt.
odgovor:
Kartezični produkt = P × Q
Če je P={b, d, f} in Q={5, 6}
Potem je P × Q={(b,5), (d,6), (b,5), (d,6), (b,5), (d,6), (b,5), (d ,6), (b,5), (d,6)}
Primer 4: Predpostavimo, da je P = {x: x naravno celo število in večkratnik 24, Q = {x: x je naravno število, manjše od 8}. Določite P ∪ Q.
odgovor:
Glede na to
P = {1, 2, 3, 4, 6, 8, 12, 24}
ZDA koliko mestQ = {1, 2, 3, 4, 5, 6, 7}
Posledično je P ∪ Q = {1, 2, 3, 4, 5, 6, 7, 8, 12, 24}
Primer 5: Predpostavimo, da je P = {3, 5, 7}, Q = {2, 3, 4, 6}. Poišči (P ∩ Q)'.
odgovor:
Podano, P = {4, 6, 8}, Q = {3, 4, 5, 7}
P ∩ Q = {4}
zato
(P ∩ Q)' = {3, 5, 6, 7, 8}
Primer 6: Če je P = {4, 5, 7, 8, 9, 10} in Q = {3, 5, 7, 9, 12, 14}, določite
(i) P-Q in (ii) P-Q.
odgovor:
podano,
P = {4, 5, 7, 8, 9, 10} in Q = {3, 5, 7, 9, 12, 14}
(i) P – Q = {4, 8, 10}
(ii) Q – P = {3, 12, 14}
Vprašanja za vajo za niz simbolov
Vprašanje 1: Glede na sklope:
- A = {2, 4, 6, 8}
- B = {4, 8, 12, 16}
Določite elemente v uniji množic A in B.
2. vprašanje: Razmislimo o sklopih:
- X = {1, 2, 3, 4, 5}
- Y = {3, 4, 5, 6, 7}
Poiščite presečišče množic X in Y.
3. vprašanje: Recimo, da imate nize:
- P = {a, b, c, d}
- Q = {c, d, e, f}
Izračunajte elemente v množici P – Q kot tudi Q – P.
4. vprašanje: Recimo, da imate komplete:
- U = {1, 2, 3, 4, 5}
- V = {4, 5, 6, 7}
Ugotovite, ali je množica V podmnožica množice U.
5. vprašanje: Razmislite o sklopih:
- S = {jabolko, banana, pomaranča, hruška}
- T = {hruška, mango, češnja}
Poiščite kartezični produkt množic S in T.
6. vprašanje: Recimo, da imate univerzalni niz:
- U = {a, b, c, d, e, f, g, h, i, j}
In kompleti:
- E = {b, d, f, h, j}
- F = {a, c, e, g, i}
Izračunaj komplement množic E in F glede na univerzalno množico U.
Pogosta vprašanja o naboru simbolov
1. Določite Set Symbol.
Simbol množice je veja, ki preučuje skupine entitet/števil/predmetov, njihove odnose z drugimi množicami, različne operacije (unija, presečišče, komplement in razlika) in povezane značilnosti.
2. Kaj predstavlja ta simbol ⊆?
Simbol ⊆ pomeni, da je podmnožica. Podnabor je nabor, katerega elementi so bili dodani, kot da bi bili vsi elementi drugega nabora.
3. Kaj pomeni ∪ v nizih?
‘∪’ je znak za unijo množice. A ∪ B je množica, ki vsebuje vse elemente množic A in B.
4. Kaj predstavlja P = Q?
Če je množica P enaka množici Q, potem sta člana P in Q enaka. Na primer:
P = {4,5,6} in Q = {6,5,4}
Posledično je P = Q.
5. Kaj v matematiki pomeni ∩?
'∩' pomeni združitev dveh množic. A ∩ B je niz, ki vsebuje elemente, ki si jih delita A in B.
6. Kaj je ∈ v množicah?
∈ je znak, ki pomeni 'pripada'. Če je b ∈ B, to pomeni, da je b element B.
7. Kakšna je množica N = {1, 2, 3, 4, 5, . . .} poznan kot?
Množica naravnih števil je definirana kot N = {1, 2, 3, 4, 5, …} Vsebuje vsa pozitivna števila, ki segajo od 1 do neskončnega števila. Ta zbirka je ključnega pomena za matematiko in zagotavlja okvir za razvrščanje in štetje.
8. Kaj je A × B v množicah?
Kartezični produkt množic A in B je prikazan kot A x B v simbolu množice. To je množica, ki vključuje vse možne urejene pare, v katerih je prvi element črpan iz množice A, drugi pa iz množice B.
9. Kako boste prebrali A ∩ B?
A∩B se izgovori A presečišče B. Označuje množico, ki vsebuje elemente, ki so skupni v obeh množicah.
10. Kaj pomeni Ø v teoriji množic?
V teoriji množic je ideja prazne množice, ki nima elementov, označena s simbolom Ø (izgovorjena prazna množica).
11. Kaj je AUB?
AUB v matematiki pomeni unijo množic A in B. Nanaša se na množico, ki vključuje vse elemente iz obeh množic A in B.
12. Je ∅ enak {}?
Da, ∅ in {} oba predstavljata prazno množico v matematiki. Tako sta oba različna zapisa iste stvari.
