logo

TechCodeview

Formula za obrestne obresti

Sestavljene obresti so obresti, ki se izračunajo glede na znesek posojila ali depozita, pri čemer se obresti izračunajo za glavnico in prejšnje zaslužene obresti.

Skupna razlika med sestavljenimi in preprostimi obrestmi je, da v obrestno obrestovanje , se obresti obračunavajo tako za glavnico kot tudi za predhodno zaslužene obresti, medtem ko so navadne obresti odvisne le od vložene glavnice.



Kazalo

Kaj so obrestne obresti?

Sestavljene obresti so obresti na glavnico in obresti na glavnico. Beseda Compound Interest je sestavljena iz dveh besed Sestavljeno, kar pomeni sestavljeno iz dveh ali več, in obresti pomeni denar, zaslužen s posojanjem zneska. Zato so obrestne obresti denar, zaslužen s posojanjem, in so sestavljene iz dveh vrst obresti, ki sta:

  • Obresti na znesek glavnice
  • Obresti na obresti, zaslužene na znesek glavnice v obdobju

Opredelitev obrestnih obresti

Obrestno obrestovanje so obresti, obračunane na glavnico in prej pridobljene obresti. Označena je s C.I. Zelo uporaben je za naložbe in namene odplačevanja posojil. Znan je tudi kot obresti na obresti.



oblikovalski vzorec gradbenika

Obrestno obrestovanje je zelo uporaben v bančnem in finančnem sektorju ter uporaben tudi v drugih sektorjih. Nekatere njegove uporabe so:

  • Rast prebivalstva države
  • Vrednost naložbe v določenem časovnem obdobju.
  • Za iskanje napihnjenih stroškov in amortizirane vrednosti katerega koli artikla.
  • Za napovedovanje rasti katere koli institucije ali države.

Sestavljene obresti (C.I) = znesek – glavnica

Formula za obrestne obresti

Obrestno obrestovanje se izračuna po izračunu skupnega zneska v določenem časovnem obdobju na podlagi obrestne mere in začetne glavnice. Za začetno glavnico P, letno obrestno mero r, časovno obdobje t v letih, pogostost, kolikokrat se obresti obračunajo letno n, je formula za izračun CI naslednja:



CI = P(1 + r/100) n – str

Zgornja formula za izračun obrestne mere je dodana v spodnji slikovni obliki:

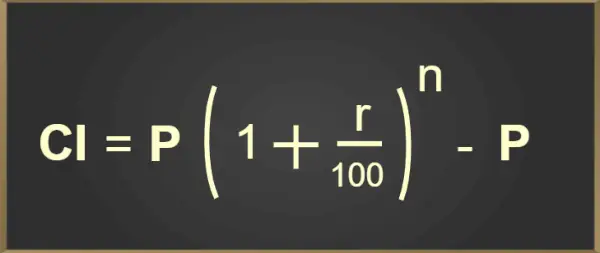
Formula za obrestne obresti

Formula za obrestne obresti

Kje,

  • P = glavni
  • r = obrestna mera
  • n = število obresti na leto
  • t = Čas (v letih)

Formulo za obresti lahko zapišemo kot:

Sestavljene obresti = A – P

Kje,

  • A = Skupni znesek denarja po sestavitvi
  • P = začetni znesek glavnice

    Sestavljene obresti = P(1 + r/n) nt -P

    Kje,

    • P = začetni znesek glavnice
    • r = letna obrestna mera
    • n = Število sestavljenih obresti
    • t = število let

    Obrestne obresti se lahko izračunajo letno, polletno, četrtletno, mesečno, dnevno itd., v skladu z zahtevami.

    Kako izračunati obrestne obresti?

    Obrestno obrestovanje so plačane obresti na glavnico in nabrane obresti. Obresti, zaslužene v vsakem intervalu, se prištejejo začetni glavnici, tako da se glavnica povečuje.

    Za iskanje obrestnih obresti uporabite naslednje metode.

    Korak 1: Navedena je opomba, glavnica, stopnja in časovno obdobje

    2. korak: Izračunajte količino z uporabo formule A = P(1 + r/100) n

    3. korak: Poiščite obrestne obresti po formuli CI = znesek – glavnica

    V rednih časovnih presledkih se do tedaj nabrane obresti povežejo z obstoječim zneskom glavnice, nato pa se obračunajo obresti izračunana za novega ravnatelja . Nova glavnica je enaka vsoti začetne glavnice in do tedaj nabranih obresti.

    Sestavljene obresti = obresti na glavnico + obresti na obresti glavnice (od drugega leta naprej)

    Sestavljene obresti se izračunavajo v rednih intervalih, kot so letno (letno), polletno, četrtletno, mesečno, itd.; Podobno je, če ponovna naložba obrestnega dohodka iz naložbe povzroči, da denar sčasoma raste hitreje! To je točno tisto, kar obrestne mere naredijo denarju. Banke ali katera koli finančna organizacija izračuna znesek samo na podlagi obresti.

    Formula za obrestne obresti – izpeljava

    Formula obrestne obresti je močno orodje, ki se uporablja v financah za izračun zasluženih ali plačanih obresti na začetni znesek glavnice, ki vključuje začetno glavnico in obresti, nabrane v prejšnjih obdobjih. Formula za obrestne obresti je podana z:

    A = P levo(1 + frac{r}{n}desno)^{nt}

    Kje,

    • A je prihodnja vrednost naložbe ali posojila, vključno z obrestmi
    • P je znesek glavnice (začetna naložba ali znesek posojila)
    • r je letna obrestna mera (kot decimalka)
    • n je število zaračunanih obresti na leto
    • t je čas, za katerega je denar vložen ali izposojen, v letih

    Enostavna formula obresti

    Enostavne obresti se obračunajo le na glavnico. Lahko ga predstavimo s formulo ,

    A = P + P cdot r cdot t

    Formula obrestne obresti z neprekinjenim obrestom

    Če se obresti obračunavajo neprekinjeno (neskončno velikokrat na leto), se formula za obrestne obresti izpelje z uporabo formule za neprekinjeno obračunavanje:

    A = P cdot e^{rt}

    Kje,

    • e je Eulerjevo število (približno 2,71828)
    • P je znesek glavnice
    • r je letna obrestna mera
    • t je čas v letih

    Splošna formula za obrestne obresti

    Za izpeljavo splošne formule za obrestne obresti upoštevajmo obrestne obresti n-krat na leto.

    če P se izračuna n-krat na leto z letno obrestno mero r, obresti r se delijo z n in uporabijo n-krat na leto. Tako po t letih formula postane:

    A = P levo(1 + frac{r}{n}desno)^{nt}

    Kje,

    • frac{r}{n} predstavlja obrestno mero na obdobje obračunavanja.
    • nt je skupno število obdobij sestavljanja v t letih.

    to formula ponazarja, kako začetni znesek glavnice raste skozi čas, ko se obresti obračunavajo v rednih intervalih . Ko se n približuje neskončnosti (tj. neprekinjeno združevanje), formula konvergira proti formuli zveznega združevanja A = P cdot e^{rt}.

    V povzetku, formula obrestne obresti A = P levo(1 + frac{r}{n}desno)^{nt} je rezultat formule neprekinjenega mešanja, prilagojene za diskretna obdobja mešanja na leto. Omogoča izračun prihodnje vrednosti naložbe ali posojila, pri čemer se v rednih intervalih upoštevajo obrestne mere.

    Formula za polletne obrestne obresti

    Naj bo vložena glavnica P in obrestna mera R % na leto, ki se sešteva polletno za 't' let

    Kot sestavlja se polletno, glavnica se spremeni ob koncu 6 mesecev, in do takrat zaslužene obresti se prištejejo k glavnici in potem to postane nova glavnica. Podobno se izračuna končni znesek.

    Vemo,

    obrestna mera = R% na leto, polletno

    stopnja = (R/2) %

    čas je t let, vemo, da je t let 2t pol leta.

    zdaj,

    A = P (1 + R/200) 2t

    CI = A – P

    Formula za četrtletne obrestne obresti

    Naj bo vložena glavnica P in obrestna mera R % na leto, ki se sešteva četrtletno t let.

    Kot sestavlja se četrtletno, glavnica se spremeni ob koncu 3 mesecev, in do takrat zaslužene obresti se prištejejo k glavnici in potem to postane nova glavnica. Podobno se izračuna končni znesek.

    vemo,

    obrestna mera = R% na leto, izračunana četrtletno

    stopnja = (R/4)%

    čas je t let, vemo, da je t let 4t četrtine.

    zdaj,

    A = P(1 + R/400) 4t

    CI = A – P

    Preverite: Formula za četrtletne obrestne obresti

    nastavitev poti python

    Formula za mesečne obrestne obresti

    Če se obresti obračunavajo mesečno, bo število obresti 12-krat, obresti vsak mesec pa bodo znašale 1/12 letnih obresti. Zato je formula za mesečne obrestne obresti podana kot

    A = P[1 + (R/1200)] 12t

    CI = A – P

    Preverite: Formula za mesečne obrestne obresti

    Formula za dnevne obrestne obresti

    Če se obresti obračunavajo dnevno, potem.

    Nova obrestna mera bo R/365 %

    n = 365

    Zato je formula za dnevne obrestne obresti podana kot

    A = P[1 + (R/36500)] 365t

    CI = A – P

    Formula za stopnjo periodičnega mešanja

    Skupni znesek, vključno z glavnico P in obrestno mero CI, je podan z:

    A = P[1 + (r/n)] nt

    kje,

    • P = glavni
    • A = končni znesek
    • r = letna obrestna mera
    • n = kolikokrat se obresti sestavljajo
    • t = Čas (v letih)

    Tako so obrestne mere:

    CI = A – P

    Pravilo 72

    Pravilo 72 je formula, ki se uporablja za oceno, v koliko letih se naš denar podvoji, če se letno poveča. Za primer , če je naš denar vložen pri r % letno, potem traja 72/r let, da se naš denar podvoji.

    Ta izračun je uporaben tudi za izračun napihnjene vrednosti našega denarja, to pomeni, da v koliko letih se vrednost našega sredstva prepolovi, če se letno amortizira.

    Formula pravila 72

    Naslednja formula se uporablja za približno število let, v katerih se naša naložba podvoji.

    N = 72 / r

    kje,

    • N je približno število let, v katerih se naš denar podvoji
    • r je stopnja, po kateri se naš denar letno sestavi

    Primer pravila 72

    Recimo, da je Kabir vložil 10.00.000 rupij v dolžniški sklad, ki daje 8-odstotni donos. Ugotovite, v koliko letih se njegov denar podvoji, če se poveča letno.

    Z uporabo zgornje formule: N = 72/8 = 9 let

    torej traja 9 let, da se Kabirjev denar podvoji.

    Obrestne obresti zaporednih let

    Če imamo enako vsoto in enako obrestno mero. C.I. določenega leta je vedno več kot C.I prejšnjega leta. (IZ 3. leta je večji od IZ 2. leta). Razlika med CI za kateri koli dve zaporedni leti so obresti enega leta na CI prejšnjega leta.

    C.I 3. letnika – C.I 2. leta = C.I 2. letnika × r × 1/100

    imeof

    Razlika med zneski katerih koli dveh zaporednih let je obrest enega leta na znesek prejšnjega leta.

    Znesek 3. leta – Znesek 2. leta = Znesek 2. leta × r × 1/100

    Ključni rezultati

    Ko imamo enako vsoto in enako stopnjo ,

    C.I za n-to leto = C.I za (n – 1) leto + obresti za eno leto na C.I za (n – 1) leto

    Formula za neprekinjeno obrestno mero

    Formula za neprekinjeno združevanje se uporablja v Finance za izračun končne vrednosti naložbe, ki je podvržena neprekinjenemu združevanju v različnih obdobjih in se vrednost dodaja skozi čas. Formula za neprekinjeno mešanje je podana kot

    Končna vrednost = sedanja vrednost × e rt

    kje,

    • r je obrestna mera
    • t je čas

    Nauči se več, Formula neprekinjenega mešanja

    Nekatere druge uporabe obrestnih obresti

    Rast: To se uporablja predvsem za rast, če so panoge povezane.

    Proizvodnja po n letih = začetna proizvodnja × (1 + r/100) n

    Amortizacija: Ko se stroški izdelka vsako leto zmanjšajo za r%, potem je njegova vrednost po n letih

    Sedanja vrednost × (1 + r/100) n

    Težave s prebivalstvom: Ko prebivalstvo mesta, mesta ali vasi narašča z določeno stopnjo na leto.

    Prebivalstvo po n letih = sedanje prebivalstvo × (1 + r/100) n

    Razlika med sestavljenimi in navadnimi obrestmi

    Razliko med sestavljenimi in preprostimi obrestmi lahko izveste spodaj v tem članku

    Sestavljene obresti proti navadnim obrestim

    Obrestne obresti (CI)

    Enostavne obresti (SI)

    CI so obresti, ki se obračunajo tako na glavnico kot na predhodno zaslužene obresti.SI so obresti, ki se obračunavajo samo od glavnice.
    Za isto načelo, stopnjo in časovno obdobje CI> DA Za isto načelo, stopnjo in časovno obdobje JA

    Formula za CI je

    A = P(1 + R/100) T

    CI = A – P

    Formula za SI je

    ČE = (P×R×T) / 100

    Primeri sestavljenih obresti

    Nekaj ​​primerov formul za obrestne mere je,

    Primer 1: Poiščite obrestne obresti, ko je glavnica = 6000 Rs, obrestna mera = 10 % na leto in čas = 2 leti.

    rešitev:

    Obresti za prvo leto = (6000 × 10 × 1)/100 = 600

    Znesek ob koncu prvega leta = 6000 + 600 = 6600

    Obresti za drugo leto = (6600 × 10 × 1) / 100 = 660

    Znesek ob koncu drugega leta = 6600 + 660 = 7260

    Obrestne obresti = 7260 – 6000 = 1260

    Primer 2: Kolikšne bodo obrestne mere na 8000 Rs čez dve leti, ko bo obrestna mera 2 % na leto?

    rešitev:

    podano,

    • Glavni P = 8000
    • Stopnja r = 2%
    • Čas = 2 leti

    po formuli

    A = P (1 + R/100) n

    A = 8000 (1 + 2/100)2= 8000 (102/100)2

    A = 8323

    Sestavljene obresti = A – P = 8323 – 8000 = 323 Rs

    Primer 3: Hari je položil Rs. 4000 pri finančni družbi za 2 leti s obrestmi 5 % na leto. Kakšne so obrestne mere, ki jih Rohit dobi po 2 letih?

    rešitev:

    podano,

    • Glavni P = 4000
    • Stopnja r = 5%
    • Čas = 2 leti

    Po formuli,

    A = P (1 + R/100)n

    A = 4000 (1 + 5/100)2

    A = 4000 (105/100)2

    A = 4410

    Sestavljene obresti = A – P = 4410 – 4000 = 410

    Primer 4: Poiščite obrestno mero za Rs. 2000 po stopnji 4 % letno za 1,5 leta. Kdaj se obresti obračunavajo polletno?

    rešitev:

    podano,

    • Glavni p = 2000
    • Stopnja r = 4 %
    • Čas = 1,5 (tj. 3 pol leta)

    po formuli,

    A = P (1 + R/200) 2n

    np.edinstveno

    A = 2000 (1 + 4/200) 3

    A = 2000 (204/200) 3

    A = 2122

    Sestavljene obresti = A – P = 2122 – 2000 = 122

    Primer 5: Kakšne so obrestne mere na 10000 za eno leto po stopnji 20 % letno, če se obresti obračunavajo četrtletno?

    rešitev:

    podano,

    • Glavnica P = 10000 Rs
    • Stopnja R = 12 % (12/4 = 3 % na četrtletje leta)
    • Čas = 1 leto (1 × 4 = 4 četrtletja)

    Po formuli,

    A = P (1 + R/100) n

    A = 10000 (1 + 3/100) 4

    A = 10000 (103/100) 4

    A = 11255

    Sestavljene obresti = A – P = 11255 – 10000 = 1255

    Primer 6: Poiščite obrestne obresti po stopnji 5 % na leto za 2 leti na tisto glavnico, ki v 2 letih po stopnji 5 % na leto da Rs. 400 kot navadne obresti.

    rešitev:

    podano,

    • Enostavne obresti ČE = 400
    • Stopnja R = 5%
    • Čas T = 2 leti

    Po formuli,

    Preproste obresti = (P × T × R)/100

    ⇒ P = (SI × 100)/T × R

    P = (400 × 100)/2 × 5 Stopnja obrestne obresti = 5 %

    P = 40000/10 = 4000 Rs

    Čas = 2 leti

    Po formuli,

    A = P (1 + R/100)

    A = 4000 (1 + 5/100)

    A = 4410

    Sestavljene obresti = A – P = 4410 – 4000 = 410

    Primer 7: Poiščite obrestne obresti na 30000 Rs pri 7-odstotnih obrestnih obrestnih merah, ki se letno obračunavajo dve leti.

    rešitev:

    • Glavnica P = 30000 Rs
    • Stopnja R = 7%
    • Čas = 2 leti

    Po formuli,

    A = P (1 + R/100) n

    nizovne metode

    A = 30000 (1 + 7/100) 2

    A = 30000 (107/100) 2

    A = 34347

    Sestavljene obresti = A – P = 34347 – 30000 = 4347

    Povezano branje:

    • Dnevne obrestne obresti
    • Mesečne obrestne obresti
    • Rešitev za obrestne obresti razreda 8
    • Sestavljene obresti – vprašanja in odgovori o sposobnostih
    • Simple Interest

    Sestavljene obresti – vprašanja za vajo

    Različna praktična vprašanja o sestavljenih obrestih so,

    Q1. Poiščite znesek, ki ga je treba plačati po 3 letih, če je vsota 10000 posojena po stopnji 4 % letno.

    Q2. Ugotovite, da je treba obresti plačati po 1,5 letih, če posodite vsoto 2500 po obrestni meri 6 % polletno.

    Q3. Izračunajte obrestne obresti za izposojeni znesek 9000 po stopnji 5 % četrtletno za 15 mesecev.

    Q4. Izračunajte obrestne obresti za znesek 20000 posojenih po stopnji 12 % za 3 mesece, ki se obračunajo mesečno

    Sklenitev obrestnih obresti

    Obrestne obresti so a močan finančni koncept, ki omogoča, da naložbe ali posojila sčasoma rastejo ali se kopičijo. Za razliko od navadne obresti, ki izračunavajo samo obresti na začetni znesek glavnice, obrestno obrestovanje upošteva zaslužene obresti na začetno glavnico in vse akumulirane obresti iz prejšnjih obdobij.

    Sestavljene obresti – pogosta vprašanja

    Kaj pomenijo sestavljene obresti?

    Sestavljene obresti so obresti, izračunane na glavnico in prejšnje obresti, zaslužene v določenem časovnem obdobju.

    Kako izračunati obrestne obresti?

    Za izračun obrestne obresti se najprej izračuna končni znesek, nato pa se odšteje od glavnice, da se dobi končna obrestna mera. Znesek se izračuna po formuli,

    A = P(1 + R/100) t

    CI = A – P

    Ali so sestavljene obresti boljše od preprostih obresti za vlagatelje?

    Da, sestavljene obresti so za vlagatelje veliko boljše od preprostih obresti.

    Kaj je formula za obrestne obresti, če se obračunavajo dnevno?

    Recimo, da je dana glavnica P, obrestna mera R in časovni interval T let, potem je formula za obrestne obresti, ko se obračunavajo dnevno, naslednja:

    A = P(1 + R/365) {365 × T}

    Kakšna je razlika med CI in SI?

    Osnovna razlika med CI in SI je, da je SI obresti, zaračunane na znesek glavnice, medtem ko so CI obresti, zaračunane na znesek glavnice, pa tudi na obresti, nabrane na glavnico