Razvrstitev vedra je tehnika razvrščanja, ki vključuje delitev elementov v različne skupine ali vedra. Ta vedra so oblikovana z enakomerno porazdelitvijo elementov. Ko so elementi razdeljeni v vedra, jih je mogoče razvrstiti s katerim koli drugim algoritmom za razvrščanje. Na koncu so razvrščeni elementi zbrani skupaj na urejen način.
Algoritem za razvrščanje vedra:
Ustvari n prazna vedra (ali sezname) in naredite naslednje za vsak element polja arr[i].
- Vstavi arr[i] v vedro[n*array[i]]
- Razvrstite posamezne segmente z uporabo razvrščanja z vstavljanjem.
- Združi vse razvrščene vedre.
Kako deluje Bucket Sort?
Za uporabo razvrščanja vedra na vhodni matriki [0,78, 0,17, 0,39, 0,26, 0,72, 0,94, 0,21, 0,12, 0,23, 0,68] , sledimo tem korakom:
Korak 1: Ustvarite niz velikosti 10, kjer vsaka reža predstavlja vedro.

Ustvarjanje veder za razvrščanje
2. korak: Vstavite elemente v vedra iz vhodne matrike glede na njihov obseg.
Vstavljanje elementov v vedra:
java hashmap
- Vzemite vsak element iz vhodne matrike.
- Element pomnožite z velikostjo matrike vedra (v tem primeru 10). Na primer, za element 0,23 dobimo 0,23 * 10 = 2,3.
- Pretvori rezultat v celo število, kar nam da indeks vedra. V tem primeru se 2,3 pretvori v celo število 2.
- Vstavite element v vedro, ki ustreza izračunanemu indeksu.
- Ponovite te korake za vse elemente v vhodni matriki.
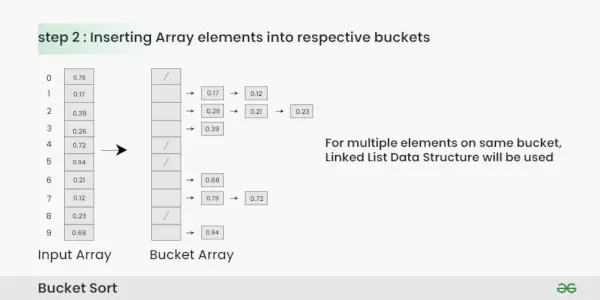
Vstavljanje elementov Array v ustrezna vedra
3. korak: Razvrstite elemente znotraj vsakega vedra. V tem primeru uporabljamo hitro razvrščanje (ali kateri koli stabilen algoritem za razvrščanje) za razvrščanje elementov znotraj vsakega vedra.
Razvrščanje elementov znotraj vsakega vedra:
- Uporabite stabilen algoritem za razvrščanje (npr. Bubble Sort, Merge Sort), da razvrstite elemente znotraj vsakega vedra.
- Elementi znotraj vsakega vedra so zdaj razvrščeni.
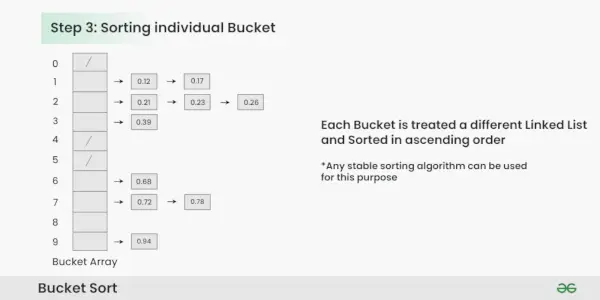
Razvrščanje posameznega vedra
4. korak: Zberite elemente iz vsakega vedra in jih postavite nazaj v prvotni niz.
Zbiranje elementov iz vsakega vedra:
nekaj za bfs
- Ponovite skozi vsako vedro po vrstnem redu.
- Vsak posamezen element iz vedra vstavite v izvirno matriko.
- Ko je element kopiran, se odstrani iz vedra.
- Ta postopek ponovite za vsa vedra, dokler niso zbrani vsi elementi.
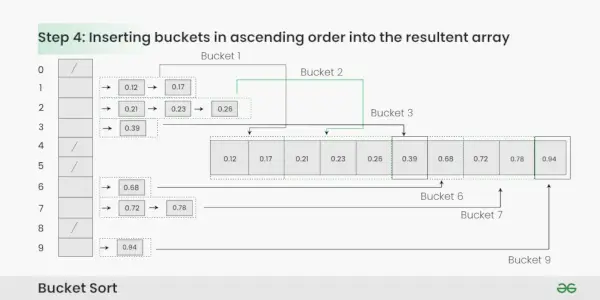
V nastalo matriko vstavite vedra v naraščajočem vrstnem redu
5. korak: Izvirna matrika zdaj vsebuje razvrščene elemente.
Končna razvrščena matrika z uporabo razvrščanja vedra za dani vnos je [0,12, 0,17, 0,21, 0,23, 0,26, 0,39, 0,68, 0,72, 0,78, 0,94].

Vrni razvrščeni niz
Implementacija algoritma za razvrščanje veder:
Spodaj je izvedba za Bucket Sort:
C++ #include #include using namespace std; // Insertion sort function to sort individual buckets void insertionSort(vector& bucket) { for (int i = 1; i< bucket.size(); ++i) { float key = bucket[i]; int j = i - 1; while (j>= 0 && vedro[j]> ključ) { vedro[j + 1] = vedro[j]; j--; } bucket[j + 1] = ključ; } } // Funkcija za razvrščanje arr[] velikosti n z uporabo bucket sort void bucketSort(float arr[], int n) { // 1) Ustvari vektor n praznih vederb[n]; // 2) Elemente matrike postavite v različna vedra za (int i = 0; i< n; i++) { int bi = n * arr[i]; b[bi].push_back(arr[i]); } // 3) Sort individual buckets using insertion sort for (int i = 0; i < n; i++) { insertionSort(b[i]); } // 4) Concatenate all buckets into arr[] int index = 0; for (int i = 0; i < n; i++) { for (int j = 0; j < b[i].size(); j++) { arr[index++] = b[i][j]; } } } // Driver program to test above function int main() { float arr[] = {0.897, 0.565, 0.656, 0.1234, 0.665, 0.3434}; int n = sizeof(arr) / sizeof(arr[0]); bucketSort(arr, n); cout << 'Sorted array is
'; for (int i = 0; i < n; i++) { cout << arr[i] << ' '; } return 0; }>
Java import java.util.ArrayList; import java.util.List; public class Main { // Insertion sort function to sort individual buckets public static void insertionSort(Listvedro) { for (int i = 1; i< bucket.size(); ++i) { float key = bucket.get(i); int j = i - 1; while (j>= 0 && bucket.get(j)> ključ) { bucket.set(j + 1, bucket.get(j)); j--; } bucket.set(j + 1, ključ); } } // Funkcija za razvrščanje arr[] velikosti n z uporabo bucket sort public static void bucketSort(float[] arr) { int n = arr.length; // 1) Ustvari n praznih seznamov veder[] vedra = nov ArrayList[n]; za (int i = 0; i< n; i++) { buckets[i] = new ArrayList(); } // 2) Put array elements in different buckets for (int i = 0; i < n; i++) { int bi = (int) (n * arr[i]); buckets[bi].add(arr[i]); } // 3) Sort individual buckets using insertion sort for (int i = 0; i < n; i++) { insertionSort(buckets[i]); } // 4) Concatenate all buckets into arr[] int index = 0; for (int i = 0; i < n; i++) { for (int j = 0; j < buckets[i].size(); j++) { arr[index++] = buckets[i].get(j); } } } // Driver program to test above function public static void main(String[] args) { float[] arr = {0.897f, 0.565f, 0.656f, 0.1234f, 0.665f, 0.3434f}; bucketSort(arr); System.out.println('Sorted array is:'); for (float num : arr) { System.out.print(num + ' '); } } }> Python def insertion_sort(bucket): for i in range(1, len(bucket)): key = bucket[i] j = i - 1 while j>= 0 in vedro[j]> ključ: vedro[j + 1] = vedro[j] j -= 1 vedro[j + 1] = ključ def bucket_sort(arr): n = len(arr) vedra = [[] for _ in range(n)] # Elemente polja postavi v različna vedra za num in arr: bi = int(n * num) buckets[bi].append(num) # Razvrsti posamezne vedre z uporabo razvrščanja z vstavljanjem za vedro v vedrih: insertion_sort (vedro) # Združi vse vedre v arr[] indeks = 0 za vedro v vedrih: za št v vedru: arr[indeks] = št. indeks += 1 arr = [0,897, 0,565, 0,656, 0,1234, 0,665, 0,3434] bucket_sort (arr) print('Razvrščena matrika je:') print(' '.join(map(str, arr)))> C# using System; using System.Collections.Generic; class Program { // Insertion sort function to sort individual buckets static void InsertionSort(Listvedro) { for (int i = 1; i< bucket.Count; ++i) { float key = bucket[i]; int j = i - 1; while (j>= 0 && vedro[j]> ključ) { vedro[j + 1] = vedro[j]; j--; } vedro [j + 1] = ključ; } } // Funkcija za razvrščanje arr[] velikosti n z uporabo bucket sort static void BucketSort(float[] arr) { int n = arr.Length; // 1) Ustvari n praznih seznamov veder[] vedra = nov seznam[n]; za (int i = 0; i< n; i++) { buckets[i] = new List(); } // 2) Elemente matrike postavite v različna vedra za (int i = 0; i< n; i++) { int bi = (int)(n * arr[i]); buckets[bi].Add(arr[i]); } // 3) Sort individual buckets using insertion sort for (int i = 0; i < n; i++) { InsertionSort(buckets[i]); } // 4) Concatenate all buckets into arr[] int index = 0; for (int i = 0; i < n; i++) { for (int j = 0; j < buckets[i].Count; j++) { arr[index++] = buckets[i][j]; } } } // Driver program to test above function static void Main(string[] args) { float[] arr = { 0.897f, 0.565f, 0.656f, 0.1234f, 0.665f, 0.3434f }; BucketSort(arr); Console.WriteLine('Sorted array is:'); foreach (float num in arr) { Console.Write(num + ' '); } } }> JavaScript function insertionSort(bucket) { for (let i = 1; i < bucket.length; ++i) { let key = bucket[i]; let j = i - 1; while (j>= 0 && vedro[j]> ključ) { vedro[j + 1] = vedro[j]; j--; } bucket[j + 1] = ključ; } } funkcija bucketSort(arr) { let n = arr.length; let buckets = Array.from({length: n}, () => []); // Postavi elemente matrike v različna vedra za (naj i = 0; i< n; i++) { let bi = Math.floor(n * arr[i]); buckets[bi].push(arr[i]); } // Sort individual buckets using insertion sort for (let i = 0; i < n; i++) { insertionSort(buckets[i]); } // Concatenate all buckets into arr[] let index = 0; for (let i = 0; i < n; i++) { for (let j = 0; j < buckets[i].length; j++) { arr[index++] = buckets[i][j]; } } } let arr = [0.897, 0.565, 0.656, 0.1234, 0.665, 0.3434]; bucketSort(arr); console.log('Sorted array is:'); console.log(arr.join(' '));> Izhod
Sorted array is 0.1234 0.3434 0.565 0.656 0.665 0.897>
Analiza kompleksnosti algoritma za razvrščanje veder:
Časovna zapletenost: O(n2),
- Če predpostavimo, da vstavljanje v vedro traja O(1) časa, potem koraka 1 in 2 zgornjega algoritma očitno vzameta O(n) časa.
- O(1) je zlahka mogoč, če za predstavitev vedra uporabimo povezan seznam.
- Korak 4 prav tako vzame O(n) časa, saj bo v vseh vedrih n elementov.
- Glavni korak za analizo je 3. korak. Ta korak v povprečju traja tudi O(n) časa, če so vsa števila enakomerno porazdeljena.
Pomožni prostor: O(n+k)
