V geometriji je kot bistvena meritev geometrijske oblike. Kot je definiran kot stopnja zasuka okoli presečišča med dvema črtama ali ravninama, ki sta potrebna, da se ena uskladi z drugo. Obstajajo različne vrste kotov, ki temeljijo na merjenju kota. Izmeri se v stopinjah ali radianih. Kot je oblika, ki jo tvorita dve črti ali žarka, ki se razlikujeta od skupne točke, imenovane vrh. Ko se dva žarka sekata, to je, ko se polpremice projicirajo s skupno končnico, nastane kot. Zdaj se skupne končne točke imenujejo oglišča, medtem ko so žarki znani kot roke.
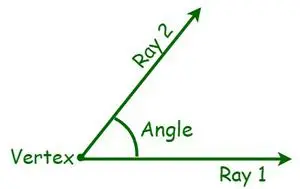
Vrste kotov

- Ostri kot: Ostri kot je kot, ki je večji od 0 stopinj in manjši od 90 stopinj, torej se giblje od 0° do 90° (oboje izključno).
- Pravi kot: Pravi kot se imenuje kot, ki meri natančno 90 stopinj.
- Topi kot: Topi kot je kot, ki je večji od 90 stopinj in manjši od 180 stopinj, torej se giblje od 90° do 180° (oboje izključno).
- Ravni kot: Ravni kot se imenuje kot, ki meri natančno 180 stopinj.
- Refleksni kot: Refleksni kot je kot, ki je večji od 180 stopinj in manjši od 360 stopinj, torej se giblje od 180° do 360° (oboje izključno).
- Celoten kot ali popolna rotacija: Celoten kot se imenuje kot, ki meri natančno 360 stopinj.
Obstajajo tudi druge vrste kotov, kot so komplementarni koti, dodatni koti ter sosednji in nesosednji koti.
- Komplementarni koti: Za dva kota pravimo, da sta komplementarna, če je njuna vsota pravi kot, to je 90°.
- Dodatni koti: Dva kota sta suplementna, če je njuna vsota enaka 180°.
- Sosednji koti: Dva kota sta sosednja, če imata skupno oglišče in krak.
- Nesosednji koti: Za dva kota pravimo, da nista sosednja, če nimata skupnega oglišča in skupnega kraka.
Formula za iskanje kotov
Obstajajo različne vrste formul za iskanje kota; nekatere od njih so formula osrednjega kota, formula dvojnega kota, formula polovičnega kota, formula sestavljenega kota, formula notranjega kota itd.
- Za določitev kota segmenta v krogu uporabljamo formulo središčnega kota.
- Za določitev manjkajočega kota v mnogokotniku uporabimo formulo za vsoto notranjih kotov.
- S trigonometričnimi razmerji poiščemo manjkajoči kot pravokotnega trikotnika.
- Za iskanje manjkajočega kota trikotnika, ki ni pravokoten, uporabljamo sinusni ali kosinusni zakon.
Ime formule | Formula | Kako najti neznani kot? |
|---|---|---|
| Formula osrednjega kota | θ =(s × 360°)/2prTukaj je s dolžina loka in r polmer kroga | Nadomestite vrednosti dolžine loka in polmera kroga, da določite kot segmenta, narejenega v krogu. |
| Formula vsote notranjih kotov | 180°(n-2)Tu je n število stranic mnogokotnika | Če želite določiti neznani notranji kot mnogokotnika, najprej izračunajte vsoto vseh notranjih kotov s to formulo in nato od rezultata odštejte vsoto vseh znanih kotov. |
| Trigonometrična razmerja | sin θ = nasprotna stran/hipotenuzacos θ = sosednja stranica/hipotenuzatan θ = nasprotna stran/sosednja stran | Odvisno od dveh strani pravokotnega trikotnika, ki sta na voljo, izberite eno od teh trigonometričnih razmerij, da poiščete neznani kot. delni derivat simbol lateks |
| Sinesov zakon | a/sin A = b/sin B = c/sin CTu so A, B in C notranji koti trikotnika, a, b in c pa njihove nasprotne stranice. | Ko poznamo dve stranici in nevključeni kot (ali) dva kota in nevključeno stranico, lahko sinusni zakon uporabimo za določitev neznanih kotov trikotnika. |
| Zakon kosinusov | a2= b2+ c2– 2bc cos Ab2= c2+ a2– 2ca cos Bc2= a2+ b2– 2ab cos CTu so A, B in C notranji koti trikotnika, a, b in c pa njihove nasprotne stranice. | Ko poznamo tri stranice (ali) dve strani in vključeni kot, lahko uporabimo kosinusni zakon za določitev neznanih kotov trikotnika. |
Vzorčna vprašanja
1. vprašanje: Poiščite kot pri oglišču B danega trikotnika z uporabo ene od trigonometričnih formul za iskanje kotov.

rešitev:
podano,
BC = 3 enote = sosednja stranica θ.
AC = 4 enote = nasprotna stran od θ.
V tem primeru poznamo nasprotno in sosednjo stran θ. Zato lahko za iskanje θ uporabimo formulo tangente.
⇒ tan θ = nasprotna stran/sosednja stran
⇒ tan θ = 4/3
⇒ θ = tan-1(4/3) ⇒ θ = 53,1°
Torej je kot pri točki B 53,1°.
Vprašanje 2: Poiščite kota pri ogliščih X in Y, če je ∠Z = 35° in x = 3 palca, y = 8 palcev in z = 3,5 palca.

rešitev:
podano,
∠Z = 35° in x = 6 palcev, y = 3 palcev in z = 3,5 palcev
Ker poznamo vse tri stranice in kot, lahko uporabimo formulo sinusnega pravila.
Iz formule sinusnega pravila imamo
x/sin X = y/sin Y = z/sin Z
zdaj,
y/sin Y = z/sin Z
strsep c⇒ 3/sin Y = 3,5/sin 35°
⇒ 3/brez Y = 3,5/0,574 {Ker je sin 35° = 0,574}
⇒ sin Y = 3 × (0,574/3,5) = 0,492
⇒ ∠Y = sin−1(0,492) = 29,47°
Vemo, da je vsota treh kotov v trikotniku 180°.
⇒ ∠X + ∠Y + ∠Z = 180°
⇒ ∠X + 29,47° + 35° = 180°
⇒ ∠X = 180° – 64,47° = 115,53°
Zato je ∠X = 115,53° in ∠Y = 29,47°.
3. vprašanje: Izračunajte peti notranji kot peterokotnika, če so štirje njegovi notranji koti 110°, 85°, 136° in 105°.
rešitev:
Število strani peterokotnika (n) = 5.
Zdaj je vsota vseh 5 notranjih kotov peterokotnika = 180 (n -2)°
= 180 (5 – 2)° = 540°.
Vsota danih 4 notranjih kotov = 110°+ 85°+ 136°+ in 105°= 436°.
Torej, peti notranji kot = 540° – 436° = 104°
Tako je peti notranji kot peterokotnika 104°.
4. vprašanje: Določite vrednost y in tudi mero kotov na dani sliki.

rešitev:
Iz podane slike lahko opazimo, da sta (4y – 6)° in (3y + 5)° komplementarna kota, tj. vsota (4y – 6)° in (3y + 5)° je 90 °.
⇒ (4y – 6)° + (3y + 5)° = 90°
⇒ (7y – 1)° = 90°
⇒ 7y = 90° + 1° = 91°
⇒ y = 91°/7 = 13°
Zdaj je (4y – 6)° = (4 × 13 – 6)° = (52 – 6)° = 46°
(3y + 5)° = (3 × 13 + 5)° = (39 + 5)° = 44°
5. vprašanje: Poiščite kot pri oglišču Q v danem trikotniku z eno od formul za iskanje kotov.

rešitev:
Podano je p = QR = 6 cm, q = PR = 9 cm in r = PQ = 7 cm.
Ker poznamo vse tri stranice in kot, lahko uporabimo formulo pravila kosinusa, da poiščemo oglišče Q kota.
⇒ q2= str2+ r2– 2pr cos Q
⇒ 92= 62+ 72– 2 (6) (7) cos Q
⇒ 81 = 36 + 49 – 84 cos Q
⇒ 81 = 85 – 84cos Q
⇒84 cos Q = 81 – 85
⇒ 84 cos Q = -4
⇒ cos Q = -4/84 = -1/21
⇒ ∠Q = cos-1(-1/21) = 92,72°
Zato je kot pri oglišču Q, ∠Q = 92,72°.
6. vprašanje: Izračunajte kot kroga, če je dolžina loka 12π in polmer 9 cm.
linux ukazi
rešitev:
podano,
Dolžina loka = 12π
Polmer (r) = 9 cm
Zdaj je formula kota:
⇒ θ = (s×360°)/2pr
⇒ θ = (12π × 360°)/(2π × 5)
⇒ θ =12 ×360°/10
⇒ θ = 240°
Torej je kot 240°.
