TRAPEZOIDNO PRAVILO: DEFINICIJA, FORMULA, PRIMERI IN POGOSTA VPRAŠANJA

Trapezoidno pravilo je eno izmed temeljnih pravil integracije, ki se uporablja za opredelitev osnovne definicije integracije. To je pogosto uporabljeno pravilo, trapezoidno pravilo pa se imenuje tako, ker daje površino pod krivuljo tako, da krivuljo razdeli na majhne trapeze namesto na pravokotnike.

Na splošno površino pod krivuljo poiščemo tako, da ploščino razdelimo na manjše pravokotnike in nato poiščemo vsoto vseh pravokotnikov, pri trapeznem pravilu pa se ploščina pod krivuljo razdeli na trapeze, nato pa se izračuna njihova vsota. Trapezoidno pravilo se uporablja za iskanje vrednosti določenih integralov v numerični analizi. To pravilo imenujemo tudi pravilo trapeza ali pravilo trapeza. Oglejmo si več o trapeznem pravilu, njegovi formuli in dokazu, primeru in drugih podrobnostih v tem članku.

Kaj je trapezoidno pravilo?

Trapezoidno pravilo je pravilo, ki se uporablja za iskanje vrednosti določenega integrala oblike^b∫_af(x) dx. Vemo, da je vrednost določenega integrala^b∫_af(x) dx je površina, ki je omejena pod krivuljo y = f(x) in osjo x v intervalu a in b na osi x. To ploščino izračunamo tako, da celotno ploščino razdelimo na več majhnih pravokotnikov in nato poiščemo njihovo vsoto.

V trapeznem pravilu, kot že ime pove, je površina pod krivuljo razdeljena na več trapezov, nato pa se ugotovi njihova vsota, da dobimo površino krivulje. Trapezoidno pravilo ne zagotavlja najboljšega približka površine pod krivuljo kot Simpsonovo pravilo, vendar je kljub temu njegov rezultat dovolj natančen in to pravilo je pogosto uporabljeno pravilo v računstvu.

Formula trapeznega pravila

Formula trapeznega pravila je formula, ki se uporablja za iskanje površine pod krivuljo. Zdaj, da bi našli površino pod krivuljo z uporabo trapeznega pravila,

Naj bo y = f(x) zvezna krivulja, definirana na zaprtem intervalu [a, b]. Sedaj razdelimo zaprti interval [a, b] na n enakih podintervalov, pri čemer ima vsak širino,

Δx = (b – a)/n

Tako, da

a = x₀ ₁ ₂<⋯ < x_n= b

Zdaj lahko z uporabo formule trapeznega pravila najdemo površino pod krivuljo kot,

∫^b_af(x) dx = površina pod krivuljo = (Δx/2) [y₀+ 2 (in₁+ in₂+ in₃+ ….. + in_n-1) + y_n]

kje, y₀, in₁, in₂,…. in_nso vrednosti funkcije pri x = 1, 2, 3, ….., n.

Izpeljava formule trapeznega pravila

Formula trapeznega pravila za izračun površine pod krivuljo se izpelje tako, da se površina pod krivuljo razdeli na več trapezov in se nato izračuna njihova vsota.

Izjava:

Naj bo f(x) zvezna funkcija, definirana na intervalu (a, b). Sedaj razdelimo intervale (a, b) na n enakih podintervalov, kjer je širina vsakega intervala,

Δx = (b – a)/n

tako da je a = x₀ ₁ ₂ ₃<…..< x_n= b

Potem je formula trapeznega pravila,

∫^b_af(x) dx ≈ △x/2 [f(x₀) + 2f(x₁) + 2f(x₂) +….2f(x_n-1) + f(x_n)]

kjer, x_jaz= a + i△x

Če n → ∞, daje R.H.S izraza določen integral $int_{a}^{b}f(x) dx$

Dokaz:

Ta formula je dokazana z razdelitvijo površine pod dano krivuljo, kot je prikazano na zgornji sliki, na različne trapeze. Prvi trapez ima višino Δx in dolžine vzporednih osnov so f(x₀) in f(x₁)

Ploščina prvega trapeza = (1/2) Δx [f(x₀) + f(x₁)]

Podobno je ploščina preostalih trapezov (1/2)Δx [f(x₁) + f(x₂)], (1/2)Δx [f(x₂) + f(x₃)], in tako naprej.

Zdaj lahko rečemo, da

∫^b_af(x) dx ≈ (1/2)Δx (f(x₀)+f(x₁) ) + (1/2)Δx (f(x₁)+f(x₂) ) + (1/2)Δx (f(x₂)+f(x₃) ) + … + (1/2)Δx (f(x_n-1) + f(x_n) )

Po poenostavitvi dobimo,

∫^b_af(x) dx≈ (Δx/2) (f(x₀)+2 f(x₁)+2 f(x₂)+2 f(x₃)+ … +2f(x_n-1) + f(x_n))

Tako je trapezoidno pravilo dokazano.

Kako uporabiti trapezoidno pravilo?

Trapezoidno pravilo najde površino pod krivuljo tako, da površino pod krivuljo razdeli na različne trapeze in nato poišče vsoto vseh trapezov. Trapezoidno pravilo ni popoln približek vrednosti določenega integrala, saj uporablja kvadratni približek.

Najti moramo vrednost določenega integrala, ∫^b_af(x) dx. Vrednost določenega integrala lahko izračunate z uporabo trapeznega pravila tako, da sledite spodnjim korakom,

Korak 1: Označite vrednost podintervalov n ter intervalov a in b.

2. korak: Poiščite širino podintervala (△x) z uporabo formule △x = (b – a)/n

3. korak: Vnesite vse vrednosti v formulo trapeznega pravila in poiščite približno ploščino dane krivulje, ki predstavlja določen integral ∫^b_af(x) dx

∫ ^b _a f(x) dx ≈ (Δx/2) (f(x ₀ )+2 f(x ₁ )+2 f(x ₂ )+2 f(x ₃ )+ … +2f(x _n-1 ) + f(x _n ))

kje, x _jaz = a + i△x

Sumacijski zapis trapeznega pravila

Vemo, da je površina trapeza v bistvu povprečje dolžin vzporednih stranic, pomnoženih z višino. Torej, v tem primeru razmislite o trapezu za i^thinterval,

$A_{i} = frac{f(x_{i}) + f(x_{i-1})}{2}Delta x$

Ker je skupna površina vsota vseh površin,

A = A₁+ A₂+ ….+ A_n

⇒ A = $vsota_{i = 1}^{i = n} A_{i}$

⇒ A = $vsota_{i = 1}^{i = n}frac{f(x_{i}) + f(x_{i-1})}{2}Delta x$

To se imenuje sigma zapis ali zapis seštevka vsot trapeza.

Riemann Sums

Riemann povzema delo na ideji o razdelitvi območja pod krivuljo na različne pravokotne dele. Z večanjem števila pravokotnikov postaja območje vedno bližje trenutnemu območju. Na spodnji sliki je funkcija f(x). Območje pod to funkcijo je razdeljeno na veliko pravokotnikov. Skupna površina pod krivuljo je vsota ploščin vseh pravokotnikov.

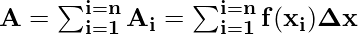
Upoštevajte, da se na zgornji sliki desni konec pravokotnikov dotika krivulje. To imenujemo desne Riemannove vsote.

V drugem primeru, ko se levi konec pravokotnikov dotika krivulje, kot je prikazano na spodnji sliki, se imenujejo leve Riemannove vsote.

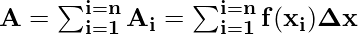
Recimo, da je Δx širina intervala, širina n je število intervalov, kot je navedeno zgoraj. Potem je površina krivulje, ki jo predstavlja vsota, podana z

$krepko{A = sum^{i = n}_{i = 1}A_{i} = sum^{i = n}_{i = 1}f(x_{i})Delta x}$

Vsota srednjih točk

Pri Riemannovi vsoti se levi ali desni konec pravokotnika dotika krivulje. V tem primeru se srednja točka pravokotnika dotika krivulje. Vse ostalo je enako kot Riemannove vsote. Spodnja slika prikazuje funkcijo f(x) in različne pravokotnike v vsotah srednjih točk.

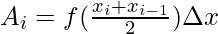
Recimo A_jazoznačuje območje i^thpravokotnik. Ploščina tega pravokotnika bo v tem primeru,

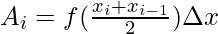
$A_{i} = f(frac{x_i + x_{i-1}}{2}) Delta x$

Zdaj bo skupna površina v zapisu seštevka podana z

$krepko{A = sum^{i = n}_{i = 1}A_{i} = sum^{i = n}_{i = 1}f(frac{x_{i} + x_{ i-1}}{2})Delta x}$

Preberi več,

Integracijske formule
Integracija po delih
Formula diferenciacije in integracije

Rešen primer na trapeznem pravilu

Primer 1: Poiščite območje, ki ga oklepa funkcija f(x) med x = 0 in x = 4 s 4 intervali.

f(x) = 4

rešitev:

Tu je a = 0, b = 4 in n = 4.
bellfordov algoritem

$Delta x= frac{b - a}{n} = Delta x = frac{4 - 0}{4} = Delta x = 1$

$x_{i} = a + iDelta x = x_{i} = 0 + i = x_{i} = i$

Trapezoidno pravilo za n = 4 je,

$T_n = frac{Delta x}{2}(f(x_0) + 2f(x_1) + 2f(x_2) + 2f(x_3) + f(x_4))$

Če nadomestimo vrednosti v tej enačbi,

$T_n = frac{Delta x}{2}(f(x_0) + 2f(x_1) + 2f(x_2) + 2f(x_3) + f(x_4)) = frac{1}{2}( f(0) + 2f(1) + 2f(2) + 2f(3) + f(4)) = frac{1}{2}(4 + 2(4) + 2(4) + 2(4) ) + 4) = 16$

Primer 2: Poiščite območje, ki ga oklepa funkcija f(x) med x = 0 in x = 3 s 3 intervali.

f(x) = x

rešitev:

Tu je a = 0, b = 3 in n = 3.

$Delta x= frac{b - a}{n} = Delta x = frac{3 - 0}{3} = Delta x = 1$

$x_{i} = a + iDelta x = x_{i} = 0 + i = x_{i} = i$

Trapezoidno pravilo za n = 3 je,

$T_n = frac{Delta x}{2}(f(x_0) + 2f(x_1) + 2f(x_2) + f(x_3))$

Če nadomestimo vrednosti v tej enačbi,

$T_n = frac{Delta x}{2}(f(x_0) + 2f(x_1) + 2f(x_2) + f(x_3)) Rightarrow T_n= frac{1}{2}(f( 0) + 2f(1) + 2f(2) + f(3)) Desna puščica T_n= frac{1}{2}(0 + 2 + 2(2) + 2(3)) Desna puščica T_n= frac{1}{2}(2 + 4 + 6) = 6$

Primer 3: Poiščite območje, ki ga oklepa funkcija f(x) med x = 0 in x = 2 z 2 intervaloma.

f(x) = 2x

rešitev:

Tu je a = 0, b = 2 in n = 2.

$Delta x= frac{b - a}{n} = Delta x = frac{2 - 0}{2} = Delta x = 1$

$x_{i} = a + iDelta x = x_{i} = 0 + i = x_{i} = i$

Trapezoidno pravilo za n = 2 je,

$T_n = frac{Delta x}{2}(f(x_0) + 2f(x_1) + f(x_2))$

Če nadomestimo vrednosti v tej enačbi,

$T_n = frac{Delta x}{2}(f(x_0) + 2f(x_1) + f(x_2)) Rightarrow T_n= frac{1}{2}(f(0) + 2f( 1) + f(2)) Desna puščica T_n= frac{1}{2}(0 + 2(2) + 1(4)) Desna puščica T_n= frac{1}{2}( 8) = 4$

Primer 4: Poiščite ploščino, ki jo oklepa funkcija f(x) med x = 0 do x = 3 s 3 intervali.

f(x) = x ²

rešitev:

Tu je a = 0, b = 3 in n = 3.

$Delta x= frac{b - a}{n} = Delta x = frac{3 - 0}{3} = Delta x = 1$

$x_{i} = a + iDelta x = x_{i} = 0 + i = x_{i} = i$

Trapezoidno pravilo za n = 3 je,

$T_n = frac{Delta x}{2}(f(x_0) + 2f(x_1) + 2f(x_2) + f(x_3))$

Če nadomestimo vrednosti v tej enačbi,

$T_n = frac{Delta x}{2}(f(x_0) + 2f(x_1) + 2f(x_2) + f(x_3)) Rightarrow T_n= frac{1}{2}(f( 0) + 2f(1) + 2f(2) + f(3)) Rightarrow T_n= frac{1}{2}(0 + 2(1) + 2(4) + 2(9)) Desna puščica T_n= frac{1}{2}(2 + 8 + 18) = 14$

Primer 5: Poiščite območje, ki ga oklepa funkcija f(x) med x = 0 in x = 4 s 4 intervali.

f(x) = x ³ + 1

rešitev:

Tu je a = 0, b = 4 in n = 4.

$Delta x= frac{b - a}{n} = Delta x = frac{4 - 0}{4} = Delta x = 1$

$x_{i} = a + iDelta x = x_{i} = 0 + i = x_{i} = i$

Trapezoidno pravilo za n = 4 je,

$T_n = frac{Delta x}{2}(f(x_0) + 2f(x_1) + 2f(x_2) + 2f(x_3) + f(x_4))$

Če nadomestimo vrednosti v tej enačbi,

$T_n = frac{Delta x}{2}(f(x_0) + 2f(x_1) + 2f(x_2) + 2f(x_3) + f(x_4)) Rightarrow T_n = frac{1}{ 2}(f(0) + 2f(1) + 2f(2) + 2f(3) + f(4)) Rightarrow T_n= frac{1}{2}(1 + 2(2) + 2(9) + 2(28) + (65) ) Desna puščica T_n= frac{1}{2}(1 + 4 + 18 + 56 + 65) Desna puščica T_n= 72$

Primer 6: Poiščite ploščino, ki jo oklepa funkcija f(x) med x = 0 in x = 4 s 4 intervali.

f(x) = e ^x

rešitev:

Tu je a = 0, b = 4 in n = 4.

$Delta x= frac{b - a}{n} = Delta x = frac{4 - 0}{4} = Delta x = 1$

$x_{i} = a + iDelta x = x_{i} = 0 + i = x_{i} = i$

Trapezoidno pravilo za n = 4 je,

$T_n = frac{Delta x}{2}(f(x_0) + 2f(x_1) + 2f(x_2) + 2f(x_3) + f(x_4))$

Če nadomestimo vrednosti v tej enačbi,

$T_n = frac{Delta x}{2}(f(x_0) + 2f(x_1) + 2f(x_2) + 2f(x_3) + f(x_4)) Rightarrow T_n= frac{1}{ 2}(f(0) + 2f(1) + 2f(2) + 2f(3) + f(4)) Rightarrow T_n= frac{1}{2}(e^0 + 2e + 2e ^2 + 2e^3 + e^4 ) Desna puščica T_n= frac{1}{2} + e + e^2 + e^3 + frac{e^4}{2}$

Uporaba trapeznega pravila

Numerična integracija:

Primarna uporaba trapeznega pravila je pri aproksimaciji določenih integralov. Uporablja se, ko je integracija funkcije zahtevna in je numerični pristop bolj izvedljiv. Trapezoidno pravilo je pogosto del naprednejših tehnik numerične integracije.

Fizika in tehnika:

V fiziki in tehniki lahko trapezoidno pravilo uporabimo za izračun količin, kot so premik, hitrost in pospešek. Na primer, ko se eksperimentalni podatki zbirajo v diskretnih časovnih intervalih, se lahko za oceno površine pod krivuljo uporabi trapezoidno pravilo, ki zagotavlja približek integrala.

Ekonomija in finance:

Trapezoidno pravilo je mogoče uporabiti pri finančnem modeliranju za oceno sedanje vrednosti prihodnjih denarnih tokov. To je še posebej uporabno pri analizi diskontiranih denarnih tokov (DCF), kjer je cilj izračunati neto sedanjo vrednost naložbe.

Statistika:

V statistiki lahko trapezoidno pravilo uporabimo za oceno površine pod funkcijami gostote verjetnosti ali kumulativnimi porazdelitvenimi funkcijami. To je še posebej uporabno v primerih, ko natančna oblika porazdelitve ni znana ali zapletena.

Pogosta vprašanja o trapeznem pravilu

V1: Kaj je trapezoidno pravilo?

odgovor:

Trapezoidno pravilo je pravilo, ki se uporablja za iskanje določenega integrala. Ploščino pod krivuljo razdeli na več trapezov, nato se najde njihova posamezna ploščina, nato pa se izračuna vsota, da se dobi vrednost določenega integrala.

V2: Kaj je formula trapeznega pravila?

odgovor:

Formula trapeznega pravila je,

∫ ^b _a f(x) dx = (Δx/2) (f(x ₀ )+2 f(x ₁ )+2 f(x ₂ )+2 f(x ₃ )+ … +2f(x _n-1 ) + f(x _n ))

V3: Zakaj se imenuje formula trapeznega pravila?

odgovor:

Formula trapeznega pravila se imenuje trapezno pravilo, ker razdeli ploščino pod krivuljo na več trapezov, nato pa se njihova ploščina izračuna z iskanjem vsote trapezov.

V4: Kakšna je razlika med trapeznim pravilom in Riemannovim pravilom vsot?

odgovor:

Glavna razlika med trapeznim pravilom in pravilom Riemannove vsote je v tem, da trapezno pravilo razdeli površino pod krivuljo kot trapeze in nato najde površino tako, da vzame njihovo vsoto, medtem ko Riemannova vsota razdeli površino pod krivuljo kot trapez in nato najde površino tako, da vzame njihovo vsoto.