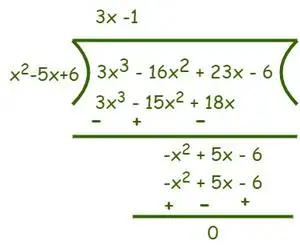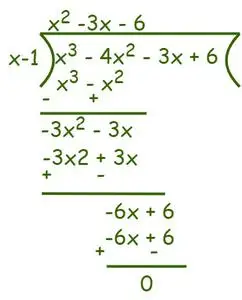Kubična enačba je matematična enačba, v kateri je polinom stopnje 3 enačen s konstanto ali drugim polinomom največje stopnje 2. Standardna predstavitev kubične enačbe je sekira ³ +bx ² +cx+d = 0 kjer so a, b, c in d realna števila. Nekaj ​​primerov kubične enačbe je x ³ – 4x ² + 15x – 9 = 0, 2x ³ – 4x ² = 0 itd.

Kazalo

• Definicija polinoma
• Stopnja enačbe
• Definicija kubične enačbe
• Kako rešiti kubične enačbe?
• Reševanje kubičnih enačb
• Reševanje kubične enačbe z uporabo faktorjev
• Reševanje kubične enačbe z grafično metodo
• Problemi, ki temeljijo na reševanju kubičnih enačb
• Vadbene naloge pri reševanju kubičnih enačb

Za učenje reševanja kubičnih enačb se moramo najprej naučiti polinomov, stopnje polinoma in drugih. V tem članku bomo podrobno spoznali polinome, polinomske enačbe, reševanje kubičnih enačb ali kako rešiti kubične enačbe in drugo.

Definicija polinoma

Polinom je definiran na naslednji način,

A polinom je algebraični izraz, v katerem je potenca spremenljivke nenegativno celo število. Splošna oblika polinoma je a₀xⁿ+ a₁x^n-1+ a₂x^n-2+… + a_n. Glede na največjo moč spremenljivke lahko polinom razvrstimo kot monom, binom, trinom in tako naprej.

Kaj je enačba?

Enačba je definirana na naslednji način,

Enačba je polinom, ki je enačen s številsko vrednostjo ali katerim koli drugim polinomom. Na primer, x + 2 je polinom, vendar je x + 2 = 5 enačba. Podobno je 2x + 3 = x + 1 prav tako enačba, medtem ko sta 2x + 3 in x + 1 posamično polinoma.

Stopnja enačbe

Opredelitev stopnje enačbe je navedena spodaj:

Stopnja enačbe je definirana kot največja moč, ki jo ima spremenljivka v enačbi.

Na podlagi stopnje enačbe lahko enačbo razvrstimo na naslednji način:

• Linearna enačba
• Kvadratna enačba
• Kubična enačba
• Bikvadratna enačba

Linearna enačba

Enačba, v kateri je največja moč spremenljivke 1, se imenuje linearna enačba.

• Na primer 3x +1 = 0

Kvadratni polinom

Enačba, v kateri je največja moč spremenljivke 2, je kvadratna enačba.

• Na primer 3x²+x+1 = 0

Kubična enačba

Enačba, v kateri je največja moč spremenljivke 3, se imenuje kubična enačba.

• Na primer 5x³+3x²+x+1 = 0

Bikvadratni polinom

Enačba, v kateri je največja moč spremenljivke 4, se imenuje bikvadratični polinom ali kvartični polinom.

• Na primer 5x⁴+4x³+3x²+2x+1 = 0

Definicija kubične enačbe

Kubična enačba je algebraična enačba, kjer je najvišja stopnja polinoma 3. Nekateri primeri kubičnih enačb so 5x³+3x²+x+1 = 0, 2x³+8 = x ⇒ 2x³-x+8 = 0 itd.

Splošna oblika kubične enačbe je,

sekira ³ + bx ² + cx + d = 0, a ≠ 0

Kje,

• a, b, in c so koeficienti spremenljivke in njihovi eksponenti ter d je konstanta in
• a, b, c in d so realna števila.

Kako rešiti kubične enačbe?

Kubična enačba je enačba tretje stopnje. Ima tri rešitve in jo je mogoče enostavno rešiti z upoštevanjem spodaj dodanih korakov,

Korak 1: Poiščite eno rešitev kubične enačbe z metodo zadetka in poskusa. Recimo, da imamo kubično enačbo P(x), nato poiščite za vsak x = a, P(a) = 0 tako, da vzamete, x = 0, ±1, ±2, ±3, … in tako.

2. korak: Ko dobimo P(a) = 0, poiščemo faktor (x – a) od P(x)

3. korak: P(x) delite z (x – a), da dobite kvadratno enačbo, recimo Q(x), s polinomskim deljenjem.

4. korak: Faktorizirajte kvadratno enačbo Q(x), da dobite faktorje kot (x – b) in (x – c).

5. korak: (x – a), (x – b) in (x – c) so faktorji P(x) in z reševanjem vsakega faktorja dobimo korene enačbe kot, a, b in c.

Več o, Delilni polinom

Reševanje kubičnih enačb

A Kubična enačba je mogoče rešiti na dva načina

• Tako, da jo reduciramo v kvadratno enačbo in jo nato rešimo s faktorizacijo ali kvadratno formulo
• Z grafično metodo

A Kubična enačba ima tri korenine. Te korenine so lahko resnične ali namišljene. Prav tako so lahko različni koreni ali dva enaka in en različen koren ter vsi trije enaki koreni.

Opozoriti je treba, da za vsako enačbo, vključno z Kubične enačbe , je treba enačbo vedno najprej urediti v standardno obliko, preden jo rešimo.

Na primer, če je dana enačba 2x²-5 = x + 4/x, potem moramo to preurediti v standardno obliko, tj. 2x³-x²-5x-4 = 0. Zdaj lahko rešimo enačbo s katero koli primerno metodo.

Reševanje kubične enačbe z uporabo faktorjev

Rešitev kubične enačbe z uporabo faktorskega izreka je razložena z uporabo spodaj dodanega primera,

Primer: Poiščite korenine enačbe f(x) = 3x ³ −16x ² + 23x − 6 = 0.

rešitev:

Podan izraz: f(x) = 3x³−16x²+ 23x − 6 = 0

Najprej faktorizirajte polinom, da dobite korenine

Ker je konstanta -6, so možni faktorji 1, 2, 3, 6

f(1) = 3 – 16 + 23 – 6 ≠ 0

f(2) = 24 – 64 + 46 – 6 = 0

f(3) = 81 – 144 + 69 – 6 = 0

f(6) = 648 – 576 + 138 – 6 ≠ 0

To vemo, glede na Faktorski izrek če je f(a) = 0, potem je (x-a) faktor f(x)

Torej sta (x – 2) in (x – 3) faktorja f(x). Zato bo produkt (x – 2) in (x – 3) tudi faktor f(x). Zdaj, da bi našli preostale faktorje, uporabite metodo dolgega deljenja in delite f(x) s produktom (x – 2) in (x – 3)

Zato je delitelj = (x – 2)(x – 3) = (x²– 5x + 6) in dividenda = 3x³−16x²+ 23x − 6. Zdaj delite, kot je prikazano spodaj,

tiger v primerjavi z levom

Po deljenju dobimo (3x- 1) kot količnik in ostanek je 0. Sedaj po Algoritem deljenja to vemo Dividenda = delitelj × količnik + preostanek.

⇒ f(x) = (3x³−16x²+ 23x − 6) = (x²– 5x + 6)(3x-1)

Ker je f(x) = 0

⇒ (x²– 5x + 6)(3x-1) = 0

⇒ x²– 5x + 6 = 0 ali 3x-1 = 0

Zdaj bomo vzeli 3x-1 = 0 ⇒ x = 1/3, saj že poznamo dva korena iz x²– 5x + 6, kar je 2 in 3

Torej,

Korenine danega Kubična enačba so 1/3, 2 in 3.

Reševanje kubične enačbe z grafično metodo

Kubična enačba se reši grafično, kadar dane enačbe ne morete rešiti z drugimi tehnikami. Torej potrebujemo natančno risbo dane kubične enačbe. Koreni enačbe so točke(-e), v katerih graf prečka os X, če je enačba v členih x in če je enačba v členih y, potem so koreni enačbe točke, v katerih graf reže Y-os.

Število realnih rešitev kubične enačbe je enako številu, kolikokrat graf kubične enačbe prečka os X.

Primer: Poiščite korenine enačbe f(x) = x ³ − 4x ² − 9x + 36 = 0, z grafično metodo.

rešitev:

Podan izraz: f(x) = x³− 4x²− 9x + 36 = 0.

Zdaj preprosto nadomestite naključne vrednosti za x v grafu za dano funkcijo:

x	-4	-3	-2	-1	0	1	2	3	4	5
f(x)	-56	0	19	40	36	24	10	0	0	16

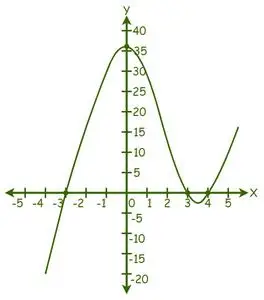
Vidimo lahko, da je graf presekal os X v 3 točkah, zato obstajajo 3 prave rešitve.

Iz grafa so rešitve: x = -3, x = 3 in x = 4.

Zato so koreni dane enačbe -3, 3 in 4.

Preberi več,

• Linearna enačba
• Reševanje kvadratne enačbe
• Faktoriziranje polinomov

Problemi, ki temeljijo na reševanju kubičnih enačb

Problem 1: Poiščite korenine f(x) = x ³ – 4x ² -3x + 6 = 0.

rešitev:

Podan izraz: f(x) = x³– 4x²-3x + 6 = 0.

Najprej faktorizirajte polinom, da dobite korenine.

Ker je konstanta +6, so možni faktorji 1, 2, 3, 6.

f(1) = 1 – 4 – 3 + 6 = 7 – 7 = 0

f(2) = 8 – 16 – 6 + 6 ≠ 0

f(3) = 27 – 36 – 9 + 6 ≠ 0

f(6) = 216 – 144 -18 + 6 = -48 ≠ 0

Torej, glede na Faktorski izrek (x – 1) je faktor dane enačbe. Za iskanje preostalih faktorjev uporabite metodo dolgega deljenja.

Po navedbah Algoritem deljenja lahko pišemo,

Torej, f(x) = x³– 4x²-3x + 6 = (x – 1) (x²– 3x – 6) = 0

⇒ (x – 1) = 0 ali (x²– 3x – 6) = 0

Vemo, da so korenine kvadratne enačbe os²+ bx + c = 0 so,

java delaj medtem

x = [-b ± √(b²-4ac)]/2a

Torej za (x²– 3x – 6) = 0

x = [3 ± √(3²– 4(1)(-6)]/2(1)

x = (3 ± √33)/2

Zato so koreni dane kubične enačbe 1, (3+√33)/2 in (3–√33)/2.

2. naloga: Poiščite korenine enačbe f(x) = 4x ³ – 10x ² + 4x = 0.

rešitev:

Podan izraz: f(x) = 4x³– 10x²+ 4x = 0

⇒ x (4x²– 10x + 4) = 0

⇒ x (4x²– 8x – 2x + 4) = 0

⇒ x(4x(x – 2) – 2(x – 2)) = 0

⇒ x (4x – 2) (x – 2) = 0

⇒ x = 0 ali 4x – 2 = 0, x – 2 = 0

⇒ x = 0 ali x = 1/2 ali x = 2

Zato so koreni dane enačbe 0, 1/2 in 2.

Naloga 3: Poišči korenine enačbe f(x) = x ³ + 3x ² + x + 3 = 0.

rešitev:

Podan izraz: f(x) = x³+ 3x²+ x + 3 = 0.

⇒ x²(x + 3) + 1 (x + 3) = 0

⇒ (x + 3) (x²+1) = 0

⇒ x + 3 = 0 ali x²+1 = 0

⇒ x = -3, ±i

Torej ima dana enačba realen koren, to je -3, in dva namišljena korena, to je ±i.

Naloga 4: Poišči korenine enačbe f(x) = x ³ – 7x ² – x + 7 = 0.

rešitev:

Podani izrazi,

blokiraj oglase na youtube android

f(x) = x³– 3x²– 5x + 7 = 0

Najprej faktoriziraj enačbo, f(x): x³– 3x²– 5x + 7= 0

Lahko se faktorizira v (x-7)(x+1)(x-1) = 0

Po faktoriziranju polinoma lahko najdemo korenine tako, da vsak faktor enačimo z nič. Na primer:

• x – 7 = 0, torej x = 7
• x + 1 = 0, torej x = -1
• x – 1 = 0, torej x = 1

Torej koreni enačbe f(x): x³– 3x²– 5x + 7 = 0 so

• x = 7
• x = -1
• x = 1

Problem 5: Poišči korenine enačbe f(x) = x ³ − 6x ² + 11x − 6 = 0, z uporabo grafične metode.

rešitev:

Podan izraz: f(x) = x³− 6x²+ 11x − 6 = 0.

Zdaj preprosto nadomestite naključne vrednosti za x v grafu za dano funkcijo:

x	1	2	3	4	5
f(x)	0	0	0	6	24

Vidimo lahko, da je graf presekal os X v 3 točkah, zato obstajajo 3 prave rešitve.

Iz grafa so rešitve: x = 1, x = 2 in x = 3.

Zato so koreni dane enačbe 1, 2 in 3.

Vadbene naloge pri reševanju kubičnih enačb

Spodaj so dodani različni praktični problemi, povezani s kubičnimi enačbami. Rešite te probleme, da boste v celoti razumeli koncept Kako rešiti kubično enačbo?

P1. Rešite kubično enačbo, 3x³+ 2x²– 11x + 7 = 0.

P2. Poiščite korenine kubične enačbe, 4x³– 12x²+ 17 = 0.

P3. Rešite kubično enačbo, x³+ 4x²– x + 3 = 0 z grafično metodo.

P4. Poiščite število, ki ustreza -9x³+ 11x²– 8x + 2 = 0.

Pogosta vprašanja o reševanju kubičnih enačb

1. Kaj so kubične enačbe?

Kubične enačbe so algebraične enačbe, v katerih je največja moč spremenljivke 3

2. Kako faktorizirate kubično enačbo?

Kubično enačbo lahko faktoriziramo na dva načina. Najprej tako, da vzamemo linearni izraz, ki je skupen iz dane kubične enačbe, nato pa bomo imeli linearni in kvadratni izraz kot produkt. To kvadratno enačbo je mogoče še faktorizirati, da dobimo vse faktorje. Druga metoda je iskanje ničle dane kubične enačbe z naključnimi vrednostmi. Vrednost, za katero dobimo, da je vrednost enačbe enaka nič, bo ena od ničel dane kubične enačbe. Zdaj z uporabo faktorskega izreka oblikujte linearni izraz, recimo x-a, in razdelite dano kubično enačbo s tem izrazom, kar bo dalo kvadratno enačbo kot količnik. To dobljeno kvadratno enačbo lahko še faktoriziramo, da dobimo vse faktorje.

3. Kako grafično rešite kubično enačbo?

Če želite rešiti kubično enačbo, grafično postavite naključne vrednosti za x v dano kubično enačbo in jo rešite, dobili boste vrednosti y. Dobljene vrednosti narišite na graf. Poiščite koordinate, pri katerih graf seka os x. Te koordinate so rešitev kubične enačbe.

4. Ali je mogoče vse kubične enačbe rešiti natančno?

Vsaka enačba z liho močjo mora imeti en pravi koren. Zato mora imeti kubična enačba vsaj en pravi koren, za razliko od kvadratne enačbe, kjer sta lahko oba korena namišljena, če je diskriminanta manjša od nič.

5. Ali ima lahko kubična enačba več rešitev?

Da, kubične enačbe imajo lahko več rešitev, saj ima lahko kubična enačba do tri različne realne korene.

6. Kaj mislite s stopnjo enačbe?

Največja moč, ki jo ima spremenljivka v enačbi, se imenuje stopnja polinoma.

7. Kakšna je razlika med polinomom in enačbo?

Polinom je preprosto algebraična enačba, v kateri je potenca spremenljivke nenegativno celo število. Ko je ta polinom enačen (=) s številsko vrednostjo ali drugim polinomom, se imenuje enačba.

8. Kaj je faktorski izrek za kubične enačbe?

Faktorski izrek pravi, da če je r koren (rešitev) kubične enačbe ax³+ bx²+ cx + d = 0, potem je x – r faktor enačbe.

9. Kaj pa, če s formulami ne najdem natančnih rešitev?

Če se zdi iskanje natančnih rešitev nemogoče, lahko uporabimo numerične metode, kot so iterativne metode (npr. Newtonova metoda), da približamo korenine enačbe.

Izvedite več o Newton Raphsonova metoda .