Graf kvantil-kvantil (graf q-q) je grafična metoda za ugotavljanje, ali nabor podatkov sledi določeni porazdelitvi verjetnosti ali pa dva vzorca podatkov prihajata iz istega prebivalstvo ali ne. Grafi Q-Q so še posebej uporabni za ocenjevanje, ali je nabor podatkov normalno porazdeljena ali če sledi kakšni drugi znani distribuciji. Običajno se uporabljajo v statistiki, analizi podatkov in nadzoru kakovosti za preverjanje predpostavk in ugotavljanje odstopanj od pričakovanih porazdelitev.
Kvantili in percentili
Kvantili so točke v nizu podatkov, ki delijo podatke v intervale, ki vsebujejo enake verjetnosti ali deleže celotne porazdelitve. Pogosto se uporabljajo za opis širjenja ali distribucije nabora podatkov. Najpogostejši kvantili so:
- Mediana (50. percentil) : Mediana je srednja vrednost nabora podatkov, če je urejen od najmanjšega do največjega. Nabor podatkov razdeli na dve enaki polovici.
- Kvartili (25., 50. in 75. percentil) : Kvartili razdelijo nabor podatkov na štiri enake dele. Prvi kvartil (Q1) je vrednost, pod katero pade 25 % podatkov, drugi kvartil (Q2) je mediana, tretji kvartil (Q3) pa vrednost, pod katero pade 75 % podatkov.
- Percentili : Percentili so podobni kvartilom, vendar razdelijo nabor podatkov na 100 enakih delov. Na primer, 90. percentil je vrednost, pod katero pade 90 % podatkov.
Opomba:
- Graf q-q je graf kvantilov prvega niza podatkov proti kvantilom drugega niza podatkov.
- Za referenčne namene je narisana tudi črta 45 %; Za če so vzorci iz iste populacije, potem so točke vzdolž te črte.
Normalna porazdelitev:
Normalna porazdelitev (alias Gaussova porazdelitev Bellova krivulja) je zvezna verjetnostna porazdelitev, ki predstavlja porazdelitev, pridobljeno iz naključno ustvarjenih realnih vrednosti.
. 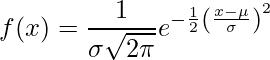

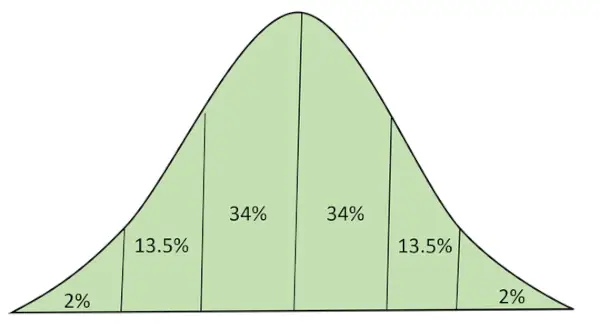
Normalna porazdelitev s površino pod krivuljo
Kako narisati graf Q-Q?
Če želite narisati graf kvantil-kvantil (Q-Q), lahko sledite tem korakom:
- Zberite podatke : Zberite nabor podatkov, za katerega želite ustvariti graf Q-Q. Prepričajte se, da so podatki numerični in predstavljajo naključen vzorec iz populacije, ki vas zanima.
- Razvrsti podatke : Razporedite podatke v naraščajočem ali padajočem vrstnem redu. Ta korak je bistvenega pomena za natančno izračunavanje kvantilov.
- Izberite teoretično porazdelitev : Določite teoretično porazdelitev, s katero želite primerjati svoj nabor podatkov. Pogoste izbire vključujejo normalno porazdelitev, eksponentno porazdelitev ali katero koli drugo porazdelitev, ki dobro ustreza vašim podatkom.
- Izračunajte teoretične kvantile : Izračunajte kvantile za izbrano teoretično porazdelitev. Če na primer primerjate z normalno porazdelitvijo, bi za iskanje pričakovanih kvantilov uporabili inverzno kumulativno porazdelitveno funkcijo (CDF) normalne porazdelitve.
- Plotovanje :
- Narišite razvrščene vrednosti nabora podatkov na os x.
- Narišite ustrezne teoretične kvantile na os y.
- Vsaka podatkovna točka (x, y) predstavlja par opazovanih in pričakovanih vrednosti.
- Povežite podatkovne točke, da vizualno preverite razmerje med naborom podatkov in teoretično porazdelitvijo.
Razlaga grafa Q-Q
- Če točke na grafu padajo približno vzdolž ravne črte, to nakazuje, da vaš nabor podatkov sledi domnevni porazdelitvi.
- Odstopanja od premice kažejo na odstopanja od predpostavljene porazdelitve, ki zahtevajo nadaljnje preiskave.
Raziskovanje podobnosti porazdelitve z grafom Q-Q
Raziskovanje podobnosti porazdelitve z uporabo grafov Q-Q je temeljna naloga v statistiki. Primerjava dveh nizov podatkov, da ugotovimo, ali izvirata iz iste distribucije, je ključnega pomena za različne analitične namene. Ko velja predpostavka o skupni porazdelitvi, lahko združevanje naborov podatkov izboljša natančnost ocenjevanja parametrov, na primer za lokacijo in obseg. Q-Q ploskve, okrajšava za kvantilne kvantilne ploskve, ponujajo vizualno metodo za ocenjevanje podobnosti porazdelitve. Na teh grafih so kvantili iz enega niza podatkov prikazani proti kvantilom iz drugega. Če so točke tesno poravnane vzdolž diagonalne črte, to kaže na podobnost med porazdelitvami. Odstopanja od te diagonalne črte kažejo na razlike v značilnostih porazdelitve.
Medtem ko so testi, kot je hi-kvadrat in Kolmogorov-Smirnov testi lahko ovrednotijo splošne razlike v distribuciji, Q-Q ploskve zagotavljajo niansirano perspektivo z neposredno primerjavo kvantilov. To omogoča analitikom, da zaznajo posebne razlike, kot so premiki v lokaciji ali spremembe v obsegu, ki morda niso razvidne samo iz formalnih statističnih testov.
Python implementacija Q-Q Plot
Python3
import> numpy as np> import> matplotlib.pyplot as plt> import> scipy.stats as stats> # Generate example data> np.random.seed(>0>)> data>=> np.random.normal(loc>=>0>, scale>=>1>, size>=>1000>)> # Create Q-Q plot> stats.probplot(data, dist>=>'norm'>, plot>=>plt)> plt.title(>'Normal Q-Q plot'>)> plt.xlabel(>'Theoretical quantiles'>)> plt.ylabel(>'Ordered Values'>)> plt.grid(>True>)> plt.show()> |
>
>
Izhod:
Q-Q graf
Tukaj, ker podatkovne točke približno sledijo ravni črti na grafu Q-Q, nakazuje, da je nabor podatkov skladen s predpostavljeno teoretično porazdelitvijo, za katero smo v tem primeru domnevali, da je normalna porazdelitev.
Prednosti ploskve Q-Q
- Prilagodljiva primerjava : Grafi Q-Q lahko primerjajo nize podatkov različnih velikosti brez ki zahteva enake velikosti vzorcev.
- Brezdimenzijska analiza : So brez dimenzij, zaradi česar so primerni za primerjavo naborov podatkov različne enote ali lestvice.
- Vizualna interpretacija : Zagotavlja jasno vizualno predstavitev porazdelitve podatkov v primerjavi s teoretično porazdelitvijo.
- Občutljiv na odstopanja : Preprosto zazna odstopanja od predpostavljenih porazdelitev, kar pomaga pri prepoznavanju neskladij podatkov.
- Diagnostično orodje : Pomaga pri ocenjevanju distribucijskih predpostavk, prepoznavanju izstopajočih vrednosti in razumevanju podatkovnih vzorcev.
Uporaba kvantilno-kvantilnega grafa
Graf kvantil-kvantil se uporablja za naslednje namene:
- Ocenjevanje distribucijskih predpostavk : Grafi Q-Q se pogosto uporabljajo za vizualno preverjanje, ali nabor podatkov sledi določeni porazdelitvi verjetnosti, kot je normalna porazdelitev. S primerjavo kvantilov opazovanih podatkov s kvantili predpostavljene porazdelitve je mogoče zaznati odstopanja od predpostavljene porazdelitve. To je ključnega pomena pri številnih statističnih analizah, kjer veljavnost distribucijskih predpostavk vpliva na točnost statističnih sklepov.
- Odkrivanje odstopanj : Izstopajoči podatki so podatkovne točke, ki znatno odstopajo od preostalega nabora podatkov. Grafi Q-Q lahko pomagajo prepoznati odstopanja z razkrivanjem podatkovnih točk, ki so daleč od pričakovanega vzorca porazdelitve. Izstopajoči se lahko pojavijo kot točke, ki odstopajo od pričakovane ravne črte na grafu.
- Primerjava distribucij : Grafe Q-Q lahko uporabite za primerjavo dveh nizov podatkov, da ugotovite, ali prihajata iz iste distribucije. To se doseže z risanjem kvantilov enega nabora podatkov proti kvantilom drugega nabora podatkov. Če točke padajo približno vzdolž ravne črte, to nakazuje, da sta oba niza podatkov vzeta iz iste porazdelitve.
- Ocenjevanje normalnosti : Grafi Q-Q so še posebej uporabni za ocenjevanje normalnosti nabora podatkov. Če podatkovne točke na grafu tesno sledijo ravni črti, to pomeni, da je nabor podatkov približno normalno porazdeljen. Odstopanja od črte kažejo na odstopanja od normalnosti, kar lahko zahteva nadaljnje preiskave ali neparametrične statistične tehnike.
- Validacija modela : Na področjih, kot sta ekonometrija in strojno učenje, se diagrami Q-Q uporabljajo za potrjevanje napovednih modelov. S primerjavo kvantilov opazovanih odzivov s kvantili, ki jih napoveduje model, lahko ocenimo, kako dobro se model ujema s podatki. Odstopanja od pričakovanega vzorca lahko kažejo na področja, kjer je treba model izboljšati.
- Kontrola kakovosti : Grafi Q-Q se uporabljajo v procesih nadzora kakovosti za spremljanje porazdelitve izmerjenih ali opazovanih vrednosti skozi čas ali med različnimi serijami. Odstopanja od pričakovanih vzorcev v ploskvi lahko signalizirajo spremembe v osnovnih procesih, kar spodbudi nadaljnje preiskave.
Vrste grafov Q-Q
Obstaja več vrst diagramov Q-Q, ki se običajno uporabljajo v statistiki in analizi podatkov, od katerih je vsaka primerna za različne scenarije ali namene:
- Normalna porazdelitev : Simetrična porazdelitev, kjer bi graf Q-Q pokazal točke približno vzdolž diagonalne črte, če se podatki držijo normalne porazdelitve.
- Desno poševna porazdelitev : Porazdelitev, kjer bi graf Q-Q prikazal vzorec, kjer opazovani kvantili odstopajo od ravne črte proti zgornjemu koncu, kar kaže na daljši rep na desni strani.
- Levo poševna porazdelitev : Porazdelitev, kjer bi graf Q-Q pokazal vzorec, kjer opazovani kvantili odstopajo od ravne črte proti spodnjemu koncu, kar kaže na daljši rep na levi strani.
- Premalo razpršena porazdelitev : Porazdelitev, pri kateri bi graf Q-Q pokazal opazovane kvantile, zbrane tesneje okoli diagonalne črte v primerjavi s teoretičnimi kvantili, kar kaže na manjšo varianco.
- Prekomerno razpršena distribucija : Porazdelitev, pri kateri bi graf Q-Q prikazal opazovane kvantile bolj razpršene ali odklonjene od diagonalne črte, kar kaže na večjo varianco ali disperzijo v primerjavi s teoretično porazdelitvijo.
Python3
import> numpy as np> import> matplotlib.pyplot as plt> import> scipy.stats as stats> # Generate a random sample from a normal distribution> normal_data>=> np.random.normal(loc>=>0>, scale>=>1>, size>=>1000>)> # Generate a random sample from a right-skewed distribution (exponential distribution)> right_skewed_data>=> np.random.exponential(scale>=>1>, size>=>1000>)> # Generate a random sample from a left-skewed distribution (negative exponential distribution)> left_skewed_data>=> ->np.random.exponential(scale>=>1>, size>=>1000>)> # Generate a random sample from an under-dispersed distribution (truncated normal distribution)> under_dispersed_data>=> np.random.normal(loc>=>0>, scale>=>0.5>, size>=>1000>)> under_dispersed_data>=> under_dispersed_data[(under_dispersed_data>>->1>) & (under_dispersed_data <>1>)]># Truncate> # Generate a random sample from an over-dispersed distribution (mixture of normals)> over_dispersed_data>=> np.concatenate((np.random.normal(loc>=>->2>, scale>=>1>, size>=>500>),> >np.random.normal(loc>=>2>, scale>=>1>, size>=>500>)))> # Create Q-Q plots> plt.figure(figsize>=>(>15>,>10>))> plt.subplot(>2>,>3>,>1>)> stats.probplot(normal_data, dist>=>'norm'>, plot>=>plt)> plt.title(>'Q-Q Plot - Normal Distribution'>)> plt.subplot(>2>,>3>,>2>)> stats.probplot(right_skewed_data, dist>=>'expon'>, plot>=>plt)> plt.title(>'Q-Q Plot - Right-skewed Distribution'>)> plt.subplot(>2>,>3>,>3>)> stats.probplot(left_skewed_data, dist>=>'expon'>, plot>=>plt)> plt.title(>'Q-Q Plot - Left-skewed Distribution'>)> plt.subplot(>2>,>3>,>4>)> stats.probplot(under_dispersed_data, dist>=>'norm'>, plot>=>plt)> plt.title(>'Q-Q Plot - Under-dispersed Distribution'>)> plt.subplot(>2>,>3>,>5>)> stats.probplot(over_dispersed_data, dist>=>'norm'>, plot>=>plt)> plt.title(>'Q-Q Plot - Over-dispersed Distribution'>)> plt.tight_layout()> plt.show()> |
>
>
Izhod:
Graf Q-Q za različne porazdelitve
primeri operacijskega sistema
