Predpogoj: Linearna regresija
Linearna regresija je algoritem strojnega učenja, ki temelji na nadzorovanem učenju. Izvaja nalogo regresije. Regresija modelira ciljno napovedno vrednost na podlagi neodvisnih spremenljivk. Večinoma se uporablja za ugotavljanje povezave med spremenljivkami in napovedovanjem. Različni regresijski modeli se razlikujejo glede na – vrsto razmerja med odvisnimi in neodvisnimi spremenljivkami, ki jih upoštevajo, in število uporabljenih neodvisnih spremenljivk. Ta članek bo pokazal, kako uporabiti različne knjižnice Python za implementacijo linearne regresije na dani niz podatkov. Predstavili bomo binarni linearni model, saj si ga bomo lažje predstavljali. V tej predstavitvi bo model za učenje uporabil Gradient Descent. O tem se lahko naučite tukaj.
Korak 1: Uvoz vseh zahtevanih knjižnic
Python3
import> numpy as np> import> pandas as pd> import> seaborn as sns> import> matplotlib.pyplot as plt> from> sklearn>import> preprocessing, svm> from> sklearn.model_selection>import> train_test_split> from> sklearn.linear_model>import> LinearRegression> |
>
>
2. korak: Branje nabora podatkov:
Python3
df>=> pd.read_csv(>'bottle.csv'>)> df_binary>=> df[[>'Salnty'>,>'T_degC'>]]> > # Taking only the selected two attributes from the dataset> df_binary.columns>=> [>'Sal'>,>'Temp'>]> #display the first 5 rows> df_binary.head()> |
>
>
Izhod:
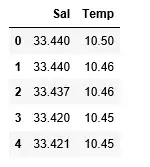
3. korak: Raziskovanje razpršenosti podatkov
Python3
java proti c++
#plotting the Scatter plot to check relationship between Sal and Temp> sns.lmplot(x>=>'Sal'>, y>=>'Temp'>, data>=> df_binary, order>=> 2>, ci>=> None>)> plt.show()> |
>
>
Izhod:

4. korak: Čiščenje podatkov
Python3
# Eliminating NaN or missing input numbers> df_binary.fillna(method>=>'ffill'>, inplace>=> True>)> |
>
>
5. korak: Usposabljanje našega modela
Python3
X>=> np.array(df_binary[>'Sal'>]).reshape(>->1>,>1>)> y>=> np.array(df_binary[>'Temp'>]).reshape(>->1>,>1>)> > # Separating the data into independent and dependent variables> # Converting each dataframe into a numpy array> # since each dataframe contains only one column> df_binary.dropna(inplace>=> True>)> > # Dropping any rows with Nan values> X_train, X_test, y_train, y_test>=> train_test_split(X, y, test_size>=> 0.25>)> > # Splitting the data into training and testing data> regr>=> LinearRegression()> > regr.fit(X_train, y_train)> print>(regr.score(X_test, y_test))> |
>
>
Izhod:

6. korak: Raziskovanje naših rezultatov
Python3
y_pred>=> regr.predict(X_test)> plt.scatter(X_test, y_test, color>=>'b'>)> plt.plot(X_test, y_pred, color>=>'k'>)> > plt.show()> # Data scatter of predicted values> |
>
>
Izhod:

Nizka ocena natančnosti našega modela kaže, da se naš regresivni model ne ujema dobro z obstoječimi podatki. To nakazuje, da naši podatki niso primerni za linearno regresijo. Včasih pa lahko nabor podatkov sprejme linearni regresor, če upoštevamo le njegov del. Preverimo to možnost.
7. korak: Delo z manjšim naborom podatkov
Python3
df_binary500>=> df_binary[:][:>500>]> > # Selecting the 1st 500 rows of the data> sns.lmplot(x>=>'Sal'>, y>=>'Temp'>, data>=> df_binary500,> >order>=> 2>, ci>=> None>)> |
kako centrirati sliko na css
>
>
Izhod:

Vidimo že, da prvih 500 vrstic sledi linearnemu modelu. Nadaljujte z enakimi koraki kot prej.
Python3
df_binary500.fillna(method>=>'fill'>, inplace>=> True>)> > X>=> np.array(df_binary500[>'Sal'>]).reshape(>->1>,>1>)> y>=> np.array(df_binary500[>'Temp'>]).reshape(>->1>,>1>)> > df_binary500.dropna(inplace>=> True>)> X_train, X_test, y_train, y_test>=> train_test_split(X, y, test_size>=> 0.25>)> > regr>=> LinearRegression()> regr.fit(X_train, y_train)> print>(regr.score(X_test, y_test))> |
>
>
Izhod:

Python3
y_pred>=> regr.predict(X_test)> plt.scatter(X_test, y_test, color>=>'b'>)> plt.plot(X_test, y_pred, color>=>'k'>)> > plt.show()> |
>
>
Izhod:

8. korak: Ocenjevalne metrike za regresijo
Na koncu preverimo delovanje modela linearne regresije s pomočjo metrike vrednotenja. Za regresijske algoritme široko uporabljamo metriki mean_absolute_error in mean_squared_error za preverjanje učinkovitosti modela.
Python3
from> sklearn.metrics>import> mean_absolute_error,mean_squared_error> > mae>=> mean_absolute_error(y_true>=>y_test,y_pred>=>y_pred)> #squared True returns MSE value, False returns RMSE value.> mse>=> mean_squared_error(y_true>=>y_test,y_pred>=>y_pred)>#default=True> rmse>=> mean_squared_error(y_true>=>y_test,y_pred>=>y_pred,squared>=>False>)> > print>(>'MAE:'>,mae)> print>(>'MSE:'>,mse)> print>(>'RMSE:'>,rmse)> |
>
>
Izhod:
MAE: 0.7927322046360309 MSE: 1.0251137190180517 RMSE: 1.0124789968281078>
