Poznamo a drevo je nelinearna podatkovna struktura. Nima omejitev glede števila otrok. AKaj je popolno binarno drevo?

Popolno binarno drevo je posebna vrsta binarnega drevesa, kjer so vse ravni drevesa popolnoma zapolnjene, razen vozlišč najnižje ravni, ki so zapolnjena čim bolj levo.

Popolno binarno drevo

Nekaj ​​terminologije popolnega binarnega drevesa:

• Root – Vozlišče, v katerem noben rob ne prihaja iz nadrejenega. Primer - vozlišče A
• Otrok – Vozlišče, ki ima nekaj vhodnega roba, se imenuje otrok. Primer – vozlišča B, F so podrejena vozlišča A oziroma C.
• brat in sestra – Vozlišča, ki imajo istega starša, so sorodna. Primer - D, E sta brata in sestra, saj imata istega starša B.
• Stopnja vozlišča – Število otrok posameznega starša. Primer – stopnja A je 2 in stopnja C je 1. Stopnja D je 0.
• Notranja/zunanja vozlišča – Listna vozlišča so zunanja vozlišča, nelistna vozlišča pa notranja vozlišča.
• Raven – Preštejte vozlišča na poti, da dosežete ciljno vozlišče. Primer – raven vozlišča D je 2, saj vozlišči A in B tvorita pot.
• Višina – Število robov za dosego ciljnega vozlišča, koren je na višini 0. Primer – Višina vozlišča E je 2, saj ima dva robova od korena.

Lastnosti popolnega binarnega drevesa:

• Za popolno binarno drevo pravimo, da je pravilno binarno drevo, kjer imajo vsi listi enako globino.
• V celotnem binarnem drevesu število vozlišč v globini d je 2 ^d .
• V popolnem binarnem drevesu z n vozlišča višina drevesa je log(n+1) .
• Vse stopnje razen zadnje stopnje so popolnoma polni.

Popolno binarno drevo v primerjavi s popolnim binarnim drevesom:

Binarno drevo višine 'h' z največjim številom vozlišč je a popolna binarno drevo.
Za določeno višino h , je največje število vozlišč 2 ^h+1 -1 .

A popolna binarno drevo višine h je popolno binarno drevo do višine h-1 in v elementu zadnje ravni so shranjeni v vrstnem redu od leve proti desni.

Primer 1:

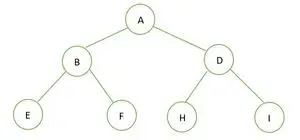
Binarno drevo

Višina danega binarnega drevesa je 2 in največje število vozlišč v tem drevesu je n= 2^h+1-1 = 2²⁺¹-1 = 2³-1 = 7 .
Zato lahko sklepamo, da je popolno binarno drevo .
Zdaj za popolno binarno drevo, je polno do višine h-1 tj.; 1, elementi zadnje ravni pa so shranjeni v vrstnem redu od leve proti desni. Zato je tudi popolno binarno drevo. Tukaj je predstavitev elementov, ko so shranjeni v matriki

Element, shranjen v nizu nivo za nivojem

V matriki so vsi elementi shranjeni neprekinjeno.

Primer 2:

xor v c++

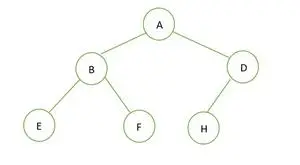
Binarno drevo

Višina podanega binarnega drevesa je 2 in največje število vozlišč, ki bi moralo biti tam, je 2^h+1– 1 = 2²⁺¹– 1 = 2³– 1 = 7 .
Toda število vozlišč v drevesu je 6 . Zato je ni popolno binarno drevo .
Zdaj za popolno binarno drevo, je polno do višine h-1 tj.; 1 in element zadnje ravni sta shranjena v vrstnem redu od leve proti desni. Zato je to a popolno binarno drevo . Shranite element v matriko in bo kot;

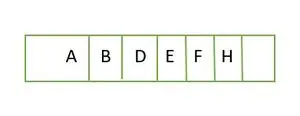
Element, shranjen v nizu nivo za nivojem

Primer 3:

np.edinstveno

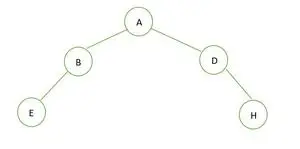
Binarno drevo

Višina binarnega drevesa je 2 in največje število vozlišč, ki so lahko tam, je 7, vendar je vozlišč le 5, zato je ni popolno binarno drevo .
V primeru popolnega binarnega drevesa vidimo, da elementi na zadnji ravni niso zapolnjeni od leve proti desni. Tako je ni popolno binarno drevo .

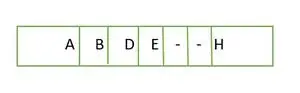
Element, shranjen v nizu nivo za nivojem

Elementi v nizu niso zvezni.

Celotno binarno drevo proti popolnemu binarnemu drevesu:

Za polno binarno drevo ima vsako vozlišče 2 otroka ali 0 otrok.

Primer 1:

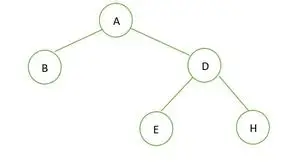
Binarno drevo

V danem binarnem drevesu ni vozlišča s stopnjo 1, 2 ali 0 otrok za vsako vozlišče, zato je polno binarno drevo .

Za popolno binarno drevo so elementi shranjeni v nivoju za nivojem in ne na skrajni levi strani v zadnjem nivoju. Zato je to ni popolno binarno drevo . Predstavitev niza je:

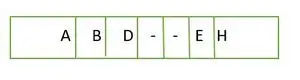
Element, shranjen v nizu nivo za nivojem

Primer 2:

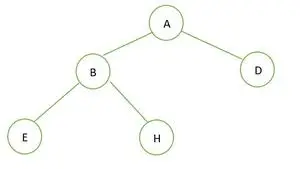
Binarno drevo

V danem binarnem drevesu ni vozlišča s stopnjo 1. Vsako vozlišče ima stopnjo 2 ali 0. Zato je polno binarno drevo .

Za popolno binarno drevo so elementi shranjeni po stopnjah in zapolnjeni od skrajne leve strani zadnje ravni. Zato ta a popolno binarno drevo . Spodaj je matrična predstavitev drevesa:

Element, shranjen v nizu nivo za nivojem

Primer 3:

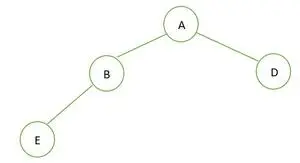
Binarno drevo

V danem binarnem drevesu ima vozlišče B stopnjo 1, ki krši lastnost polnega binarnega drevesa, zato je ni polno binarno drevo

stavek bash if

Za popolno binarno drevo so elementi shranjeni po nivojih in se polnijo od skrajne leve strani zadnje ravni. Zato je to a popolno binarno drevo . Matrična predstavitev binarnega drevesa je:

Element, shranjen v nizu nivo za nivojem

Primer 4:

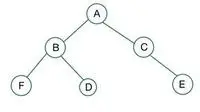
binarno drevo

V danem binarnem drevesu ima vozlišče C stopnjo 1, ki krši lastnost polnega binarnega drevesa, zato je ni polno binarno drevo

Za popolno binarno drevo so elementi shranjeni po nivojih in se polnijo od skrajne leve strani zadnje ravni. Tukaj vozlišče E krši pogoj. Zato je to ni popolno binarno drevo .

Izdelava popolnega binarnega drevesa:

Poznamo a popolno binarno drevo je drevo, v katerem razen zadnje ravni (recimo l )vsa druga raven ima ( 2l ) vozlišča in vozlišča so poravnana od leve proti desni strani.
Predstavi se lahko z uporabo matrike. Če je nadrejeni, je to indeks jaz torej je levi otrok pri 2i+1 in pravi otrok je pri 2i+2 .

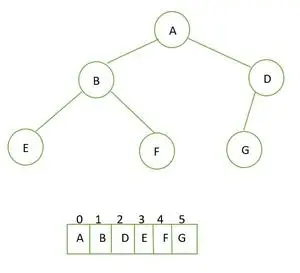
Popolno binarno drevo in njegova matrična predstavitev

Algoritem:

10 na potenco števila 6

Za ustvarjanje a Popolno binarno drevo , potrebujemo a Korak 1: Inicializirajte koren z novim vozliščem, ko je drevo prazno.

2. korak: Če drevo ni prazno, dobite sprednji element

• Če sprednji element nima levega otroka, nastavite levega otroka na novo vozlišče
• Če pravi otrok ni prisoten, nastavite desnega otroka kot novo vozlišče

3. korak: Če ima vozlišče oba otroka, potem pop to iz čakalne vrste.

4. korak: Vnesite nove podatke v čakalno vrsto.

Ilustracija:

Razmislite o spodnjem nizu:

1. Prvi element bo koren (vrednost pri indeksu = 0 )

A je vzet kot koren

2. Naslednji element (pri indeksu = 1 ) bo levo in tretji element (index = 2 ) bo pravi otrok korena

B kot levi otrok in D kot desni otrok

3. četrti (indeks = 3 ) in peti element (indeks = 4 ) bo levi in ​​desni podrejeni vozlišča B

prednostna čakalna vrsta c++

E in F sta levi in ​​desni otrok B

4. Naslednji element (index = 5 ) bo levi podrejeni element vozlišča D

G je levi otrok vozlišča D

Tako se ustvari popolno binarno drevo.

Izvedba: Za izvedbo gradnje popolnega binarnega drevesa iz prečkanja vrstnega reda ravni je podano v ta objava .

Uporaba popolnega binarnega drevesa:

• Razvrščanje kopice
• Podatkovna struktura, ki temelji na razvrščanju kopice

Preverite, ali je dano binarno drevo popolno ali ne: Sledi ta objava da preveri, ali je dano binarno drevo popolno ali ne.