Logistična regresija je nadzorovan algoritem strojnega učenja uporablja za klasifikacijske naloge kjer je cilj napovedati verjetnost, da primerek pripada danemu razredu ali ne. Logistična regresija je statistični algoritem, ki analizira razmerje med dvema podatkovnima faktorjema. Članek raziskuje osnove logistične regresije, njene vrste in izvedbe.
Kazalo
- Kaj je logistična regresija?
- Logistična funkcija – sigmoidna funkcija
- Vrste logistične regresije
- Predpostavke logistične regresije
- Kako deluje logistična regresija?
- Implementacija kode za logistično regresijo
- Kompromis natančnosti priklica pri nastavitvi praga logistične regresije
- Kako oceniti model logistične regresije?
- Razlike med linearno in logistično regresijo
Kaj je logistična regresija?
Logistična regresija se uporablja za binarno razvrstitev kjer uporabljamo sigmoidno funkcijo , ki sprejme vhodne podatke kot neodvisne spremenljivke in ustvari vrednost verjetnosti med 0 in 1.
Na primer, imamo dva razreda, razred 0 in razred 1, če je vrednost logistične funkcije za vhod večja od 0,5 (vrednost praga), potem pripada razredu 1, sicer pa spada v razred 0. Imenuje se kot regresija, ker je razširitev linearna regresija vendar se uporablja predvsem za težave s klasifikacijo.
Ključne točke:
- Logistična regresija napove izhod kategorično odvisne spremenljivke. Zato mora biti rezultat kategorična ali diskretna vrednost.
- Lahko je bodisi Da ali Ne, 0 ali 1, True ali False itd., vendar namesto natančne vrednosti kot 0 in 1 podaja verjetnostne vrednosti, ki ležijo med 0 in 1.
- Pri logistični regresiji namesto regresijske črte prilagodimo logistično funkcijo v obliki črke S, ki napove dve največji vrednosti (0 ali 1).
Logistična funkcija – sigmoidna funkcija
- Sigmoidna funkcija je matematična funkcija, ki se uporablja za preslikavo predvidenih vrednosti v verjetnosti.
- Vsako realno vrednost preslika v drugo vrednost v območju od 0 do 1. Vrednost logistične regresije mora biti med 0 in 1, ki ne more preseči te meje, zato tvori krivuljo, kot je oblika S.
- Krivulja v obliki črke S se imenuje sigmoidna funkcija ali logistična funkcija.
- V logistični regresiji uporabljamo koncept mejne vrednosti, ki definira verjetnost 0 ali 1. Na primer, vrednosti nad mejno vrednostjo se nagibajo k 1, vrednosti pod mejnimi vrednostmi pa se nagibajo k 0.
Vrste logistične regresije
Na podlagi kategorij lahko logistično regresijo razvrstimo v tri vrste:
- Binom: V binomski logistični regresiji sta lahko samo dve možni vrsti odvisnih spremenljivk, kot sta 0 ali 1, uspešno ali neuspešno itd.
- Multinom: V multinomski logistični regresiji lahko obstajajo 3 ali več možnih neurejenih tipov odvisne spremenljivke, kot so mačka, psi ali ovce.
- Vrstni red: V ordinalni logistični regresiji so lahko 3 ali več možnih urejenih vrst odvisnih spremenljivk, kot so nizka, srednja ali visoka.
Predpostavke logistične regresije
Raziskali bomo predpostavke logistične regresije, saj je razumevanje teh predpostavk pomembno za zagotovitev, da uporabljamo ustrezno uporabo modela. Predpostavke vključujejo:
- Neodvisna opazovanja: Vsako opazovanje je neodvisno od drugega. kar pomeni, da med nobenimi vhodnimi spremenljivkami ni korelacije.
- Binarne odvisne spremenljivke: Predpostavlja se, da mora biti odvisna spremenljivka binarna ali dihotomna, kar pomeni, da lahko sprejme samo dve vrednosti. Za več kot dve kategoriji se uporabljajo funkcije SoftMax.
- Razmerje linearnosti med neodvisnimi spremenljivkami in logaritmom kvot: Razmerje med neodvisnimi spremenljivkami in logaritmom obetov odvisne spremenljivke mora biti linearno.
- Brez izstopajočih vrednosti: v naboru podatkov ne sme biti izstopajočih vrednosti.
- Velika velikost vzorca: Velikost vzorca je dovolj velika
Terminologije, vključene v logistično regresijo
Tukaj je nekaj pogostih izrazov, povezanih z logistično regresijo:
- Neodvisne spremenljivke: Vhodne značilnosti ali dejavniki napovedovanja, uporabljeni za napovedi odvisne spremenljivke.
- Odvisna spremenljivka: Ciljna spremenljivka v logističnem regresijskem modelu, ki jo poskušamo napovedati.
- Logistična funkcija: Formula, ki se uporablja za predstavitev, kako so neodvisne in odvisne spremenljivke povezane druga z drugo. Logistična funkcija pretvori vhodne spremenljivke v vrednost verjetnosti med 0 in 1, ki predstavlja verjetnost, da bo odvisna spremenljivka 1 ali 0.
- kvote: Je razmerje med nečim, kar se zgodi, in nečim, kar se ne zgodi. razlikuje se od verjetnosti, saj je verjetnost razmerje med tem, da se nekaj zgodi, in vsem, kar bi se lahko zgodilo.
- Log-kvote: Log-odds, znana tudi kot funkcija logit, je naravni logaritem kvot. Pri logistični regresiji so logaritemske verjetnosti odvisne spremenljivke modelirane kot linearna kombinacija neodvisnih spremenljivk in preseka.
- Koeficient: Ocenjeni parametri modela logistične regresije kažejo, kako so neodvisne in odvisne spremenljivke povezane druga z drugo.
- Prestrezanje: Stalni člen v modelu logistične regresije, ki predstavlja logaritem kvot, ko so vse neodvisne spremenljivke enake nič.
- Ocena največje verjetnosti : Metoda, uporabljena za oceno koeficientov modela logistične regresije, ki maksimira verjetnost opazovanja podatkov, podanih v modelu.
Kako deluje logistična regresija?
Logistični regresijski model transformira linearna regresija neprekinjen izhod vrednosti funkcije v izhod kategorične vrednosti z uporabo sigmoidne funkcije, ki preslika kateri koli nabor neodvisnih vhodnih spremenljivk z realnimi vrednostmi v vrednost med 0 in 1. Ta funkcija je znana kot logistična funkcija.
Naj bodo neodvisne vhodne funkcije:
in odvisna spremenljivka je Y, ki ima samo binarno vrednost, tj. 0 ali 1.
nato uporabite multilinearno funkcijo za vhodne spremenljivke X.
Tukaj
karkoli smo razpravljali zgoraj, je linearna regresija .
Sigmoidna funkcija
Zdaj uporabljamo sigmoidno funkcijo kjer bo vnos z in najdemo verjetnost med 0 in 1. torej predvideni y.
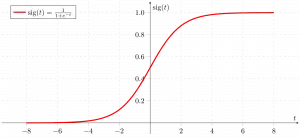
Sigmoidna funkcija
Kot je prikazano zgoraj, sigmoidna funkcija slike pretvori podatke zvezne spremenljivke v verjetnost torej med 0 in 1.
sigma(z) teži k 1 asz ightarrowinfty sigma(z) teži k 0 asz ightarrow-infty sigma(z) je vedno omejena med 0 in 1
kjer se verjetnost, da je razred, lahko meri kot:
java ubežni znaki
Enačba logistične regresije
Čudno je razmerje med tem, da se nekaj zgodi, in nečim, kar se ne zgodi. razlikuje se od verjetnosti, saj je verjetnost razmerje med tem, da se nekaj zgodi, in vsem, kar bi se lahko zgodilo. tako čudno bo:
Uporaba naravnega dnevnika na liho. potem bo log kvota:
potem bo končna enačba logistične regresije:
Funkcija verjetnosti za logistično regresijo
Predvidene verjetnosti bodo:
- za y=1 Predvidene verjetnosti bodo: p(X;b,w) = p(x)
- za y = 0 Predvidene verjetnosti bodo: 1-p(X;b,w) = 1-p(x)
Jemanje naravnih hlodov na obeh straneh
Gradient funkcije logaritma verjetnosti
Da bi našli ocene največje verjetnosti, razlikujemo glede na w,
Implementacija kode za logistično regresijo
Binomska logistična regresija:
Ciljna spremenljivka ima lahko samo 2 možni vrsti: 0 ali 1, ki lahko predstavljata zmago proti porazu, uspešno ali neuspešno, mrtvo ali živo itd., v tem primeru se uporabljajo sigmoidne funkcije, o katerih je že bilo govora zgoraj.
Uvažanje potrebnih knjižnic na podlagi zahteve modela. Ta koda Python prikazuje, kako uporabiti nabor podatkov o raku dojke za implementacijo modela logistične regresije za klasifikacijo.
Python3 # import the necessary libraries from sklearn.datasets import load_breast_cancer from sklearn.linear_model import LogisticRegression from sklearn.model_selection import train_test_split from sklearn.metrics import accuracy_score # load the breast cancer dataset X, y = load_breast_cancer(return_X_y=True) # split the train and test dataset X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.20, random_state=23) # LogisticRegression clf = LogisticRegression(random_state=0) clf.fit(X_train, y_train) # Prediction y_pred = clf.predict(X_test) acc = accuracy_score(y_test, y_pred) print('Logistic Regression model accuracy (in %):', acc*100)> Izhod :
Natančnost modela logistične regresije (v %): 95,6140350877193
Multinomska logistična regresija:
Ciljna spremenljivka ima lahko 3 ali več možnih vrst, ki niso urejene (tj. vrste nimajo kvantitativnega pomena), kot je bolezen A proti bolezni B proti bolezni C.
V tem primeru se funkcija softmax uporablja namesto sigmoidne funkcije. Funkcija Softmax za K razrede bo:
uporabo interneta
tukaj, K predstavlja število elementov v vektorju z, i, j pa ponovita vse elemente v vektorju.
Potem bo verjetnost za razred c:
V multinomski logistični regresiji ima lahko izhodna spremenljivka več kot dva možna diskretna izhoda . Razmislite o Digit Dataset.
Python3 from sklearn.model_selection import train_test_split from sklearn import datasets, linear_model, metrics # load the digit dataset digits = datasets.load_digits() # defining feature matrix(X) and response vector(y) X = digits.data y = digits.target # splitting X and y into training and testing sets X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.4, random_state=1) # create logistic regression object reg = linear_model.LogisticRegression() # train the model using the training sets reg.fit(X_train, y_train) # making predictions on the testing set y_pred = reg.predict(X_test) # comparing actual response values (y_test) # with predicted response values (y_pred) print('Logistic Regression model accuracy(in %):', metrics.accuracy_score(y_test, y_pred)*100)> Izhod:
Natančnost modela logistične regresije (v %): 96,52294853963839
Kako oceniti model logistične regresije?
Logistični regresijski model lahko ovrednotimo z uporabo naslednjih metrik:
- Natančnost: Natančnost zagotavlja delež pravilno razvrščenih primerkov.
Accuracy = frac{True , Positives + True , Negatives}{Total}
- Natančnost: Natančnost se osredotoča na točnost pozitivnih napovedi.
Precision = frac{True , Positives }{True, Positives + False , Positives}
- Priklic (občutljivost ali res pozitivna stopnja): Odpoklic meri delež pravilno napovedanih pozitivnih primerov med vsemi dejanskimi pozitivnimi primeri.
Recall = frac{ True , Positives}{True, Positives + False , Negatives}
- Rezultat F1: Rezultat F1 je harmonična sredina natančnosti in priklica.
F1 , Score = 2 * frac{Precision * Recall}{Precision + Recall}
- Območje pod krivuljo delovanja sprejemnika (AUC-ROC): Krivulja ROC prikazuje resnično pozitivno stopnjo proti lažno pozitivni stopnji pri različnih pragovih. AUC-ROC meri površino pod to krivuljo in zagotavlja agregatno merilo uspešnosti modela v različnih klasifikacijskih pragovih.
- Območje pod krivuljo natančnega priklica (AUC-PR): Podobno kot AUC-ROC, AUC-PR meri površino pod krivuljo natančnega priklica in zagotavlja povzetek delovanja modela v različnih kompromisih natančnega priklica.
Kompromis natančnosti priklica pri nastavitvi praga logistične regresije
Logistična regresija postane tehnika razvrščanja šele, ko se v sliko vnese odločilni prag. Nastavitev mejne vrednosti je zelo pomemben vidik logistične regresije in je odvisna od samega problema klasifikacije.
Na odločitev o vrednosti mejne vrednosti v veliki meri vplivajo vrednosti natančnost in odpoklic. V idealnem primeru želimo, da sta tako natančnost kot priklic 1, vendar je to redkokdaj.
V primeru a Kompromis Precision-Recall , za določitev praga uporabimo naslednje argumente:
- Nizka natančnost/visok priklic: V aplikacijah, kjer želimo zmanjšati število lažno negativnih rezultatov, ne da bi nujno zmanjšali število lažno pozitivnih rezultatov, izberemo vrednost odločitve, ki ima nizko vrednost Precision ali visoko vrednost Recall. Na primer, v aplikaciji za diagnozo raka ne želimo, da bi bil kateri koli prizadeti bolnik razvrščen kot neprizadet, ne da bi pri tem posvetili veliko pozornosti, če je bolniku napačno diagnosticiran rak. To je zato, ker je odsotnost raka mogoče ugotoviti z nadaljnjimi zdravstvenimi boleznimi, vendar prisotnosti bolezni ni mogoče ugotoviti pri že zavrnjenem kandidatu.
- Visoka natančnost/nizek priklic: V aplikacijah, kjer želimo zmanjšati število lažno pozitivnih rezultatov, ne da bi nujno zmanjšali število lažno negativnih rezultatov, izberemo vrednost odločitve, ki ima visoko vrednost Precision ali nizko vrednost Recall. Na primer, če razvrščamo stranke, ali se bodo na prilagojen oglas odzvale pozitivno ali negativno, želimo biti popolnoma prepričani, da se bo stranka na oglas odzvala pozitivno, saj lahko v nasprotnem primeru negativna reakcija povzroči izgubo potencialne prodaje zaradi stranka.
Razlike med linearno in logistično regresijo
Razlika med linearno regresijo in logistično regresijo je v tem, da je izhod linearne regresije zvezna vrednost, ki je lahko karkoli, medtem ko logistična regresija napove verjetnost, da primerek pripada danemu razredu ali ne.
Linearna regresija | Logistična regresija |
|---|---|
Linearna regresija se uporablja za napovedovanje zvezne odvisne spremenljivke z uporabo danega niza neodvisnih spremenljivk. | Logistična regresija se uporablja za napovedovanje kategorične odvisne spremenljivke z uporabo danega niza neodvisnih spremenljivk. |
Linearna regresija se uporablja za reševanje regresijskega problema. es5 proti es6 | Uporablja se za reševanje težav s klasifikacijo. |
Pri tem napovemo vrednost zveznih spremenljivk | Pri tem napovemo vrednosti kategoričnih spremenljivk |
V tem najdemo najboljšo linijo. | V tem najdemo S-krivuljo. |
Za oceno točnosti se uporablja metoda najmanjšega kvadrata. | Za oceno točnosti se uporablja metoda ocene največje verjetnosti. |
Rezultat mora biti stalna vrednost, kot je cena, starost itd. | Izhod mora biti kategorična vrednost, kot je 0 ali 1, Da ali ne itd. |
Zahteval je linearno razmerje med odvisnimi in neodvisnimi spremenljivkami. | Ni potrebno linearno razmerje. |
Med neodvisnimi spremenljivkami lahko obstaja kolinearnost. | Med neodvisnimi spremenljivkami ne sme biti kolinearnosti. |
Logistična regresija – pogosta vprašanja (FAQ)
Kaj je logistična regresija v strojnem učenju?
Logistična regresija je statistična metoda za razvoj modelov strojnega učenja z binarno odvisnimi spremenljivkami, tj. Logistična regresija je statistična tehnika, ki se uporablja za opisovanje podatkov in razmerja med eno odvisno spremenljivko in eno ali več neodvisnimi spremenljivkami.
Katere so tri vrste logistične regresije?
Logistična regresija je razvrščena v tri vrste: binarno, multinomsko in ordinalno. Razlikujejo se tako v izvedbi kot v teoriji. Binarna regresija se ukvarja z dvema možnima izidoma: da ali ne. Multinomska logistična regresija se uporablja, kadar obstajajo tri ali več vrednosti.
Zakaj se za problem klasifikacije uporablja logistična regresija?
Logistično regresijo je lažje izvajati, interpretirati in trenirati. Zelo hitro razvrsti neznane zapise. Ko je nabor podatkov linearno ločljiv, deluje dobro. Koeficiente modela je mogoče razlagati kot indikatorje pomembnosti lastnosti.
Kaj razlikuje logistično regresijo od linearne regresije?
Medtem ko se linearna regresija uporablja za napovedovanje neprekinjenih rezultatov, se logistična regresija uporablja za napovedovanje verjetnosti, da opazovanje sodi v določeno kategorijo. Logistična regresija uporablja logistično funkcijo v obliki črke S za preslikavo predvidenih vrednosti med 0 in 1.
Kakšno vlogo ima logistična funkcija v logistični regresiji?
Logistična regresija se opira na logistično funkcijo za pretvorbo izhoda v oceno verjetnosti. Ta rezultat predstavlja verjetnost, da opazovanje pripada določenemu razredu. Krivulja v obliki črke S pomaga pri določanju pragov in kategorizaciji podatkov v binarne rezultate.
