Podobni izrazi so členi v algebrskih izrazih, ki imajo enake spremenljivke, dvignjene na enake potence. Podobni in drugačni izrazi so vrste izrazov v algebri in lahko razlikujemo med podobnimi in drugačnimi izrazi tako, da preprosto preverimo spremenljivke in njihove moči. Algebraične člene definiramo kot posamezne člene, ki jih dobimo iz algebrske enačbe.
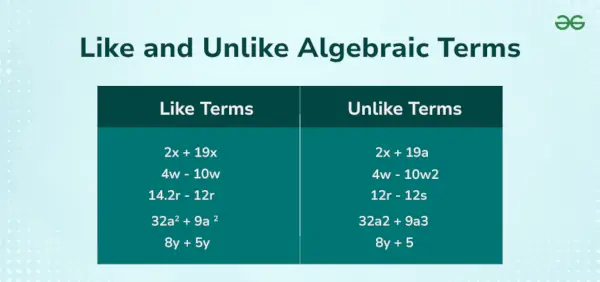
Na primer v algebraični enačbi 5x + 3 leta 2 = 12 imamo tri izraze, ki so, 5x, 3y², in 12 . tukaj, 5x, in 3 leta 2 so spremenljivi členi in 12 je stalni člen. Spodnja slika prikazuje podobne in drugačne izraze.
V tem članku se bomo podrobno seznanili s podobnimi izrazi, drugačnimi izrazi, njihovimi primeri, poenostavitvijo in drugimi.
Všeč mi Pogoji
Podobni izrazi so izrazi, ki imajo enake spremenljivke in je tudi moč vsake od spremenljivk enaka. Podobne izraze lahko kombiniramo, da poenostavimo algebraične izraze, in to je mogoče zelo enostavno izračunati. Na primer, 3y + 5y je algebraični izraz s podobnima členoma 3y in 5y. Da bi poenostavili ta algebraični izraz, dodamo podobne izraze. Tako je poenostavitev podanega izraza 8y.
Primeri pogojev za všečkanje
Podobni izrazi so izrazi, ki imajo enako spremenljivko s podobno močjo. Nekaj primerov podobnih izrazov je,
- 40xy 2 in 56xy 2 : V prvem primeru xy2je skupni koeficient za oba izraza. Torej so kot izrazi.
- 30z 2 in 18z 2 : z2je skupni koeficient za oba izraza. Torej so kot izrazi.
- 45abc in 29abc: abc je skupni koeficient za oba člena. Torej so kot izrazi.
- 18r 3 in 38r 3 : r3je skupni koeficient za oba izraza. Torej so kot izrazi.
- 2xy in 8xy: xy je skupni koeficient za oba izraza. Torej so kot izrazi.
Seštevanje in odštevanje podobnih izrazov
Enostavno lahko izvajamo seštevanje in odštevanje podobnih izrazov in ne potrebujemo nobenega posebnega pravila, na splošno so poenostavljeni z uporabo običajnih pravil seštevanja in odštevanja. Ta koncept lahko razumemo z naslednjim primerom.
Primer: Poenostavite 11x 3 + 5x 3
shraniti iz
rešitev:
Kot vidimo, so ti podobni izrazu, ker imajo podobne spremenljivke in njihova moč je prav tako konstantna.
Te izraze lahko enostavno dodamo neposredno.
= 11x3+ 5x3
= 16x3
To je mogoče, ker imata enake spremenljivke s podobno močjo in to lahko razumemo tako, da lahko neposredno seštejemo rupije k rupijam, tj. 5 Rs + 7 Rs je 12 Rs. Vendar ne moremo neposredno sešteti rupij z dolarji in 5 Rs + 7 dolarjev ni mogoče neposredno poenostaviti.
Podobno lahko tudi neposredno odštejemo podobne izraze, samo dodamo, dodamo podobne izraze, to lahko razumemo z naslednjim primerom.
Primer 1: Poenostavite 11x 3 – 5x 3
rešitev:
Kot vidimo, so ti podobni izrazu, ker imajo podobne spremenljivke in njihova moč je prav tako konstantna.
Te člene lahko enostavno neposredno odštejemo.
= 11x3– 5x3
seznam na Javi= 6x3
2. primer: dodajte 3 x + 2 in + 5 in 4 x − 3 in + 7.
rešitev:
(3 x + 2 in + 5) + (4 x − 3 in + 7)
= (3 x + 4x) +(2y + (-3y))+ (5 + 7)
= 7 x − in + 12
Za razliko od pogojev
Za razliko od izrazov so izrazi z različnimi spremenljivkami in vsaka od spremenljivk ima lahko različne eksponente ali pa tudi ne. Na primer, 9x + 6y je algebraični izraz z za razliko od izrazov. Ker ima dve različni spremenljivki x in y.
Če sta spremenljivki različni, ne preverjamo moči, saj sta na kakršen koli način drugačni od izrazov, če pa sta spremenljivki enaki, preverimo njihove moči, ker so lahko ali pa tudi ne podobni izrazom.
Kot na primer 5x2in 6x2so kot izrazi, ampak, 5x2in 6x3so drugačni izrazi.
Primeri nepodobnih izrazov
Za razliko od izrazov so izrazi, ki nimajo niti enakih spremenljivk niti podobne moči. Nekaj primerov drugačnih izrazov je,
- 40xy 2 in 56xy: Tukaj je v enem algebraičnem izrazu spremenljivka xy2in v drugem algebraičnem izrazu je spremenljivka xy. Obe spremenljivki sta enaki, vendar imata različne moči. Torej so drugačni izrazi.
- 45abc in 29ab: Tukaj je v enem algebrskem izrazu spremenljivka abc, v drugem algebrskem izrazu pa ab. Obe spremenljivki sta različni. Torej spadajo v kategorijo za razliko od izrazov.
Seštevanje in odštevanje različnih členov
Seštevanje in odštevanje se ne izvaja med, za razliko od členov, tj. ne moremo seštevati ali odštevati za razliko od členov in to lahko razumemo na primeru, ko 6 kg riža ne moremo dodati 5 litrov mleka. Na enak način ne moremo seštevati ali odštevati, za razliko od izrazov.
Na primer, 3xy + 5x ni mogoče nadalje rešiti in ostane na enak način.
Razlika med podobnimi in drugačnimi izrazi
Razlike med podobnimi in drugačnimi izrazi so obravnavane v spodnji tabeli.
| Funkcija | Všeč mi Pogoji | Za razliko od pogojev |
|---|---|---|
| Opredelitev | Podobni izrazi so izrazi, ki imajo enake spremenljivke in enake vrednosti eksponentov. | Za razliko od izrazov so izrazi, ki imajo različne spremenljivke in eksponenti. |
| Poenostavitev java util datum | Podobne izraze lahko enostavno poenostavimo. | Za razliko od izrazov, ki jih ni mogoče poenostaviti. |
| Združevanje izrazov | Podobne pogoje je mogoče združiti neposredno za izračun. | Za razliko od izrazov ni mogoče neposredno kombinirati, ker predstavljajo različne količine |
| Seštevanje ali odštevanje | Seštevanje in odštevanje je mogoče doseči v podobnih izrazih. | Za razliko od izrazov ne moremo seštevati ali odštevati. |
| Primeri | Primeri podobnih izrazov so x2, 5x2, -11/3x2itd. | Primeri izrazov za razliko so x2in 5x3, -11/3x itd. |
Preberi več
- Algebraični izrazi
- Vrste algebrskih izrazov
Primeri za podobne in drugačne algebraične izraze
Primer 1: Prepoznajte podobne in drugačne izraze iz: 3x, 5xy, 18x 2 in 5x 3 , 29xy, 50x 3
rešitev:
Podobni in različni izrazi iz danih izrazov so,
Pogoji všečkanja: (5xy, 29xy) in (5x3, 50x3)
Za razliko od pogojev: 3x, 18x2in
if else zanka v Javi
Primer 2: Poenostavite 3xy + 5x 2 + 11ab – 4xy
rešitev:
Podan izraz: 3xy + 5x2+ 11ab – 4xy
Podoben izraz v danem izrazu, 3xy in -4xy
Pri poenostavitvi,
= 3xy – 4xy + 5x2+ 11ab
= -xy + 5x2+ 11ab
Ostali so vsi členi drugačni členi, zato jih ni mogoče nadalje reševati.
Primer 3: Poenostavite 8x + 15x 2 + 11x – 4x 2
rešitev:
Podan izraz: 8x + 15x2+ 11x – 4x2
Podoben izraz v danem izrazu, (8x, 11x) in (15x2, -4x2)
Pri poenostavitvi,
= 8x + 11x + 15x2– 4x2
= 19x – 11x2
Ostali so vsi členi drugačni členi, zato jih ni mogoče nadalje reševati.
Algebraični izrazi so všeč in drugačni – pogosta vprašanja
Kaj so algebraični izrazi?
Algebraični členi so posamezni členi, dobljeni iz algebrske enačbe, tj. členi, deljeni s simboli operacij, kot sta + in -.
Kaj so podobni in drugačni izrazi?
Podobni in različni členi so členi algebraičnega izraza. V podobnih imamo podobne spremenljivke in je moč eksponenta enaka, medtem ko so v nasprotnih izrazih spremenljivke in njihova moč različni.
zamenjaj niz v Javi
Kakšna je razlika med podobnimi in drugačnimi algebrskimi izrazi?
Osnovna razlika med podobnimi in drugačnimi izrazi je v tem, da imamo v podobnem izrazu isto spremenljivko z enakimi močmi, medtem ko imamo v nasprotju z izrazi različne spremenljivke z različnimi močmi.
Kako najti podobne in drugačne algebraične izraze?
Podobni izrazi so izrazi, ki imajo enake spremenljivke z enakimi potencami, različni izrazi pa so izrazi z različnimi spremenljivkami in različnimi potencami, ki jih zlahka prepoznamo že s pregledovanjem spremenljivk.
Ali lahko seštevamo ali odštevamo kot algebraične člene?
Z lahkoto lahko seštevamo ali odštevamo podobne člene, kot sta 5x in 11x, so podobni členi in jih je mogoče sešteti kot 16x.
Ali lahko seštevamo ali odštevamo za razliko od algebrskih izrazov?
Za razliko od izrazov, kot sta 2x in 3y, ne moremo seštevati ali odštevati. Tako za razliko od izrazov ni mogoče seštevati ali odštevati.
