Središče trikotnika je presečišče vseh treh simetral kotov trikotnika. Središče je pomembna točka v trikotniku, kjer se črte, ki razpolovijo kote, združijo. Ta točka je tudi središče kroga, imenovanega Vpisani krog, ki se popolnoma prilega notranjosti trikotnika in se enako dotika vseh treh strani. Ta članek pokriva različne koncepte središča trikotnika, na primer zakaj je ta točka pomembna, kako jo najti s šestilom ali številkami in lastnosti središča kroga.

Kazalo

• Kaj je središče trikotnika?
• Lastnosti središča trikotnika
• Formula središča trikotnika
• Kako najti središče trikotnika
• Centroid, Circumcenter, Incenter, Orthocenter

Kaj je središče trikotnika?

Središče trikotnika je, kot že ime pove, središče trikotnika. Ta točka, ki ji pravimo središče, nastane na stičišču, kjer se srečajo vse črte, ki razpolovijo notranje kote. Oddaljenost točke od vseh treh strani trikotnika je enaka. Vpisani krog trikotnika se prilega tudi popolnemu krogu znotraj trikotnika in ta krog se imenuje vpisani krog trikotnika.

Opredelitev središča

Središče trikotnika je točka znotraj trikotnika, kjer se združijo vse tri črte, ki razpolovijo njegove notranje kote. Ta točka je enako oddaljena od treh strani trikotnika, zaradi česar je kot sredina trikotnika. Je tudi središče največjega kroga, ki se lahko tesno prilega notranjosti trikotnika, ki ga imenujemo vpisani krog. Za simboliziranje središča običajno uporabljamo črko I,

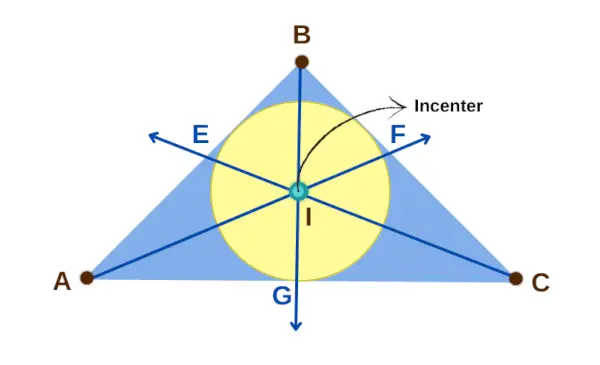
Središče trikotnika

Lastnosti središča trikotnika

Nekatere pomembne lastnosti središča trikotnika so navedene spodaj:

Lastnost 1: če jaz je središče trikotnika ABC, potem so trije pari daljic enako dolgi: AE in AG, CG in CF ter BF in BE. To pomeni, da je AE = AG, CG = CF in BF = BE.

Lastnost 2: Središče jaz ima tudi poseben odnos s koti trikotnika. To povzroči, da sta kota ∠BAI in ∠CAI enaka, ∠BCI in ∠ACI enaka ter ∠ABI in ∠CBI enaka. To sledi izreku simetrale kota.

Lastnost 3: Središče jaz je središče kroga, ki se dotika vseh treh strani trikotnika, in razdalje od jaz do stranic trikotnika (EI, FI, GI) so vse enake. Te razdalje se imenujejo inradiji ali polmeri vpisanega kroga.

Lastnost 4: Ploščino trikotnika lahko izračunate s polperimetrom (s) in inradijem (r). Formula je A = sr, kjer je A ploščina, s je polobod (s = (a + b + c)/2, kjer so a, b in c dolžine stranic trikotnika), r pa je inradius.

Lastnost 5: Središče trikotnika vedno ostane znotraj trikotnika. Za razliko od ortocentra, ki je lahko v nekaterih primerih zunaj trikotnika, je središče vpisa vedno v mejah trikotnika.

Formula središča trikotnika

Formula za iskanje vpisanega središča formule s 3 koordinatami (x₁, in₁), (x₂, in₂) in (x₃, in₃) je:

{(ax ₁ + bx ₂ + cx ₃ )/(a + b + c), (je ₁ + od ₂ + c ₃ )/(a + b + c)}

Preprosto povedano, če želite dobiti središče, morate:

• Pomnožite x-koordinato točke A z dolžino stranice a, x-koordinato točke B z dolžino stranice b in koordinato x točke C z dolžino stranice c. Nato jih seštejte skupaj.
• Rezultat delite z vsoto dolžin stranic a, b in c.
• Isti postopek ponovite za koordinate y, vendar z uporabo dolžin stranic a, b in c.

Formula kota središča trikotnika

Formula za iskanje središča kota trikotnika je naslednja:

Naj bodo v trikotniku D, F in G točke, kjer simetrale kotov kotov A, B in C sekajo stranice BC, AC in AB.

Kot ∠AIB (kjer je I središče trikotnika) lahko izračunate po formuli:

∠AIB = 180° – (polovica vsote kotov A in B)

ALI

∠AIB = 180° – (∠A + ∠B)/2

Kako najti središče trikotnika

Obstajata dva načina za iskanje središča trikotnika. Pri gradnji lociramo središče vpisa tako, da narišemo simetrale kotov trikotnika. V koordinatni geometriji uporabljamo formulo za določitev središča vpisa.

Uporaba koordinatne geometrije : Poiščite središče vpisanega trikotnika s koordinatami, podanimi kot: A(2, 2), B(6, 2) in C(4, 5)

Po podanih informacijah

• (x₁, in₁) = (2, 2)
• (x₂, in₂) = (6, 2)
• (x₃, in₃) = (4, 5)

Vemo, da je središče trikotnika:

I(x, y) = {(ax ₁ + bx ₂ + cx ₃ )/(a + b + c), (je ₁ + od ₂ + c ₃ )/(a + b + c)}

Za stran a: Razdalja med točkama B in C = √((6 – 4)²+ (2 – 5)²) = √8

Za stran b: Razdalja med točkama A in C = √((2 – 4)²+ (2 – 5)²) = √13

Za stran c: razdalja med točkama A in B = √((6 – 2)²+ (2 – 2)²) = 4

Če vnesemo vrednosti a, b, c v formulo vpisanega središča, dobimo:

I(x, y) = {(8×2 + 13×5 + 4×4)/(8 + 13 +4), (8×2 + 13×2 + 4×5)/(8 + 13 +4) )}

⇒ I(x, y) = (16 + 78 + 16)/(25), (16 + 26 + 20)/(25)

⇒ I(x, y) = (110/25, 62/25) = (22/5,62/25)

∴ Središče vpisanega trikotnika ABC s koordinatami je (22/5,62/25)

Kako sestaviti središče trikotnika?

Če želite zgraditi središče trikotnika, boste morali uporabiti šestilo. Pri uporabi kompasa sledite spodnjim korakom:

Korak 1: En konec šestila položite na vrh trikotnika, drugi konec pa se dotika ene stranice.

2. korak: S šestilom narišite dva loka na obeh straneh trikotnika.

3. korak: Z enako razdaljo na šestilu naredite dva loka znotraj trikotnika. Ti loki se morajo križati od tam, kjer se dotikajo stranic.

4. korak: Narišite črto od vrha trikotnika do mesta, kjer se križata notranja loka.

5. korak: Ponovite iste korake od drugega vrha trikotnika.

6. korak: Tam, kjer se črti srečata ali križata, je središče trikotnika.

Središče pravokotnega trikotnika

Središče če a Pravokotni trikotnik je točka, kjer se stikata vse simetrale kotov pravokotnega trikotnika. Če strani pravokotnega trikotnika merijo a, b in c, potem je polmer vpisanega kroga 'r' podan kot r = (ab)/(a + b + c). Središče pravokotnega trikotnika je prikazano spodaj:

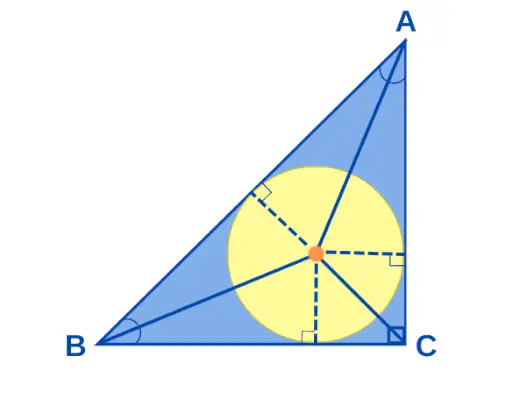
Središče pravokotnega trikotnika

Centroid, Circumcenter, Incenter, Orthocenter

Centroid, Circumcenter, Incenter in Orthocenter so štiri pomembne točke, povezane s traingle. Primerjava med Centroid, Circumcenter, Incenter in Orthocenter je prikazana spodaj:

Prav tako preverite

• Območje trikotnika
• Obseg trikotnika
• Lastnost vsote kotov trikotnika

Primeri središča trikotnika

Primer 1: Izračunaj središče vpisa trikotnika ABC. AB= 8 cm, BC= 15 cm, CA= 17 cm.

rešitev:

Uporaba formule središča trikotnika = (aA + bB + cC)/(a + b + c)

kje,

• a = 8
• b = 15
• c = 17

In koti so,

• A = 30°
• B = 60°
• C = 90°

Če te vrednosti vnesemo v formulo, da dobimo,

⇒ {(8)(30) + (15)(60) + (17)(90)}/{8 + 15 + 17}

⇒ (240 + 900 + 1530)/40

⇒ 2670/40

⇒ 66,75

Primer 2: Jane je izračunala površino trikotnega polja kot 120 kvadratnih metrov. Obseg igrišča je 36 metrov. Če je znotraj trikotnika narisan krog tako, da se dotika vseh stranic trikotnika, pomagaj Jane izračunati polmer trikotnika.

rešitev:

Po podanih informacijah je

Površina trikotnika = 120 kvadratnih metrov

Obseg trikotnika = 36 metrov

Vemo, da je ploščina trikotnika = r × s

s = polobod

nadnapis v ilustratorju

s = p/2 = 36/2 = 18

A = r × s

r = A/s

r = 120/18

r = 6,67 metra

Vadbene naloge o središčnici trikotnika

Problem 1: Dan je trikotnik PQR z oglišči P(1, 2), Q(4, 6) in R(7, 2), poiščite koordinate središča vpisanega.

2. naloga: Sestavite trikotnik ABC z ∠A = 45°, ∠B = 60° in ∠C = 75°. Uporabite metodo konstrukcije, da poiščete središče.

3. naloga: V trikotniku LMN, če je ∠L = 75°, ∠M = 60° in ∠N = 45°, poiščite koordinate vpisanega središča.

4. naloga: Sestavite trikotnik XYZ z ∠X = 80°, ∠Y = 50° in ∠Z = 50°. Uporabite metodo konstrukcije, da poiščete središče.

Središče trikotnika: pogosta vprašanja

Kaj je središče trikotnika?

Središče trikotnika je točka, kjer se sekata simetrali notranjih kotov. Je enako oddaljen od vseh treh strani trikotnika.

Kakšen je pomen središča v trikotniku?

Središče vpisa je pomembno, saj je središče vpisanega kroga trikotnika, največjega kroga, ki se prilega notranjosti trikotnika. Ima lastnost, da je z vseh strani enako oddaljena.

Ali je lahko središče izven trikotnika?

Ne, središče je vedno znotraj trikotnika. To je sočasnost simetral kotov in po definiciji mora biti znotraj meja trikotnika.

Kako je središče izdelano s šestilom in ravnilom?

Če želite sestaviti središče, s šestilom narišite simetrale kotov iz vsakega oglišča na nasprotno stran. Središče je točka, kjer se simetrali sekata.

Kaj je Incenter Formula?

Formulo za središče trikotnika lahko zapišemo kot:

frac{(aA+bB+cC)}{a+b+c}

Kakšne so lastnosti središča trikotnika?

Incenter ima nekaj ključnih lastnosti. Je enako oddaljen od stranic trikotnika, kar pomeni, da sta razdalji do stranic enaki. Prav tako je presečišče simetral kotov, ki deli kote na dva enaka dela.

Kako se določi Incentre?

Če želite določiti središče vpisa, morate najti, kje se simetrali kotov sekata. To lahko storite s formulo vpisa ali tako, da narišete simetrale kotov in poiščete njihovo presečišče.

Kakšna je razlika med Incentre in Circumcentre?

Glavna razlika med središčem na sredini in središčem, ki ga obkroža, je njihov fokus. Središče vpisanega kota se nanaša na simetrale kota in je središče včrtanega kroga, medtem ko se središče opisanega kroga nanaša na simetrale pravokotnic in je središče opisanega kroga.

Ali sta Incentre in Centroid enaka?

Ne, središče in centroid sta različna. Središče je tam, kjer se sekata simetrala kota, medtem ko je težišče tam, kjer se sekata mediani. Mediane povezujejo oglišča s središčem nasprotne stranice.

Ali je Incentre in Orthocentre isto?

Ne, središče in ortocenter nista isto. Središče je točka, kjer se kota razpolavljata, medtem ko ortocenter vključuje višine – črte iz vsakega oglišča, pravokotne na nasprotno stran. So različne točke v trikotniku.