- DFA se nanaša na deterministične končne avtomate. Deterministično se nanaša na edinstvenost izračuna. Končni avtomati se imenujejo deterministični končni avtomati, če stroj bere vhodni niz en simbol naenkrat.
- V DFA obstaja samo ena pot za določen vnos iz trenutnega stanja v naslednje stanje.
- DFA ne sprejme ničelnega premika, kar pomeni, da DFA ne more spremeniti stanja brez vnosnega znaka.
- DFA lahko vsebuje več končnih stanj. Uporablja se v leksikalni analizi v prevajalniku.
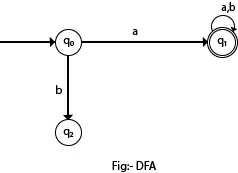
V naslednjem diagramu lahko vidimo, da od stanja q0 za vhod a obstaja samo ena pot, ki vodi do q1. Podobno je od q0 samo ena pot za vhod b do q2.
Formalna definicija DFA
DFA je zbirka 5-tork, kot smo opisali v definiciji FA.
Q: finite set of states ∑: finite set of the input symbol q0: initial state F: final state δ: Transition function
Prehodno funkcijo lahko definiramo kot:
δ: Q x ∑→Q
Grafična predstavitev DFA
DFA je mogoče predstaviti z digrafi, imenovanimi diagrami stanja. V katerem:
- Stanje je predstavljeno z vozlišči.
- Lok, označen z vhodnim znakom, prikazuje prehode.
- Začetno stanje je označeno s puščico.
- Končno stanje je označeno z dvojnim krogom.
Primer 1:
Q = {q0, q1, q2} ∑ = {0, 1} q0 = {q0} F = {q2} rešitev:
Diagram prehoda:

Prehodna tabela:
| Sedanje stanje | Naslednje stanje za vnos 0 | Naslednje stanje vnosa 1 |
|---|---|---|
| →q0 | q0 | q1 |
| q1 | q2 | q1 |
| *q2 | q2 | q2 |
Primer 2:
DFA z ∑ = {0, 1} sprejme vse, ki se začnejo z 0.
rešitev:

Pojasnilo:
- V zgornjem diagramu lahko vidimo, da pri danem 0 kot vhodu v DFA v stanju q0 DFA spremeni stanje v q1 in vedno preide v končno stanje q1 ob začetnem vnosu 0. Sprejme lahko 00, 01, 000, 001 ... .itd. Ne more sprejeti nobenega niza, ki se začne z 1, ker nikoli ne bo šel v končno stanje na nizu, ki se začne z 1.
Primer 3:
DFA z ∑ = {0, 1} sprejme vse, ki se končajo z 0.
rešitev:

Pojasnilo:
V zgornjem diagramu lahko vidimo, da pri danem 0 kot vhodu v DFA v stanju q0 DFA spremeni stanje v q1. Sprejme lahko kateri koli niz, ki se konča z 0, na primer 00, 10, 110, 100 ... itd. Ne more sprejeti nobenega niza, ki se konča z 1, ker nikoli ne bo šel v končno stanje q1 na vhodu 1, tako da niz, ki se konča z 1, ne bo sprejet ali bo zavrnjen.
