Težave z regresijo in verjetnostno klasifikacijo je mogoče rešiti z uporabo Gaussovega procesa (GP), tehnike nadzorovanega učenja. Ker lahko vsak Gaussov proces razumemo kot neskončnodimenzionalno posplošitev večvariant Gaussove porazdelitve , se v imenu pojavlja izraz Gaussian. V tej objavi bomo razpravljali o Gaussovih procesih za regresijo, ki se imenujejo tudi regresija Gaussovega procesa (GPR). Številna resnična vprašanja na področjih znanosti o materialih, kemije, fizike in biologije so bila rešena z uporabo GPR.
Kazalo
- Regresija Gaussovega procesa (GPR)
- Ključni koncepti regresije Gaussovega procesa (GPR)
- Matematični koncept regresije Gaussovega procesa (GPR)
- Implementacija Gaussovega procesa v Pythonu
Regresija Gaussovega procesa (GPR)
Gaussova procesna regresija (GPR) je močna in prilagodljiva neparametrična regresijska tehnika, ki se uporablja v strojno učenje in statistika . Še posebej je uporabno pri obravnavanju problemov, ki vključujejo neprekinjene podatke, kjer razmerje med vhodnimi spremenljivkami in izhodom ni eksplicitno znano ali je lahko zapleteno. GPR je Bayesov pristop, ki lahko modelira gotovost v napovedih, zaradi česar je dragoceno orodje za različne aplikacije, vključno z optimizacijo, napovedovanjem časovnih vrst in še več. GPR temelji na konceptu Gaussovega procesa, ki je zbirka naključnih spremenljivk, katerih vsako končno število ima skupno Gaussovo porazdelitev. Gaussov proces si lahko predstavljamo kot porazdelitev funkcij.
Ključni koncepti regresije Gaussovega procesa (GPR)
Gaussainov proces
Neparametrični, verjetnostni model, imenovan a Gaussov proces (GP) se uporablja v statistiki in strojnem učenju za regresijo, klasifikacijo in kvantifikacijo negotovosti. Prikazuje skupino naključnih spremenljivk, od katerih ima vsaka skupno Gaussovo porazdelitev in ima lahko končno število. GP so vsestranska in učinkovita tehnika za modeliranje zapletenih odnosov v podatkih in izdelavo napovedi s povezano negotovostjo.
Značilnosti Gaussovih procesov :
pretvorba int v niz
- Neparametrična narava : zdravniki splošne medicine se lahko prilagodijo kompleksnosti podatkov, ker se ne zanašajo na določeno število parametrov modela
- Probabilistične napovedi : Napovedi splošnih zdravnikov je mogoče kvantificirati, ker podajajo napovedi kot porazdelitve verjetnosti.
- Interpolacija in glajenje : GP so uporabni za šumne ali nepravilno vzorčene podatke, ker so dobri pri glajenju šumnih podatkov in interpolaciji med podatkovnimi točkami.
- Marginalizacija hiperparametrov : Z odpravo zahteve po eksplicitnem prilagajanju hiperparametrov marginalizirajo hiperparametre, zaradi česar je model enostavnejši.
Srednja funkcija
Predvidena vrednost funkcije, ki se modelira na vsaki vhodni točki, je predstavljena z srednja funkcija v Gaussovih procesih (GP). Deluje kot temeljna predpostavka glede osnovne podatkovne strukture. Funkcija povprečja je pogosto privzeto nastavljena na nič, ni nujno, in jo je mogoče spremeniti glede na lastnosti podatkov ali strokovno znanje o domeni. Z vplivanjem na osrednjo tendenco napovedi pomaga splošnim zdravnikom pri prepoznavanju vzorcev ali trendov v podatkih. Zdravniki splošne medicine zagotavljajo verjetnostne napovedi, ki vsebujejo negotovost, kot tudi točkovne ocene z vključitvijo srednje funkcije
Kovariančna (jedrna) funkcija
The kovariančna funkcija , imenovana tudi funkcija jedra, meri, kako podobne so si vhodne podatkovne točke v Gaussovih procesih (GP). Bistvenega pomena je pri karakterizaciji obnašanja modela GP, ki vpliva na izbiro funkcij iz prejšnje porazdelitve. Kovariančna funkcija meri podobnosti po parih, da ugotovi korelacijo med vrednostmi funkcije. GP se lahko prilagodijo širokemu naboru podatkovnih vzorcev, od gladkih trendov do kompleksnih struktur, ker različne funkcije jedra zajamejo različne vrste korelacije. Na delovanje modela lahko močno vpliva izbira jedra.
Predhodne distribucije
The predhodna distribucija , v Gaussovih procesih (GP), je naše razumevanje funkcij pred opazovanjem kakršnih koli podatkov. Običajno je opisana s kovariančno (jedrno) funkcijo in srednjo funkcijo. Medtem ko kovariančna funkcija opisuje podobnost ali korelacijo med vrednostmi funkcije na različnih vhodnih točkah, povprečna funkcija kodira naša prejšnja pričakovanja. Splošni zdravniki to predhodno uporabijo za ustvarjanje porazdelitve po funkcijah. V GP je mogoče izbrati predhodne vrednosti, ki predstavljajo negotovost podatkov, integrirajo znanje domene ali označujejo gladkost.
Posteriorne porazdelitve
Gaussovi procesi kasnejša distribucija prikazuje naše revidirane predpostavke o funkcijah po opazovanju podatkov. Združuje verjetnost podatkov glede na funkcijo in prejšnjo porazdelitev. Posterior v regresiji GP ponuja porazdelitev po funkcijah, ki se najbolj ujemajo z opazovanimi podatki. Z omogočanjem verjetnostnih napovedi in kvantifikacijo negotovosti posteriorna porazdelitev odraža kompromis med predhodnimi prepričanji, shranjenimi v predhodni porazdelitvi, in informacijami, ki jih zagotavljajo podatki.
Matematični koncept regresije Gaussovega procesa (GPR)
Za regresijske naloge se uporablja neparametrični, verjetnostni model strojnega učenja, imenovan regresija Gaussovega procesa (GP). Pri modeliranju zapletenih in dvoumnih interakcij med vhodnimi in izhodnimi spremenljivkami je to močno orodje. Predpostavlja se, da multivariatna Gaussova porazdelitev ustvari podatkovne točke v regresiji GP, cilj pa je sklepati o tej porazdelitvi.
Regresijski model GP ima naslednji matematični izraz. Predpostavimo x1, x2,…..,xnso vhodne podatkovne točke, kjer x pripadajo realnim številom (-2,-1,0,1…), (xjaz
Predpostavimo y1, in2 ,……., innso izhodne vrednosti, kjer je yjazpripada realnemu številu (yjaz
Regresijski model GP predpostavlja, da Gaussov proces s srednjo funkcijo (
Nato je na nizu testnih lokacij x* porazdelitev f podana z:
Običajno se jedrne funkcije uporabljajo za definiranje srednje funkcije in kovariančne funkcije. Kot ponazoritev je kvadratno eksponentno jedro, ki se pogosto uporablja, opisano kot:
Kje,
k(x_{i}, x_{j}) = Funkcija jedra je predstavljena s tem in izračuna korelacijo ali podobnost med dvema vhodnima podatkovnima točkama, xjazin xj.sigma^2 = Parameter variance jedra je to. Vzpostavi lestvico ali navpično širjenje funkcije jedra. Ureja, kako močno so podatkovne točke povezane. Višjisigma^2 daje jedrno funkcijo z večjo varianco.- exp: Eksponentna funkcija je odgovorna za povišanje e na potenco argumenta.
||x_{i} – x_{j}||^2 : Razlika med vhodnimi podatkovnimi točkami, xjazin xj, je kvadrat evklidske razdalje. Izmeri se geometrijska razdalja med točkami v prostoru značilnosti.- l2: To je predstavitev lestvice dolžine ali značilne dolžine jedra. Uravnava hitrost, s katero se poslabša funkcija jedra, ko so podatkovne točke bolj oddaljene. Nižji l povzroči hitrejšo degradacijo jedra.
Regresijski model GP uporablja Bayesovo sklepanje za določitev porazdelitve f, ki je najverjetneje ustvarila podatke glede na niz podatkov o usposabljanju (x, y). Da bi to naredili, je treba izračunati posteriorno porazdelitev f glede na podatke, ki je definirana na naslednji način:
če po povzetku Rudyarda Kiplinga
kjer je mejna verjetnost podatkov p(y|x), je predhodna porazdelitev f p(f) in verjetnost podatkov glede na funkcijo f (y|x,f).
Ko se nauči posteriorne porazdelitve f, model izračuna posteriorno napovedno porazdelitev, da naredi napovedi na dodatnih testnih točkah x*. Opredelimo ga lahko na naslednji način:
Kje,
p(f^*|x*, y, x) = To kaže glede na podatke o usposabljanju y in x pogojno verjetnost predvidenih vrednosti funkcije f*na novi vhodni točki x*Povedano drugače, to je verjetnostna porazdelitev vseh potencialnih funkcijskih vrednosti na novem vhodnem mestu x*, odvisno od opazovanih podatkov y in njihovih ujemajočih se vhodnih lokacij x.int p(f^*|x^*, f)p(f|y,x)df = V tem delu enačbe je za določitev pogojne verjetnosti uporabljen integral. Integral zajema vse potencialne vrednosti funkcije f.p(f^*|x^*, f) = To je pogojna verjetnostna porazdelitev pričakovanih vrednosti funkcije f*pri x*, glede na vrednosti funkcije f na nekaterih vmesnih lokacijah.p(f|y,x) = Glede na opazovane podatke (y) in njihove vhodne lokacije (x) je to pogojna verjetnostna porazdelitev vrednosti funkcije (f).
Za naloge, kot sta odločanje ob upoštevanju negotovosti in aktivno učenje, ta porazdelitev ponuja merilo negotovosti napovedi, kar je lahko koristno.
Koraki v regresiji Gaussovega procesa
- Zbiranje podatkov : Zberite vhodno-izhodne podatkovne pare za vaš problem regresije.
- Izberite funkcijo jedra : Izberite ustrezno kovariančno funkcijo (jedro), ki ustreza vaši težavi. Izbira jedra vpliva na obliko funkcij, ki jih GPR lahko modelira.
- Optimizacija parametrov : Ocenite hiperparametre jedrne funkcije z maksimiranjem verjetnosti podatkov. To je mogoče storiti z optimizacijskimi tehnikami, kot je gradientni spust.
- Napoved: Glede na nov vnos uporabite usposobljeni model GPR za napovedi. GPR zagotavlja tako predvideno povprečje kot povezano negotovost (varianco).
Implementacija regresije Gaussovega procesa (GPR)
Python import numpy as np import matplotlib.pyplot as plt from sklearn.gaussian_process import GaussianProcessRegressor from sklearn.gaussian_process.kernels import RBF from sklearn.model_selection import train_test_split # Generate sample data np.random.seed(0) X = np.sort(5 * np.random.rand(80, 1), axis=0) y = np.sin(X).ravel() # Add noise to the data y += 0.1 * np.random.randn(80) # Define the kernel (RBF kernel) kernel = 1.0 * RBF(length_scale=1.0) # Create a Gaussian Process Regressor with the defined kernel gp = GaussianProcessRegressor(kernel=kernel, n_restarts_optimizer=10) # Split the data into training and testing sets X_train, X_test, y_train, y_test = train_test_split( X, y, test_size=0.5, random_state=0) # Fit the Gaussian Process model to the training data gp.fit(X_train, y_train) # Make predictions on the test data y_pred, sigma = gp.predict(X_test, return_std=True) # Visualize the results x = np.linspace(0, 5, 1000)[:, np.newaxis] y_mean, y_cov = gp.predict(x, return_cov=True) plt.figure(figsize=(10, 5)) plt.scatter(X_train, y_train, c='r', label='Training Data') plt.plot(x, y_mean, 'k', lw=2, zorder=9, label='Predicted Mean') plt.fill_between(x[:, 0], y_mean - 1.96 * np.sqrt(np.diag(y_cov)), y_mean + 1.96 * np.sqrt(np.diag(y_cov)), alpha=0.2, color='k', label='95% Confidence Interval') plt.xlabel('X') plt.ylabel('y') plt.legend() plt.show()> Izhod:
V tej kodi najprej ustvarite nekaj vzorčnih podatkovnih točk z dodanim šumom, nato definirajte jedro RBF in ustvarite a Gaussov procesni regresor z njim. Model se uri na podlagi podatkov o usposabljanju in se uporablja za izdelavo napovedi na podlagi testnih podatkov. Na koncu so rezultati prikazani z grafom, ki prikazuje podatke o vadbi, predvideno povprečje in 95-odstotni interval zaupanja.
Implementacija Gaussovega procesa v Pythonu
Scikit Naučite se
Python import matplotlib.pyplot as plt import numpy as np from scipy import linalg from sklearn.gaussian_process import kernels,GaussianProcessRegressor ## check version import sys import sklearn print(sys.version) !python --version print("numpy:", np.__version__) print("sklearn:",sklearn.__version__)> Potrebne knjižnice za Gaussovo procesno regresijo (GPR) v Python so uvožene s to kodo; to so SciPy za funkcije linearne algebre, NumPy za numerične operacije in Matplotlib za vizualizacijo podatkov. Da se prepriča o združljivosti s potrebnimi paketi, dodatno preveri različico Pythona in jo natisne skupaj z različicama NumPy in scikit-learn (sklearn).
Izbira jedra
Python np.random.seed(0) n=50 kernel_ =[kernels.RBF (), kernels.RationalQuadratic(), kernels.ExpSineSquared(periodicity=10.0), kernels.DotProduct(sigma_0=1.0)**2, kernels.Matern() ] print(kernel_, '
')> Izhod:
c++ razdeli niz
[RBF(length_scale=1),
RationalQuadratic(alpha=1, length_scale=1),
ExpSineSquared(length_scale=1, periodičnost=10),
DotProduct(sigma_0=1) ** 2,
Mater(length_scale=1, nu=1,5)]
Koda podaja število testnih mest (n) in inicializira a naključno seme . Za prikaz izbranih jeder ustvari seznam več funkcij jedra in natisne seznam.
Primerjava in vizualizacija jedra
Python for kernel in kernel_: # Gaussian process gp = GaussianProcessRegressor(kernel=kernel) # Prior x_test = np.linspace(-5, 5, n).reshape(-1, 1) mu_prior, sd_prior = gp.predict(x_test, return_std=True) samples_prior = gp.sample_y(x_test, 3) # plot plt.figure(figsize=(10, 3)) plt.subplot(1, 2, 1) plt.plot(x_test, mu_prior) plt.fill_between(x_test.ravel(), mu_prior - sd_prior, mu_prior + sd_prior, color='aliceblue') plt.plot(x_test, samples_prior, '--') plt.title('Prior') # Fit x_train = np.array([-4, -3, -2, -1, 1]).reshape(-1, 1) y_train = np.sin(x_train) gp.fit(x_train, y_train) # posterior mu_post, sd_post = gp.predict(x_test, return_std=True) mu_post = mu_post.reshape(-1) samples_post = np.squeeze(gp.sample_y(x_test, 3)) # plot plt.subplot(1, 2, 2) plt.plot(x_test, mu_post) plt.fill_between(x_test.ravel(), mu_post - sd_post, mu_post + sd_post, color='aliceblue') plt.plot(x_test, samples_post, '--') plt.scatter(x_train, y_train, c='blue', s=50) plt.title('Posterior') plt.show() print("gp.kernel_", gp.kernel_) print("gp.log_marginal_likelihood:", gp.log_marginal_likelihood(gp.kernel_.theta)) print('-'*50, '
')> Izhod:
RBF
gp.kernel_ RBF(length_scale=1,93)
gp.log_marginal_likelihood: -3,444937833462133
-------------------------------------------------- -
Racionalni kvadrat

gp.kernel_ RationalQuadratic(alpha=1e+05, length_scale=1,93)
gp.log_marginal_likelihood: -3,4449718909150966
--------------------------------------------------
ExpSineSquared

jedro napake segmentacije odloženo
gp.kernel_ ExpSineSquared(length_scale=0,000524, periodičnost=2,31e+04)
gp.log_marginal_likelihood: -3,4449381454930217
--------------------------------------------------
Dot Product

gp.kernel_ DotProduct(sigma_0=0,998) ** 2
gp.log_marginal_likelihood: -150204291.56018084
--------------------------------------------------
Materinski

gp.kernel_ Matern(length_scale=1,99, nu=1,5)
gp.log_marginal_likelihood: -5.131637070524745
--------------------------------------------------
Koda se začne z zanko čez različne funkcije jedra, navedene na seznamu kernel_. Gaussov procesni regresor (gp) je narejen z uporabo določenega jedra za vsako jedro. Za Gaussov proces to vzpostavi kovariančno strukturo. Da bi ocenili prejšnjo porazdelitev, se vzpostavi niz testnih vhodnih točk, imenovanih x_test, z vrednostmi v razponu od -5 do 5. Ta niz točk se pretvori v stolpčni vektor.
oblikovalski vzorci v Javi
Z uporabo metode gp.predict sta povprečje predhodne porazdelitve (mu_prior) in standardni odklon (sd_prior) določena na vsaki testni točki. Vrednosti standardnega odstopanja se zahtevajo z možnostjo return_std=True. gp.sample_y (x_test, 3) se uporablja za pridobitev treh vzorcev funkcij iz prejšnje distribucije.
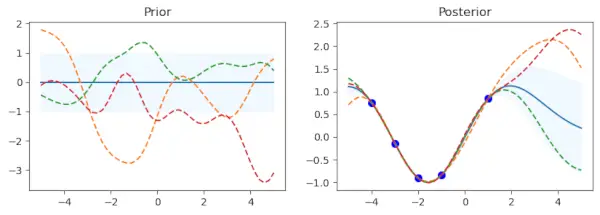
Prvi podgraf prikazuje povprečje prejšnje porazdelitve s standardnim odklonom, ki ga predstavlja zasenčeno območje. Vzorci so prikazani kot črtkane črte, medtem ko je povprečje prikazano kot polna črta. Obstaja podzaplet, imenovan Prior. Obstaja določen nabor podatkovnih točk za vadbo (x_train) in ciljnih vrednosti (y_train), ki jim pripadajo. Model Gaussovega procesa je prilagojen z uporabo teh točk (gp.fit(x_train, y_train)). Pet podatkovnih točk z ustreznimi sinusnimi vrednostmi sestavlja podatke o usposabljanju v tej kodi.
Po fazi prilagajanja podatkov o usposabljanju postopek izračuna srednjo vrednost posteriorne porazdelitve (mu_post) in standardno deviacijo (sd_post) za iste testne točke (x_test). gp.sample_y(x_test, 3) se uporablja tudi za izdelavo funkcijskih vzorcev iz posteriorne porazdelitve. Drugi podgraf prekriva vzorčene funkcije kot pikčaste črte in prikazuje povprečje posteriorne porazdelitve, zasenčeno s standardnim odklonom. V modri barvi so podatkovne točke o vadbi. Podzaplet ima ime Posterior.
Če želite videti prejšnje in zadnje risbe za trenutno jedro in pridobiti vizualno razumevanje vedenja modela, pokličite Matplotlibovo funkcijo plt.show().
Koda prikazuje podrobnosti o trenutnem jedru, kot je gp.kernel_, ki označuje trenutno uporabljeno jedro in gp.log_marginal_likelihood (gp.kernel_.theta), ki daje dnevniku mejno verjetnost modela, ki uporablja trenutno jedro, po vsakem nizu predhodnih in posteriornih grafov.
Prednosti regresije Gaussovega procesa (GPR)
Gaussova procesna regresija (GPR) ima številne prednosti v številnih aplikacijah:
- GPR zagotavlja verjetnostni okvir za regresijo, kar pomeni, da ne daje samo točkovnih ocen, temveč zagotavlja tudi ocene negotovosti za napovedi.
- Je zelo prilagodljiv in lahko zajame kompleksna razmerja v podatkih.
- GPR je mogoče prilagoditi različnim aplikacijam, vključno z napovedovanjem časovnih vrst, optimizacijo in Bayesovo optimizacijo.
Izzivi regresije Gaussovega procesa (GPR)
- GPR je lahko računsko drag, če imamo opravka z velikimi nabori podatkov, saj je potrebna inverzija kovariančne matrike.
- Izbira funkcije jedra in njenih hiperparametrov lahko pomembno vpliva na zmogljivost modela.
Dobri primeri aplikacij GPR
- Napoved tečaja delnice: GPR se lahko uporablja za modeliranje in napovedovanje cen delnic ob upoštevanju nestanovitnosti in negotovosti na finančnih trgih.
- Računalniški poskusi: GPR je uporaben pri optimizaciji kompleksnih simulacij z modeliranjem vhodno-izhodnih razmerij in prepoznavanjem najvplivnejših parametrov.
- Odkrivanje nepravilnosti: GPR je mogoče uporabiti za odkrivanje anomalij, kjer identificira nenavadne vzorce v podatkih časovnih vrst z zajemanjem običajnih porazdelitev podatkov.
Zaključek
Skratka, regresija Gaussovega procesa je dragoceno orodje za analizo podatkov in napovedovanje v situacijah, kjer je razumevanje negotovosti v napovedih bistveno. Z izkoriščanjem verjetnostnega modeliranja in funkcij jedra lahko GPR zagotovi natančne in razložljive rezultate. Vendar pa je pri izvajanju GPR v praksi ključnega pomena upoštevati računske stroške in potrebo po prispevku strokovnjakov.
