A Binarna kopica je popolno binarno drevo ki se uporablja za učinkovito shranjevanje podatkov, da se na podlagi njegove strukture pridobi največji ali najmanjši element.
Binarna kopica je najmanjša ali največja kopica. V minimalni binarni kopici mora biti ključ v korenu minimalen med vsemi ključi, prisotnimi v binarni kopici. Ista lastnost mora biti rekurzivno resnična za vsa vozlišča v binarnem drevesu. Max Binary Heap je podoben MinHeap.
Primeri minimalne kopice:
10 10
/ /
20 100 15 30
/ / /
30 40 50 100 40
Kako je predstavljena binarna kopica?
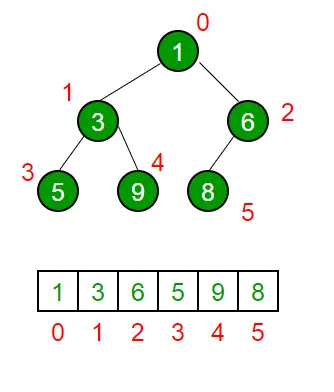
Binarna kopica je a Popolno binarno drevo . Binarna kopica je običajno predstavljena kot niz.
- Korenski element bo na Arr[0].
- Spodnja tabela prikazuje indekse drugih vozlišč za ithvozlišče, tj. Arr[i]:
| Arr[(i-1)/2] | Vrne nadrejeno vozlišče |
| Arr[(2*i)+1] | Vrne levo podrejeno vozlišče |
| Arr[(2*i)+2] | Vrne desno podrejeno vozlišče |
Metoda prehoda, ki se uporablja za doseganje predstavitve polja, je Level Order Traversal . Prosimo, glejte Matrična predstavitev binarne kopice za podrobnosti.
Operacije na kopici:
Spodaj je nekaj standardnih operacij na minimalni kopici:
- getMin(): Vrne korenski element Min Heap. Čas Kompleksnost te operacije je O(1) . V primeru maxheapa bi bilo getMax() .
- ekstraktMin() : Odstrani najmanjši element iz MinHeap. Časovna zapletenost te operacije je O(log N) ker mora ta operacija ohraniti lastnost kopice (s klicem heapify() ) po odstranitvi korena.
- zmanjšajKey() : Zmanjša vrednost ključa. Časovna zahtevnost te operacije je O(log N) . Če je zmanjšana vrednost ključa vozlišča večja od nadrejenega vozlišča, nam ni treba storiti ničesar. V nasprotnem primeru moramo iti navzgor, da popravimo kršeno lastnost kopice.
- vstavi() : Vstavljanje novega ključa traja O(log N) čas. Na koncu drevesa dodamo nov ključ. Če je novi ključ večji od nadrejenega, nam ni treba storiti ničesar. V nasprotnem primeru moramo iti navzgor, da popravimo kršeno lastnost kopice.
- izbrisati() : Tudi brisanje ključa traja O(log N) čas. Ključ za brisanje zamenjamo z minimalnim neskončnim s klicem zmanjšajKey() . Po reduceKey() mora minus neskončna vrednost doseči koren, zato kličemo ekstraktMin() da odstranite ključ.
Spodaj je implementacija osnovnih operacij kopice.
C++
// A C++ program to demonstrate common Binary Heap Operations> #include> #include> using> namespace> std;> > // Prototype of a utility function to swap two integers> void> swap(>int> *x,>int> *y);> > // A class for Min Heap> class> MinHeap> {> >int> *harr;>// pointer to array of elements in heap> >int> capacity;>// maximum possible size of min heap> >int> heap_size;>// Current number of elements in min heap> public>:> >// Constructor> >MinHeap(>int> capacity);> > >// to heapify a subtree with the root at given index> >void> MinHeapify(>int> i);> > >int> parent(>int> i) {>return> (i-1)/2; }> > >// to get index of left child of node at index i> >int> left(>int> i) {>return> (2*i + 1); }> > >// to get index of right child of node at index i> >int> right(>int> i) {>return> (2*i + 2); }> > >// to extract the root which is the minimum element> >int> extractMin();> > >// Decreases key value of key at index i to new_val> >void> decreaseKey(>int> i,>int> new_val);> > >// Returns the minimum key (key at root) from min heap> >int> getMin() {>return> harr[0]; }> > >// Deletes a key stored at index i> >void> deleteKey(>int> i);> > >// Inserts a new key 'k'> >void> insertKey(>int> k);> };> > // Constructor: Builds a heap from a given array a[] of given size> MinHeap::MinHeap(>int> cap)> {> >heap_size = 0;> >capacity = cap;> >harr =>new> int>[cap];> }> > // Inserts a new key 'k'> void> MinHeap::insertKey(>int> k)> {> >if> (heap_size == capacity)> >{> >cout <<>'
Overflow: Could not insertKey
'>;> >return>;> >}> > >// First insert the new key at the end> >heap_size++;> >int> i = heap_size - 1;> >harr[i] = k;> > >// Fix the min heap property if it is violated> >while> (i != 0 && harr[parent(i)]>harr[i])> >{> >swap(&harr[i], &harr[parent(i)]);> >i = parent(i);> >}> }> > // Decreases value of key at index 'i' to new_val. It is assumed that> // new_val is smaller than harr[i].> void> MinHeap::decreaseKey(>int> i,>int> new_val)> {> >harr[i] = new_val;> >while> (i != 0 && harr[parent(i)]>harr[i])> >{> >swap(&harr[i], &harr[parent(i)]);> >i = parent(i);> >}> }> > // Method to remove minimum element (or root) from min heap> int> MinHeap::extractMin()> {> >if> (heap_size <= 0)> >return> INT_MAX;> >if> (heap_size == 1)> >{> >heap_size--;> >return> harr[0];> >}> > >// Store the minimum value, and remove it from heap> >int> root = harr[0];> >harr[0] = harr[heap_size-1];> >heap_size--;> >MinHeapify(0);> > >return> root;> }> > > // This function deletes key at index i. It first reduced value to minus> // infinite, then calls extractMin()> void> MinHeap::deleteKey(>int> i)> {> >decreaseKey(i, INT_MIN);> >extractMin();> }> > // A recursive method to heapify a subtree with the root at given index> // This method assumes that the subtrees are already heapified> void> MinHeap::MinHeapify(>int> i)> {> >int> l = left(i);> >int> r = right(i);> >int> smallest = i;> >if> (l smallest = l; if (r smallest = r; if (smallest != i) { swap(&harr[i], &harr[smallest]); MinHeapify(smallest); } } // A utility function to swap two elements void swap(int *x, int *y) { int temp = *x; *x = *y; *y = temp; } // Driver program to test above functions int main() { MinHeap h(11); h.insertKey(3); h.insertKey(2); h.deleteKey(1); h.insertKey(15); h.insertKey(5); h.insertKey(4); h.insertKey(45); cout << h.extractMin() << ' '; cout << h.getMin() << ' '; h.decreaseKey(2, 1); cout << h.getMin(); return 0; }> |
>
>
niz v javanskih metodah
Java
// Java program for the above approach> import> java.util.*;> > // A class for Min Heap> class> MinHeap {> > >// To store array of elements in heap> >private> int>[] heapArray;> > >// max size of the heap> >private> int> capacity;> > >// Current number of elements in the heap> >private> int> current_heap_size;> > >// Constructor> >public> MinHeap(>int> n) {> >capacity = n;> >heapArray =>new> int>[capacity];> >current_heap_size =>0>;> >}> > >// Swapping using reference> >private> void> swap(>int>[] arr,>int> a,>int> b) {> >int> temp = arr[a];> >arr[a] = arr[b];> >arr[b] = temp;> >}> > > >// Get the Parent index for the given index> >private> int> parent(>int> key) {> >return> (key ->1>) />2>;> >}> > >// Get the Left Child index for the given index> >private> int> left(>int> key) {> >return> 2> * key +>1>;> >}> > >// Get the Right Child index for the given index> >private> int> right(>int> key) {> >return> 2> * key +>2>;> >}> > > >// Inserts a new key> >public> boolean> insertKey(>int> key) {> >if> (current_heap_size == capacity) {> > >// heap is full> >return> false>;> >}> > >// First insert the new key at the end> >int> i = current_heap_size;> >heapArray[i] = key;> >current_heap_size++;> > >// Fix the min heap property if it is violated> >while> (i !=>0> && heapArray[i] swap(heapArray, i, parent(i)); i = parent(i); } return true; } // Decreases value of given key to new_val. // It is assumed that new_val is smaller // than heapArray[key]. public void decreaseKey(int key, int new_val) { heapArray[key] = new_val; while (key != 0 && heapArray[key] swap(heapArray, key, parent(key)); key = parent(key); } } // Returns the minimum key (key at // root) from min heap public int getMin() { return heapArray[0]; } // Method to remove minimum element // (or root) from min heap public int extractMin() { if (current_heap_size <= 0) { return Integer.MAX_VALUE; } if (current_heap_size == 1) { current_heap_size--; return heapArray[0]; } // Store the minimum value, // and remove it from heap int root = heapArray[0]; heapArray[0] = heapArray[current_heap_size - 1]; current_heap_size--; MinHeapify(0); return root; } // This function deletes key at the // given index. It first reduced value // to minus infinite, then calls extractMin() public void deleteKey(int key) { decreaseKey(key, Integer.MIN_VALUE); extractMin(); } // A recursive method to heapify a subtree // with the root at given index // This method assumes that the subtrees // are already heapified private void MinHeapify(int key) { int l = left(key); int r = right(key); int smallest = key; if (l smallest = l; } if (r smallest = r; } if (smallest != key) { swap(heapArray, key, smallest); MinHeapify(smallest); } } // Increases value of given key to new_val. // It is assumed that new_val is greater // than heapArray[key]. // Heapify from the given key public void increaseKey(int key, int new_val) { heapArray[key] = new_val; MinHeapify(key); } // Changes value on a key public void changeValueOnAKey(int key, int new_val) { if (heapArray[key] == new_val) { return; } if (heapArray[key] increaseKey(key, new_val); } else { decreaseKey(key, new_val); } } } // Driver Code class MinHeapTest { public static void main(String[] args) { MinHeap h = new MinHeap(11); h.insertKey(3); h.insertKey(2); h.deleteKey(1); h.insertKey(15); h.insertKey(5); h.insertKey(4); h.insertKey(45); System.out.print(h.extractMin() + ' '); System.out.print(h.getMin() + ' '); h.decreaseKey(2, 1); System.out.print(h.getMin()); } } // This code is contributed by rishabmalhdijo> |
>
vikas divyakirti
>
Python
# A Python program to demonstrate common binary heap operations> > # Import the heap functions from python library> from> heapq>import> heappush, heappop, heapify> > # heappop - pop and return the smallest element from heap> # heappush - push the value item onto the heap, maintaining> # heap invarient> # heapify - transform list into heap, in place, in linear time> > # A class for Min Heap> class> MinHeap:> > ># Constructor to initialize a heap> >def> __init__(>self>):> >self>.heap>=> []> > >def> parent(>self>, i):> >return> (i>->1>)>/>2> > ># Inserts a new key 'k'> >def> insertKey(>self>, k):> >heappush(>self>.heap, k)> > ># Decrease value of key at index 'i' to new_val> ># It is assumed that new_val is smaller than heap[i]> >def> decreaseKey(>self>, i, new_val):> >self>.heap[i]>=> new_val> >while>(i !>=> 0> and> self>.heap[>self>.parent(i)]>>self>.heap[i]):> ># Swap heap[i] with heap[parent(i)]> >self>.heap[i] ,>self>.heap[>self>.parent(i)]>=> (> >self>.heap[>self>.parent(i)],>self>.heap[i])> > ># Method to remove minimum element from min heap> >def> extractMin(>self>):> >return> heappop(>self>.heap)> > ># This function deletes key at index i. It first reduces> ># value to minus infinite and then calls extractMin()> >def> deleteKey(>self>, i):> >self>.decreaseKey(i,>float>(>'-inf'>))> >self>.extractMin()> > ># Get the minimum element from the heap> >def> getMin(>self>):> >return> self>.heap[>0>]> > # Driver pgoratm to test above function> heapObj>=> MinHeap()> heapObj.insertKey(>3>)> heapObj.insertKey(>2>)> heapObj.deleteKey(>1>)> heapObj.insertKey(>15>)> heapObj.insertKey(>5>)> heapObj.insertKey(>4>)> heapObj.insertKey(>45>)> > print> heapObj.extractMin(),> print> heapObj.getMin(),> heapObj.decreaseKey(>2>,>1>)> print> heapObj.getMin()> > # This code is contributed by Nikhil Kumar Singh(nickzuck_007)> |
>
>
C#
kateri meseci so q1
// C# program to demonstrate common> // Binary Heap Operations - Min Heap> using> System;> > // A class for Min Heap> class> MinHeap{> > // To store array of elements in heap> public> int>[] heapArray{>get>;>set>; }> > // max size of the heap> public> int> capacity{>get>;>set>; }> > // Current number of elements in the heap> public> int> current_heap_size{>get>;>set>; }> > // Constructor> public> MinHeap(>int> n)> {> >capacity = n;> >heapArray =>new> int>[capacity];> >current_heap_size = 0;> }> > // Swapping using reference> public> static> void> Swap(>ref> T lhs,>ref> T rhs)> {> >T temp = lhs;> >lhs = rhs;> >rhs = temp;> }> > // Get the Parent index for the given index> public> int> Parent(>int> key)> {> >return> (key - 1) / 2;> }> > // Get the Left Child index for the given index> public> int> Left(>int> key)> {> >return> 2 * key + 1;> }> > // Get the Right Child index for the given index> public> int> Right(>int> key)> {> >return> 2 * key + 2;> }> > // Inserts a new key> public> bool> insertKey(>int> key)> {> >if> (current_heap_size == capacity)> >{> > >// heap is full> >return> false>;> >}> > >// First insert the new key at the end> >int> i = current_heap_size;> >heapArray[i] = key;> >current_heap_size++;> > >// Fix the min heap property if it is violated> >while> (i != 0 && heapArray[i] <> >heapArray[Parent(i)])> >{> >Swap(>ref> heapArray[i],> >ref> heapArray[Parent(i)]);> >i = Parent(i);> >}> >return> true>;> }> > // Decreases value of given key to new_val.> // It is assumed that new_val is smaller> // than heapArray[key].> public> void> decreaseKey(>int> key,>int> new_val)> {> >heapArray[key] = new_val;> > >while> (key != 0 && heapArray[key] <> >heapArray[Parent(key)])> >{> >Swap(>ref> heapArray[key],> >ref> heapArray[Parent(key)]);> >key = Parent(key);> >}> }> > // Returns the minimum key (key at> // root) from min heap> public> int> getMin()> {> >return> heapArray[0];> }> > // Method to remove minimum element> // (or root) from min heap> public> int> extractMin()> {> >if> (current_heap_size <= 0)> >{> >return> int>.MaxValue;> >}> > >if> (current_heap_size == 1)> >{> >current_heap_size--;> >return> heapArray[0];> >}> > >// Store the minimum value,> >// and remove it from heap> >int> root = heapArray[0];> > >heapArray[0] = heapArray[current_heap_size - 1];> >current_heap_size--;> >MinHeapify(0);> > >return> root;> }> > // This function deletes key at the> // given index. It first reduced value> // to minus infinite, then calls extractMin()> public> void> deleteKey(>int> key)> {> >decreaseKey(key,>int>.MinValue);> >extractMin();> }> > // A recursive method to heapify a subtree> // with the root at given index> // This method assumes that the subtrees> // are already heapified> public> void> MinHeapify(>int> key)> {> >int> l = Left(key);> >int> r = Right(key);> > >int> smallest = key;> >if> (l heapArray[l] { smallest = l; } if (r heapArray[r] { smallest = r; } if (smallest != key) { Swap(ref heapArray[key], ref heapArray[smallest]); MinHeapify(smallest); } } // Increases value of given key to new_val. // It is assumed that new_val is greater // than heapArray[key]. // Heapify from the given key public void increaseKey(int key, int new_val) { heapArray[key] = new_val; MinHeapify(key); } // Changes value on a key public void changeValueOnAKey(int key, int new_val) { if (heapArray[key] == new_val) { return; } if (heapArray[key] { increaseKey(key, new_val); } else { decreaseKey(key, new_val); } } } static class MinHeapTest{ // Driver code public static void Main(string[] args) { MinHeap h = new MinHeap(11); h.insertKey(3); h.insertKey(2); h.deleteKey(1); h.insertKey(15); h.insertKey(5); h.insertKey(4); h.insertKey(45); Console.Write(h.extractMin() + ' '); Console.Write(h.getMin() + ' '); h.decreaseKey(2, 1); Console.Write(h.getMin()); } } // This code is contributed by // Dinesh Clinton Albert(dineshclinton)> |
>
>
Javascript
// A class for Min Heap> class MinHeap> {> >// Constructor: Builds a heap from a given array a[] of given size> >constructor()> >{> >this>.arr = [];> >}> > >left(i) {> >return> 2*i + 1;> >}> > >right(i) {> >return> 2*i + 2;> >}> > >parent(i){> >return> Math.floor((i - 1)/2)> >}> > >getMin()> >{> >return> this>.arr[0]> >}> > >insert(k)> >{> >let arr =>this>.arr;> >arr.push(k);> > >// Fix the min heap property if it is violated> >let i = arr.length - 1;> >while> (i>0 && arr[>this>.parent(i)]>arr[i])> >{> >let p =>this>.parent(i);> >[arr[i], arr[p]] = [arr[p], arr[i]];> >i = p;> >}> >}> > >// Decreases value of key at index 'i' to new_val.> >// It is assumed that new_val is smaller than arr[i].> >decreaseKey(i, new_val)> >{> >let arr =>this>.arr;> >arr[i] = new_val;> > >while> (i !== 0 && arr[>this>.parent(i)]>arr[i])> >{> >let p =>this>.parent(i);> >[arr[i], arr[p]] = [arr[p], arr[i]];> >i = p;> >}> >}> > >// Method to remove minimum element (or root) from min heap> >extractMin()> >{> >let arr =>this>.arr;> >if> (arr.length == 1) {> >return> arr.pop();> >}> > >// Store the minimum value, and remove it from heap> >let res = arr[0];> >arr[0] = arr[arr.length-1];> >arr.pop();> >this>.MinHeapify(0);> >return> res;> >}> > > >// This function deletes key at index i. It first reduced value to minus> >// infinite, then calls extractMin()> >deleteKey(i)> >{> >this>.decreaseKey(i,>this>.arr[0] - 1);> >this>.extractMin();> >}> > >// A recursive method to heapify a subtree with the root at given index> >// This method assumes that the subtrees are already heapified> >MinHeapify(i)> >{> >let arr =>this>.arr;> >let n = arr.length;> >if> (n === 1) {> >return>;> >}> >let l =>this>.left(i);> >let r =>this>.right(i);> >let smallest = i;> >if> (l smallest = l; if (r smallest = r; if (smallest !== i) { [arr[i], arr[smallest]] = [arr[smallest], arr[i]] this.MinHeapify(smallest); } } } let h = new MinHeap(); h.insert(3); h.insert(2); h.deleteKey(1); h.insert(15); h.insert(5); h.insert(4); h.insert(45); console.log(h.extractMin() + ' '); console.log(h.getMin() + ' '); h.decreaseKey(2, 1); console.log(h.extractMin());> |
>
>Izhod
2 4 1>
Aplikacije Heaps:
- Razvrščanje kopice : Heap Sort uporablja Binary Heap za razvrščanje matrike v času O(nLogn).
- Prednostna čakalna vrsta: Prednostne čakalne vrste je mogoče učinkovito implementirati z uporabo binarne kopice, ker podpira operacije insert(), delete() in extractmax(), reduceKey() v času O(log N). Binomska kopica in Fibonaccijeva kopica sta različici binarne kopice. Te različice prav tako učinkovito izvajajo spajanje.
- Grafični algoritmi: Prednostne čakalne vrste se uporabljajo zlasti v grafičnih algoritmih, kot je Dijkstrova najkrajša pot in Primovo minimalno vpeto drevo .
- Številne težave je mogoče učinkovito rešiti z uporabo Heaps. Glej naslednji primer. a) K-ti največji element v matriki . b) Razvrsti skoraj razvrščeno matriko/ c) Spoji K razvrščenih nizov .
Sorodne povezave:
- Praksa kodiranja na kopici
- Vsi članki na Heap
- PriorityQueue : Implementacija binarne kopice v knjižnici Java
