Prizma je tridimenzionalna trdna figura z dvema enakima koncema. Sestavljen je iz ravnih stranic, podobnih osnov in enakih prerezov. Njegove ploskve so paralelogrami ali pravokotniki brez osnov. Takšna prizma, ki ima tri pravokotne ploskve in dve vzporedni trikotni osnovi, se imenuje trikotna prizma. Trikotne osnove so povezane s stranskimi ploskvami, ki potekajo vzporedno druga z drugo.
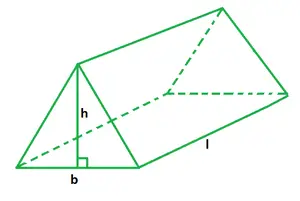
Obseg formule trikotne prizme
Prostornina trikotne prizme je definirana kot prostor znotraj nje ali prostor, ki ga zapolnjuje. Poznavanje osnovne površine in višine trikotne prizme je vse, kar je potrebno za izračun njene prostornine. Prostornina trikotne prizme je enaka zmnožku ploščine osnove in višine prizme, kar je znano tudi kot dolžina prizme. Osnovna ploščina trikotne prizme je enaka polovici zmnožka trikotne osnove in njene nadmorske višine.
Formula
V = (1/2) × b × h × l
kje,
b je trikotna osnova,
h je nadmorska višina prizme,
l je dolžina prizme.
Vzorčne težave
Naloga 1. Poiščite prostornino trikotne prizme, če je njena osnova 6 cm, višina 8 cm in dolžina 12 cm.
rešitev:
Imamo b = 6, h = 8 in l = 12.
niz nizov v programiranju cZ uporabo formule, ki jo imamo,
V = (1/2) × b × h × l
= (1/2) × 6 × 8 × 12
= 3 × 8 × 12
= 288 cu. cm
Naloga 2. Poiščite prostornino trikotne prizme, če je njena osnova 5 cm, višina 7 cm in dolžina 8 cm.
rešitev:
Imamo b = 5, h = 7 in l = 8.
Z uporabo formule, ki jo imamo,
V = (1/2) × b × h × l
kakšna je razlika med megabajtom in gigabajtom= (1/2) × 5 × 7 × 8
= 5 × 7 × 4
= 140 cu. cm
Naloga 3. Poiščite dolžino trikotne prizme, če je njena osnova 6 cm, nadmorska višina 9 cm in prostornina 98 cu. cm.
rešitev:
Imamo b = 6, h = 9 in V = 98.
Z uporabo formule, ki jo imamo,
V = (1/2) × b × h × l
=> 98 = (1/2) × 6 × 9 × l
js set=> 196 = 27l
=> l = 196/27
=> l = 7,25 cm
Naloga 4. Poiščite višino trikotne prizme, če je njena osnova 8 cm, dolžina 14 cm in prostornina 504 cu. cm.
rešitev:
Imamo b = 8, l = 14 in V = 504.
Z uporabo formule, ki jo imamo,
V = (1/2) × b × h × l
=> 504 = (1/2) × 8 × h × 14
=> 504 = 56h
=> h = 504/56
=> v = 9 cm
Naloga 5. Poiščite ploščino osnove trikotne prizme, če je njena dolžina 18 cm, višina 10 cm in prostornina 450 cu. cm.
rešitev:
Imamo l = 18, h = 10 in V = 450.
Z uporabo formule za prostornino, ki jo imamo,
V = (1/2) × b × h × l
delni derivat simbol lateks=> 450 = (1/2) × b × 10 × 18
=> 450 = 90b
=> b = 450/90
=> b = 5 cm
Torej je površina trikotne osnove,
A = (1/2) × b × h
= (1/2) × 5 × 10
= 25 kvadratnih cm
