MOČNO POVEZANE KOMPONENTE - TECHCODEVIEW.COM

Močno povezane komponente (SCC) so temeljni koncept v teoriji grafov in algoritmih. V usmerjenem grafu je a Močno povezana komponenta je podmnožica tock, kjer je vsaka tocka v podmnožici dosegljiva iz vsake druge tocke v isti podmnožici s prečkanjem usmerjenih robov. Iskanje SCC grafa lahko zagotovi pomemben vpogled v strukturo in povezljivost grafa z aplikacijami na različnih področjih, kot je npr. analiza socialnih omrežij, iskanje po spletu in usmerjanje po omrežju . Ta vadnica bo raziskala definicijo, lastnosti in učinkovite algoritme za prepoznavanje močno povezanih komponent v podatkovnih strukturah grafov

spajanje razvrščanje v Javi

Kazalo

Kaj so močno povezane komponente (SCC)?
Zakaj so močno povezane komponente (SCC) pomembne?
Razlika med povezanimi in močno povezanimi komponentami (SCC)
Zakaj običajne metode DFS ni mogoče uporabiti za iskanje močno povezanih komponent?
Povezovanje dveh močno povezanih komponent z enosmernim robom
Pristop surove sile za iskanje močno povezanih komponent
Učinkovit pristop za iskanje močno povezanih komponent (SCC)

1. Kosarajujev algoritem:
2. Tarjanov algoritem:

Zaključek

Kaj so močno povezane komponente (SCC)?

A močno povezana komponenta usmerjenega grafa je maksimalni podgraf, kjer je vsak par vozlišč medsebojno dosegljiv. To pomeni, da za kateri koli dve vozlišči A in B v tem podgrafu obstaja pot od A do B in pot od B do A.

Na primer: Spodnji graf ima dve močno povezani komponenti {1,2,3,4} in {5,6,7}, saj obstaja pot od vsake točke do vsake druge točke v isti močno povezani komponenti.

Močno povezana komponenta

Zakaj so močno povezane komponente (SCC) pomembne?

Razumevanje SCC je ključnega pomena za različne aplikacije, kot so:

Analiza omrežja : Prepoznavanje grozdov tesno povezanih vozlišč.
Optimizacija spletnih pajkov : Določitev delov spletnega grafa, ki so tesno povezani.
Rešitev odvisnosti : V programski opremi razumevanje, kateri moduli so soodvisni.

Razlika med povezanimi in močno povezanimi komponentami ( SCC)

Povezljivost v a neusmerjeni graf se nanaša na to, ali sta dve točki dosegljivi druga od druge ali ne. Za dve točki pravimo, da sta povezani, če je med njima pot. medtem Močno povezani velja samo za usmerjeni grafi . Podgraf usmerjenega grafa se šteje za an Močno povezane komponente (SCC) če in samo če za vsak par vozlišč A in B , obstaja pot od A do B in pot od B do A . Poglejmo, zakaj standardna metoda dfs za iskanje povezanih komponent v grafu ni mogoče uporabiti za določanje močno povezanih komponent.

Razmislite o naslednjem grafu:

Zdaj pa začnimo a dfs klic iz točke 1 za obisk drugih točk.

Zakaj konvencionalne metode DFS ni mogoče uporabiti za iskanje močno povezanih komponent?

Vse točke je mogoče doseči iz točke 1. Toda točke 1 in 5,6,7 ne morejo biti v isti močno povezani komponenti, ker ni usmerjene poti od točke 5,6 ali 7 do točke 1. Graf ima dve močno povezani povezane komponente {1,2,3,4} in {5,6,7}. Tako običajne metode dfs ni mogoče uporabiti za iskanje močno povezanih komponent.

algoritem kabine

Povezovanje dveh močno povezanih komponent z enosmernim robom

Dve različni povezani komponenti postaneta ena sama komponenta, če se doda rob med točko iz ene komponente v točko druge komponente. Vendar to ne velja za močno povezane komponente. Dve močno povezani komponenti ne postaneta ena sama močno povezana komponenta, če obstaja samo enosmerni rob od enega SCC do drugega SCC.

sql count distinct

unidrawio-(2)

Pristop surove sile za iskanje močno povezanih komponent

Preprosta metoda bo za vsako vozlišče i (ki ni del nobene močno komponente) najti vozlišča, ki bodo del močno povezane komponente, ki vsebuje točko i. Dve točki i in j bosta v isti močno povezani komponenti, če obstaja usmerjena pot od točke i do točke j in obratno.

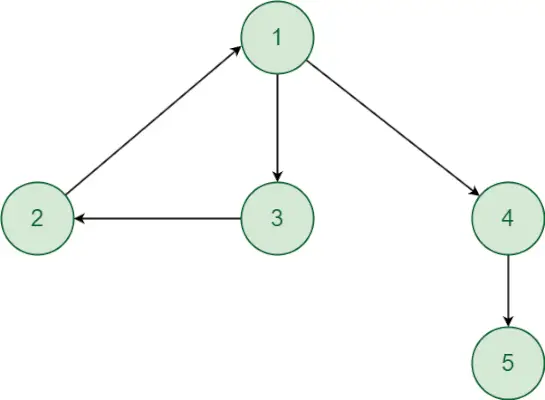
Razumejmo pristop s pomočjo naslednjega primera:

Začenši z točko 1. Obstaja pot od točke 1 do točke 2 in obratno. Podobno obstaja pot od točke 1 do točke 3 in obratno. Torej bosta oglišča 2 in 3 v isti močno povezani komponenti kot oglišče 1. Čeprav obstaja usmerjena pot od oglišča 1 do oglišča 4 in oglišča 5. Vendar ni usmerjene poti od oglišča 4,5 do oglišča 1, zato oglišče 4 in 5 ne bosta v isti močno povezani komponenti kot oglišče 1. Tako oglišča 1, 2 in 3 tvorijo močno povezano komponento.
Za Vertex 2 in 3 je že določena močno povezana komponenta.
Za točko 4 obstaja pot od tocke 4 do tocke 5, ni pa poti od tocke 5 do tocke 4. Torej tocki 4 in 5 ne bosta v isti močno povezani komponenti. Tako bosta tako Vertex 4 kot Vertex 5 del ene same močno povezane komponente.
Zato bodo obstajale 3 močno povezane komponente {1,2,3}, {4} in {5}.

Spodaj je izvedba zgornjega pristopa:

C++

 #include  using namespace std; class GFG { public:  // dfs Function to reach destination  bool dfs(int curr, int des, vector>& adj, vektor & vis) { // Če je curr vozlišče cilj vrni true if (curr == des) { return true;  } vis[curr] = 1;  for (auto x : adj[curr]) { if (!vis[x]) { if (dfs(x, des, adj, vis)) { return true;  } } } vrni napačno;  } // Povedati, ali obstaja pot od vira do // cilja bool isPath(int src, int des, vector>& adj) { vektor vis(adj.size() + 1, 0);  vrni dfs(src, des, adj, vis);  } // Funkcija za vrnitev vseh močno povezanih // komponent grafa.  vektor> najdiSCC(int n, vektor>& a) { // Shrani vse močno povezane komponente.  vektor> ans;  // Shrani, ali je vozlišče del katerega koli vektorja // močno povezane komponente je_scc(n + 1, 0);  vektor> adj(n + 1);  za (int i = 0; i< a.size(); i++) {  adj[a[i][0]].push_back(a[i][1]);  }  // Traversing all the vertices  for (int i = 1; i <= n; i++) {  if (!is_scc[i]) {  // If a vertex i is not a part of any SCC  // insert it into a new SCC list and check  // for other vertices whether they can be  // thr part of thidl ist.  vector scc;  scc.push_back(i);  za (int j = i + 1; j<= n; j++) {  // If there is a path from vertex i to  // vertex j and vice versa put vertex j  // into the current SCC list.  if (!is_scc[j] && isPath(i, j, adj)  && isPath(j, i, adj)) {  is_scc[j] = 1;  scc.push_back(j);  }  }  // Insert the SCC containing vertex i into  // the final list.  ans.push_back(scc);  }  }  return ans;  } }; // Driver Code Starts int main() {  GFG obj;  int V = 5;  vector> robovi { { 1, 3 }, { 1, 4 }, { 2, 1 }, { 3, 2 }, { 4, 5 } };  vektor> ans = obj.findSCC(V, robovi);  cout<< 'Strongly Connected Components are:
';  for (auto x : ans) {  for (auto y : x) {  cout << y << ' ';  }  cout << '
';  } }>

Java

 import java.util.ArrayList; import java.util.List; class GFG {  // dfs Function to reach destination  boolean dfs(int curr, int des, List> adj, Seznam vis) { // Če je curr vozlišče cilj vrni true if (curr == des) { return true;  } vis.set(curr, 1);  for (int x : adj.get(curr)) { if (vis.get(x) == 0) { if (dfs(x, des, adj, vis)) { return true;  } } } vrni napačno;  } // Povedati, ali obstaja pot od vira do // cilja boolean isPath(int src, int des, List> adj) { Seznam vis = nov ArrayList(adj.size() + 1);  za (int i = 0; i<= adj.size(); i++) {  vis.add(0);  }  return dfs(src, des, adj, vis);  }  // Function to return all the strongly connected  // component of a graph.  List> najdiSCC(int n, seznam> a) { // Shrani vse močno povezane komponente.  Seznam> ans = nov ArrayList();  // Shrani, ali je vozlišče del katerega koli seznama // močno povezanih komponent is_scc = nov ArrayList(n + 1);  za (int i = 0; i<= n; i++) {  is_scc.add(0);  }  List> adj = nov ArrayList();  za (int i = 0; i<= n; i++) {  adj.add(new ArrayList());  }  for (List rob : a) { adj.get(edge.get(0)).add(edge.get(1));  } // Prečkanje vseh vozlišč za (int i = 1; i<= n; i++) {  if (is_scc.get(i) == 0) {  // If a vertex i is not a part of any SCC  // insert it into a new SCC list and check  // for other vertices whether they can be  // the part of this list.  List scc = nov ArrayList();  scc.add(i);  za (int j = i + 1; j<= n; j++) {  // If there is a path from vertex i to  // vertex j and vice versa, put vertex j  // into the current SCC list.  if (is_scc.get(j) == 0 && isPath(i, j, adj)  && isPath(j, i, adj)) {  is_scc.set(j, 1);  scc.add(j);  }  }  // Insert the SCC containing vertex i into  // the final list.  ans.add(scc);  }  }  return ans;  } } public class Main {  public static void main(String[] args) {  GFG obj = new GFG();  int V = 5;  List> robovi = nov ArrayList();  edges.add(nov ArrayList(List.of(1, 3)));  edges.add(nov ArrayList(List.of(1, 4)));  edges.add(nov ArrayList(List.of(2, 1)));  edges.add(nov ArrayList(List.of(3, 2)));  edges.add(nov ArrayList(List.of(4, 5)));  Seznam> ans = obj.findSCC(V, robovi);  System.out.println('Močno povezane komponente so:');  za (seznam x : ans) { for (int y : x) { System.out.print(y + ' ');  } System.out.println();  } } } // To kodo je prispeval shivamgupta310570>

Python

 class GFG: # dfs Function to reach destination def dfs(self, curr, des, adj, vis): # If current node is the destination, return True if curr == des: return True vis[curr] = 1 for x in adj[curr]: if not vis[x]: if self.dfs(x, des, adj, vis): return True return False # To tell whether there is a path from source to destination def isPath(self, src, des, adj): vis = [0] * (len(adj) + 1) return self.dfs(src, des, adj, vis) # Function to return all the strongly connected components of a graph. def findSCC(self, n, a): # Stores all the strongly connected components. ans = [] # Stores whether a vertex is a part of any Strongly Connected Component is_scc = [0] * (n + 1) adj = [[] for _ in range(n + 1)] for i in range(len(a)): adj[a[i][0]].append(a[i][1]) # Traversing all the vertices for i in range(1, n + 1): if not is_scc[i]: # If a vertex i is not a part of any SCC, insert it into a new SCC list # and check for other vertices whether they can be part of this list. scc = [i] for j in range(i + 1, n + 1): # If there is a path from vertex i to vertex j and vice versa, # put vertex j into the current SCC list. if not is_scc[j] and self.isPath(i, j, adj) and self.isPath(j, i, adj): is_scc[j] = 1 scc.append(j) # Insert the SCC containing vertex i into the final list. ans.append(scc) return ans # Driver Code Starts if __name__ == '__main__': obj = GFG() V = 5 edges = [ [1, 3], [1, 4], [2, 1], [3, 2], [4, 5] ] ans = obj.findSCC(V, edges) print('Strongly Connected Components are:') for x in ans: for y in x: print(y, end=' ') print() # This code is contributed by shivamgupta310570>

 using System; using System.Collections.Generic; class GFG {  // dfs Function to reach destination  public bool Dfs(int curr, int des, List> adj, Seznam vis) { // Če je curr vozlišče cilj, vrni true if (curr == des) { return true;  } vis[curr] = 1;  foreach (var x in adj[curr]) { if (vis[x] == 0) { if (Dfs(x, des, adj, vis)) { return true;  } } } vrni napačno;  } // Povedati, ali obstaja pot od vira do cilja public bool IsPath(int src, int des, List> adj) { var show = nov seznam (prilag. štetje + 1);  za (int i = 0; i< adj.Count + 1; i++)  {  vis.Add(0);  }  return Dfs(src, des, adj, vis);  }  // Function to return all the strongly connected components of a graph  public List> PoiščiSCC(int n, Seznam> a) { // Shrani vse močno povezane komponente var ans = nov seznam>();  // Shrani, ali je vozlišče del katere koli močno povezane komponente var isScc = nov seznam (n + 1);  za (int i = 0; i< n + 1; i++)  {  isScc.Add(0);  }  var adj = new List>(n + 1);  za (int i = 0; i< n + 1; i++)  {  adj.Add(new List ());  } za (int i = 0; i< a.Count; i++)  {  adj[a[i][0]].Add(a[i][1]);  }  // Traversing all the vertices  for (int i = 1; i <= n; i++)  {  if (isScc[i] == 0)  {  // If a vertex i is not a part of any SCC  // insert it into a new SCC list and check  // for other vertices whether they can be  // the part of this list.  var scc = new List ();  scc.Add(i);  za (int j = i + 1; j<= n; j++)  {  // If there is a path from vertex i to  // vertex j and vice versa, put vertex j  // into the current SCC list.  if (isScc[j] == 0 && IsPath(i, j, adj) && IsPath(j, i, adj))  {  isScc[j] = 1;  scc.Add(j);  }  }  // Insert the SCC containing vertex i into  // the final list.  ans.Add(scc);  }  }  return ans;  } } // Driver Code Starts class Program {  static void Main(string[] args)  {  GFG obj = new GFG();  int V = 5;  List> robovi = nov seznam> { nov seznam { 1, 3 }, nov seznam { 1, 4 }, nov seznam { 2, 1 }, nov seznam { 3, 2 }, nov seznam { 4, 5 } };  Seznam> ans = obj.FindSCC(V, robovi);  Console.WriteLine('Močno povezane komponente so:');  foreach (var x in ans) { foreach (var y in x) { Console.Write(y + ' ');  } Console.WriteLine();  } } } // To kodo je prispeval shivamgupta310570>

Javascript

 class GFG {  // Function to reach the destination using DFS  dfs(curr, des, adj, vis) {  // If the current node is the destination, return true  if (curr === des) {  return true;  }  vis[curr] = 1;  for (let x of adj[curr]) {  if (!vis[x]) {  if (this.dfs(x, des, adj, vis)) {  return true;  }  }  }  return false;  }  // Check whether there is a path from source to destination  isPath(src, des, adj) {  const vis = new Array(adj.length + 1).fill(0);  return this.dfs(src, des, adj, vis);  }  // Function to find all strongly connected components of a graph  findSCC(n, a) {  // Stores all strongly connected components  const ans = [];  // Stores whether a vertex is part of any Strongly Connected Component  const is_scc = new Array(n + 1).fill(0);  const adj = new Array(n + 1).fill().map(() =>[]);  za (naj bo i = 0; i< a.length; i++) {  adj[a[i][0]].push(a[i][1]);  }  // Traversing all the vertices  for (let i = 1; i <= n; i++) {  if (!is_scc[i]) {  // If a vertex i is not part of any SCC,  // insert it into a new SCC list and check  // for other vertices that can be part of this list.  const scc = [i];  for (let j = i + 1; j <= n; j++) {  // If there is a path from vertex i to  // vertex j and vice versa, put vertex j  // into the current SCC list.  if (!is_scc[j] && this.isPath(i, j, adj) && this.isPath(j, i, adj)) {  is_scc[j] = 1;  scc.push(j);  }  }  // Insert the SCC containing vertex i into the final list.  ans.push(scc);  }  }  return ans;  } } // Driver Code Starts const obj = new GFG(); const V = 5; const edges = [  [1, 3], [1, 4], [2, 1], [3, 2], [4, 5] ]; const ans = obj.findSCC(V, edges); console.log('Strongly Connected Components are:'); for (let x of ans) {  console.log(x.join(' ')); } // This code is contributed by shivamgupta310570>

Izhod

Strongly Connected Components are: 1 2 3 4 5>

Časovna kompleksnost: O(n * (n + m)), ker za vsak par vozlišč preverjamo, ali obstaja pot med njima.
Pomožni prostor: O(N)

pretvarjanje niza v celo število

Učinkovit pristop za iskanje močno povezanih komponent (SCC)

Za iskanje SCC v grafu lahko uporabimo algoritme, kot je Kosarajujev algoritem oz Tarjanov algoritem . Raziščimo te algoritme korak za korakom.

1. Kosarajujev algoritem :

Kosarajujev algoritem vključuje dve glavni fazi:

Izvajanje iskanja najprej v globino (DFS) na izvirnem grafu :
- Najprej naredimo DFS na izvirnem grafu in zabeležimo končne čase vozlišč (tj. čas, ko DFS konča celotno raziskovanje vozlišča).
Izvajanje DFS na transponiranem grafu :
- Nato obrnemo smer vseh robov v grafu, da ustvarimo transponirani graf.
- Nato izvedemo DFS na transponiranem grafu, pri čemer upoštevamo vozlišča v padajočem vrstnem redu njihovih končnih časov, zabeleženih v prvi fazi.
- Vsako prečkanje DFS v tej fazi nam bo dalo en SCC.

Tukaj je poenostavljena različica Kosarajujevega algoritma:

DFS na izvirnem grafu : Zabeležite končne čase.
Transponirajte graf : Obrnite vse robove.
DFS na transponiranem grafu : Za iskanje SCC-jev obdelajte vozlišča po padajočem končnem času.

2. Tarjanov algoritem :

Tarjanov algoritem je učinkovitejši, ker najde SCC v enem prehodu DFS z uporabo sklada in nekaj dodatnega knjigovodstva:

Prehod DFS : Med DFS vzdržujte indeks za vsako vozlišče in najmanjši indeks (vrednost nizke povezave), ki ga je mogoče doseči iz vozlišča.
Stack : Spremljajte vozlišča, ki so trenutno v rekurzivnem skladu (del trenutnega SCC, ki se raziskuje).
Prepoznavanje SCC : Ko je vrednost nizke povezave vozlišča enaka njegovemu indeksu, to pomeni, da smo našli SCC. Izstopite vsa vozlišča iz sklada, dokler ne dosežemo trenutnega vozlišča.

Tukaj je poenostavljen oris Tarjanovega algoritma:

Inicializirajindex>na 0.
Za vsako neobiskano vozlišče izvedite DFS.
- Nastavite indeks vozlišča in vrednost nizke povezave.
- Potisnite vozlišče na sklad.
- Za vsako sosednje vozlišče izvedite DFS, če ni obiskano, ali posodobite vrednost nizke povezave, če je v skladu.
- Če je vrednost nizke povezave vozlišča enaka njegovemu indeksu, odstranite vozlišča iz sklada, da oblikujete SCC.

Zaključek

Razumevanje in iskanje močno povezane komponente v usmerjenem grafu je bistvenega pomena za številne aplikacije v računalništvu. Kosarajevih in Tarjanova algoritmi so učinkoviti načini za prepoznavanje SCC, vsak s svojim pristopom in prednostmi. Z obvladovanjem teh konceptov lahko bolje analizirate in optimizirate strukturo in obnašanje kompleksnih omrežij.