Standardna oblika parabole je y = ax2+ bx + c, kjer so a, b in c realna števila in a ni enako nič. Parabola je definirana kot množica vseh točk v ravnini, ki so enako oddaljene od fiksne črte in fiksne točke v ravnini.
V tem članku bomo podrobno razumeli, kaj je parabola, standardno enačbo parabole, povezane primere in druge.
Kazalo
Kaj je parabola?
Parabola je stožčasti prerez, definiran kot niz vseh točk, ki so enako oddaljene od točke, imenovane žarišče, in premice, imenovane direktrisa. Standardne enačbe za parabolo so odvisne od njene usmerjenosti (smeri odpiranja) in položaja.
Enačba parabole
Enačbo parabole lahko zapišemo v standardni ali splošni obliki in obe dodamo spodaj:
Splošne enačbe parabole
Splošna enačba parabole je,
y = 4a(x – h) 2 + k
(ali)
x = 4a(y – k) 2 + h
Kjer je (h, k) oglišče parabole.
Standardne enačbe parabole
Standardna enačba parabole je,
y = sekira 2 + bx + c
(ali)
x = je 2 + avtor + c
kjer a nikoli ne more biti nič.
Deli parabole
Nekateri pomembni izrazi in deli parabole so:
- Fokus: Fokus je fiksna točka parabole.
- Directrix: Direktrisa parabole je premica, pravokotna na os parabole.
- Fokalni akord: Tetiva, ki gre skozi žarišče parabole in seka parabolo na dveh različnih točkah, se imenuje žariščna tetiva.
- Goriščna razdalja: Goriščna razdalja je razdalja točke (x1, in1) na parabolo iz žarišča.
- Desna stran: Latus rectum je žariščna tetiva, ki poteka skozi žarišče parabole in je pravokotna na os parabole. Dolžina latus rektuma je LL’ = 4a.
- Ekscentričnost: Razmerje med oddaljenostjo točke od gorišča in njeno oddaljenostjo od direktrise imenujemo ekscentričnost (e). Za parabolo je ekscentričnost enaka 1, tj. e = 1.
Parabola ima štiri standardne enačbe, ki temeljijo na orientaciji parabole in njene osi. Vsaka parabola ima drugačno prečno os in konjugirano os.
| Enačba parabole | Parabola | Formule parametrov parabole |
|---|---|---|
| in 2 = 4 ax | 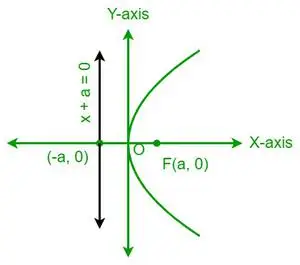 Vodoravna parabola |
|
| in 2 = -4ax |  Vodoravna parabola |
|
| x 2 = 4ay |  Navpična parabola |
|
| x 2 = -4ay |  Navpična parabola |
|
Spodaj so opažanja iz standardne oblike enačb parabole:
- Parabola je simetrična glede na svojo os. Na primer, y2= 4ax je simetričen glede na os x, medtem ko je x2= 4ay je simetričen glede na os y.
- Če je parabola simetrična glede na os x, se parabola odpre v desno, če je x-koeficient pozitiven, in proti levi, če je x-koeficient negativen.
- Če je parabola simetrična glede na os y, se parabola odpira navzgor, če je y-koeficient pozitiven, in navzdol, če je y-koeficient negativen.
Sledijo standardne enačbe parabole, ko je simetrijska os vzporedna z osjo x ali osjo y in oglišče ni v izhodišču.
| Enačba parabole | Parabola | Formule parametrov parabole |
|---|---|---|
| (in – k)2= 4a(x – h) |  Vodoravna parabola |
|
| (in – k)2= -4a(x – h) |  Vodoravna parabola |
|
| (x – h)2= 4a(y – k) |  Navpična parabola |
|
| (x – h)2= -4a(y – k) |  Navpična parabola |
|
Enačba izpeljave parabole
Naj bo P točka na paraboli, katere koordinate so (x, y). Iz definicije parabole je razdalja točke P do gorišča (F) enaka razdalji iste točke P do direktrise parabole. Zdaj pa si oglejmo točko X na direktrisi, katere koordinate so (-a, y).
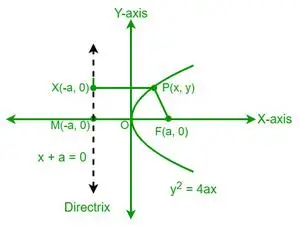
Iz definicije ekscentričnosti parabole imamo
e = PF/PX = 1
⇒ PF = PX
Koordinate žarišča so (a, 0). Zdaj lahko z uporabo formule za koordinatno razdaljo poiščemo razdaljo točke P (x, y) do žarišča F (a, 0).
PF = √[(x – a)2+ (in – 0)2]
⇒ PF = √[(x – a)2+ in2] ------ (1)
Enačba direktrise je x + a = 0. Za iskanje razdalje PX uporabimo formulo za pravokotno razdaljo.
PX = (x + a)/√[12+02]
⇒ PX = x +a —————— (2)
Vemo že, da je PF = PX. Torej enačite enačbi (1) in (2).
√[(x – a)2+ in2] = (x + a)
S kvadriranjem na obeh straneh dobimo,
⇒ [(x – a)2+ in2] = (x + a)2
⇒ x2+ a2– 2ax + y2= x2+ a2+ 2 ax
⇒ in2– 2ax = 2ax
⇒ in2= 2ax + 2ax ⇒ in 2 = 4 ax
Tako smo izpeljali enačbo parabole. Podobno lahko izpeljemo standardne enačbe ostalih treh parabol.
- in2= -4ax
- x2= 4ay
- x2= -4ay
in 2 = 4ax in 2 = -4ax, x 2 = 4ay in x 2 = -4ay so standardne enačbe parabole.
Članki, povezani s parabolo:
- Enačba kroga
- Enačba elipse
- Enačba hiperbole
- Uporaba parabole v resničnem življenju
Primeri enačbe parabole
Primer1: Poiščite dolžino latus rektuma, žarišča in vrha, če je enačba parabole y 2 = 12x.
rešitev:
podano,
Enačba parabole je y2= 12x
S primerjavo dane enačbe s standardno obliko y2= 4 ax
4a = 12
⇒ a = 12/4 = 3
Vemo, da
Desna stran parabole = 4a = 4 (3) = 12
Sedaj, fokus parabole = (a, 0) = (3, 0)
Vrh dane parabole = (0, 0)
Primer 2: Poiščite enačbo parabole, ki je simetrična glede na os X in poteka skozi točko (-4, 5).
rešitev:
podano,
Parabola je simetrična glede na os X in ima vrh v izhodišču.
Tako je lahko enačba oblike y2= 4ax ali y2= -4ax, kjer je predznak odvisen od tega, ali se parabola odpira proti levi ali desni strani.
Parabola se mora odpreti levo, ker gre skozi (-4, 5), ki leži v drugem kvadrantu.
Torej bo enačba: y2= -4ax
Zamenjava (-4, 5) v zgornji enačbi,
⇒ (5)2= -4a(-4)
⇒ 25 = 16a
⇒ a = 25/16
Zato je enačba parabole: y2= -4(25/16)x (ali) 4y2= -25x.
Primer 3: Poiščite koordinate žarišča, osi, enačbe direktrise in latus rectum parabole x 2 = 16 let.
rešitev:
podano,
Enačba parabole je: x2= 16 let
S primerjavo dane enačbe s standardno obliko x2= 4ay,
4a = 16 ⇒ a = 4
Koeficient y je pozitiven, zato se parabola odpira navzgor.
Poleg tega je simetrijska os vzdolž pozitivne osi Y.
torej
Gorišče parabole je (a, 0) = (4, 0).
Enačba direktrise je y = -a, tj. y = -4 ali y + 4 = 0.
Dolžina latus rektuma = 4a = 4(4) = 16.
Primer 4: Poiščite dolžino latus rektuma, žarišča in vrha, če je enačba parabole 2(x-2) 2 + 16 = y.
rešitev:
podano,
Enačba parabole je 2(x-2)2+ 16 = in
S primerjavo dane enačbe s splošno enačbo parabole y = a(x – h)2+ k, dobimo
a = 2
(h, k) = (2, 16)
Vemo, da
Dolžina latus rektuma parabole = 4a
= 4(2) = 8
Zdaj fokus = (a, 0) = (2, 0)
Zdaj, Vertex = (2, 16)
Primer 5: Enačba parabole je x 2 – 12x + 4y – 24 = 0, nato poiščite njegovo oglišče, gorišče in direktriso.
rešitev:
podano,
Enačba parabole je x2– 12x + 4y – 24 = 0
⇒ x2– 12x + 36 – 36 + 4y – 24 = 0
⇒ (x – 6)2+ 4y – 60 = 0
⇒ (x – 6)2= -4(y + 15)
Dobljena enačba je v obliki (x – h)2= -4a(y – k)
-4a = -4 ⇒ a = 1
Torej, oglišče = (h, k) = (6, – 15)
Fokus = (h, k – a) = (6, -15-1) = (6, -16)
Enačba direktrise je y = k + a
⇒ y = -15 + 1 ⇒ y = -14
⇒ y + 14 = 0
Pogosta vprašanja o enačbi parabole
Kako najdete standardno enačbo parabole?
Standardna oblika parabole je y2= 4ax ali x2= 4ay.
Kaj je normalna enačba parabole?
Enačba normale na parabolo y2= 4ax z naklonom m je podan kot: y = mx – 2 zjutraj – zjutraj 3
Kako najdete vrh parabole?
Za dano parabolo: y = ax2+ bx + c njeno oglišče je mogoče najti s formulo x = − b/2a. Vstavite to vrednost x nazaj v enačbo, da poiščete ustrezno y-koordinato.
preity zinta
