V računalništvu obstajajo nekateri problemi, katerih rešitve še niso najdene, problemi so razdeljeni v razrede, znane kot Razredi kompleksnosti . V teoriji kompleksnosti je razred kompleksnosti niz problemov s sorodno kompleksnostjo. Ti razredi znanstvenikom pomagajo pri združevanju problemov glede na to, koliko časa in prostora potrebujejo za reševanje problemov in preverjanje rešitev. To je veja teorije računanja, ki se ukvarja z viri, potrebnimi za rešitev problema.
kako pridobiti skrite aplikacije
Skupna vira sta čas in prostor, kar pomeni, koliko časa algoritem potrebuje za rešitev problema in ustrezno uporabo pomnilnika.
- Časovna kompleksnost algoritma se uporablja za opis števila korakov, potrebnih za rešitev problema, lahko pa se uporablja tudi za opis, koliko časa traja, da se preveri odgovor.
- Prostorska kompleksnost algoritma opisuje, koliko pomnilnika je potrebno za delovanje algoritma.
Razredi kompleksnosti so uporabni pri organiziranju podobnih vrst problemov.
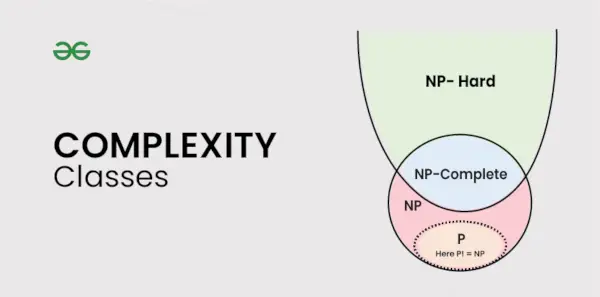
Vrste kompleksnih razredov
Ta članek obravnava naslednje razrede kompleksnosti:
- P razred
- Razred NP
- Razred CoNP
- NP-težko
- NP-popoln
P razred
P v razredu P pomeni Polinomski čas. Je zbirka problemov odločanja (problemov z odgovorom da ali ne), ki jih lahko reši deterministični stroj v polinomskem času.
Lastnosti:
- Rešitev za P problem s je enostavno najti.
- p je pogosto razred računalniških problemov, ki so rešljivi in sledljivi. Tractable pomeni, da je probleme mogoče rešiti tako v teoriji kot v praksi. Toda problemi, ki jih je mogoče rešiti v teoriji, v praksi pa ne, so znani kot nerešljivi.
Ta razred vsebuje veliko težav:
- Računanje največjega skupnega delitelja.
- Iskanje največjega ujemanja.
- Spoji Razvrsti
Razred NP
NP v razredu NP pomeni Nedeterministični polinomski čas . Je zbirka problemov odločanja, ki jih lahko reši nedeterministični stroj v polinomskem času.
Lastnosti:
2 proti 1 multiplekser
- Rešitve razreda NP je težko najti, saj jih rešuje nedeterministični stroj, vendar je rešitve enostavno preveriti.
- Probleme NP je mogoče preveriti s Turingovim strojem v polinomskem času.
primer:
Za boljše razumevanje si oglejmo primer razred NP . Recimo, da ima podjetje skupno 1000 zaposleni, ki imajo edinstvenega zaposlenega osebne izkaznice . Predpostavimo, da obstajajo 200 prostorov, ki so jim na voljo. Izbor od 200 zaposleni morajo biti združeni, vendar ima direktor podjetja podatke nekaterih zaposlenih, ki zaradi osebnih razlogov ne morejo delati v istem prostoru.
To je primer Npr problem. Ker je enostavno preveriti, ali je dana izbira 200 zaposlenih, ki jih je predlagal sodelavec, zadovoljiv ali ne, tj. noben par s seznama sodelavcev se ne pojavi na seznamu, ki ga poda direktor. Vendar se zdi, da je ustvariti tak seznam iz nič tako težko, da je popolnoma nepraktično.
Nakazuje, da če nam nekdo lahko ponudi rešitev problema, lahko najdemo pravilen in nepravilen par v polinomskem času. Tako za Npr razredni problem je možen odgovor, ki ga lahko izračunamo v polinomskem času.
Ta razred vsebuje veliko problemov, ki bi jih želeli učinkovito rešiti:
- Boolov problem zadovoljivosti (SAT).
- Problem Hamiltonove poti.
- Barvanje grafov.
Razred Co-NP
Co-NP pomeni dopolnilo razreda NP. To pomeni, da če je odgovor na problem v Co-NP Ne, potem obstaja dokaz, ki ga je mogoče preveriti v polinomskem času.
Lastnosti:
- Če je problem X v NP, potem je tudi njegov komplement X' v CoNP.
- Za problem NP in CoNP ni treba preveriti vseh odgovorov hkrati v polinomskem času, v polinomskem času je treba preveriti samo en določen odgovor da ali ne, da bo problem v NP ali CoNP.
Nekaj primerov težav za CoNP je:
- Za preverjanje praštevila.
- Faktorizacija celih števil.
NP-trdi razred
NP-težak problem je vsaj tako težak kot najtežji problem v NP in je takšen razred problemov, da se vsak problem v NP zmanjša na NP-težek.
klicanje funkcije js iz html
Lastnosti:
- Vse NP-težke težave niso v NP.
- Dolgo traja njihovo preverjanje. To pomeni, da če je podana rešitev za NP-težko težavo, traja dolgo časa, da se preveri, ali je pravilna ali ne.
- Problem A je NP-težak, če za vsak problem L v NP obstaja polinomska časovna redukcija od L do A.
Nekateri primeri težav v Np-hard so:
- Težava pri ustavljanju.
- Kvalificirane logične formule.
- Ni Hamiltonovega cikla.
NP-polni razred
Problem je NP-popoln, če je hkrati NP in NP-trd. NP-popolni problemi so težki problemi v NP.
Lastnosti:
- NP-popolni problemi so posebni, saj je vsak problem v razredu NP mogoče preoblikovati ali reducirati v NP-popolne probleme v polinomskem času.
- Če bi lahko rešili NP-popoln problem v polinomskem času, bi lahko rešili tudi kateri koli NP problem v polinomskem času.
Nekateri primeri težav vključujejo:
- Hamiltonov cikel.
- Zadovoljljivost.
- Pokrov Vertex .
| Razred kompleksnosti | Značilna lastnost |
| p | Enostavno rešljiv v polinomskem času. |
| Npr | Da, odgovore je mogoče preveriti v polinomskem času. |
| So-NP | Ne, odgovore je mogoče preveriti v polinomskem času. |
| NP-težko | Vse NP-težke težave niso v NP in njihovo preverjanje traja dolgo. |
| NP-popoln | Problem, ki je NP in NP-težak, je NP-popoln. |
