Kaj je Hamiltonov cikel?
Hamiltonov cikel ali krog v grafu G je cikel, ki obišče vsako točko G natanko enkrat in se vrne v začetno točko.
- Če graf vsebuje Hamiltonov cikel, se imenuje Hamiltonov graf drugače je nehamiltonski .
- Iskanje Hamiltonovega cikla v grafu je dobro znano NP-popoln problem , kar pomeni, da ni znanega učinkovitega algoritma za rešitev za vse vrste grafov. Vendar ga je mogoče rešiti za majhne ali posebne vrste grafov.
Problem Hamiltonovega cikla ima praktične aplikacije na različnih področjih, kot je npr logistika, načrtovanje omrežij in računalništvo .
Kaj je Hamiltonova pot?
Hamiltonova pot v grafu G je pot, ki obišče vsako točko G natanko enkrat in Hamiltonova pot ni treba vrniti v začetno točko. To je odprta pot.
- Podobno kot pri Hamiltonov cikel problem, iskanje a Hamiltonova pot v splošnem grafu je tudi NP-popoln in je lahko izziv. Vendar pa je pogosto lažji problem kot iskanje Hamiltonovega cikla.
- Hamiltonove poti imajo aplikacije na različnih področjih, kot npr iskanje optimalnih poti v prometnih omrežjih, načrtovanje vezij in raziskovanje teorije grafov .
Izjava o težavah: Pri danem neusmerjenem grafu je naloga ugotoviti, ali graf vsebuje Hamiltonov cikel ali ne. Če vsebuje, natisne pot.
primer:
Priporočeno: prosimo, rešite ga na VADITE najprej, preden preidete na rešitev.Vnos: graf[][] = {{0, 1, 0, 1, 0},{1, 0, 1, 1, 1},{0, 1, 0, 0, 1},{1, 1, 0, 0, 1}, {0, 1, 1, 1, 0}}
Vnosni graf[][]
kako centrirati sliko na cssIzhod: {0, 1, 2, 4, 3, 0}.
Vnos: graf[][] = {{0, 1, 0, 1, 0},{1, 0, 1, 1, 1},{0, 1, 0, 0, 1},{1, 1, 0, 0, 0}, {0, 1, 1, 0, 0}}
Vnosni graf[][]
Izhod: Rešitev ne obstaja
Naivni algoritem : To težavo je mogoče rešiti s spodnjo idejo:
Generirajte vse možne konfiguracije vozlišč in natisnite konfiguracijo, ki ustreza podanim omejitvam. Tam bo n! (n faktorskih) konfiguracij. Torej bo splošna časovna kompleksnost tega pristopa O(N!).
Uporaba Hamiltonovega cikla Algoritem za povratno sledenje :
Ustvarite prazno matriko poti in dodajte točko 0 temu. Dodajte druga oglišča, začenši od oglišča 1 . Pred dodajanjem vozlišča preverite, ali je sosednje predhodno dodanemu vozlišču in ni že dodano. Če najdemo tako vozlišče, ga dodamo kot del rešitve. Če ne najdemo vozlišča, se vrnemo lažno .
Ilustracije:
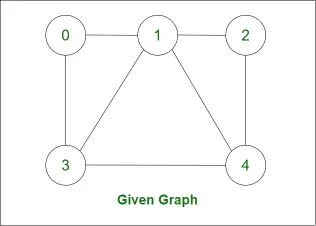
Ugotovimo Hamiltonov cikel za naslednji graf:
- Začnite z vozliščem 0.
- Uporabite DFS za iskanje Hamiltonove poti.
- Ko osnovni primer doseže (tj. skupno število prečkanih vozlišč == V (skupno vozlišče) ):
- Preverite, ali je trenutno vozlišče sosed začetnega vozlišča.
- Kot vozlišče 2 in vozlišče 0 nista soseda drug drugemu, zato se vrnite od njega.
Zagon od začetnega vozlišča 0, ki kliče DFS
- Ker cikla ni mogoče najti na poti {0, 3, 1, 4, 2}. Torej, vrnitev iz vozlišča 2, vozlišča 4.
- Zdaj pa raziščite drugo možnost za vozlišče 1 (tj. vozlišče 2)
- Ko ponovno doseže osnovni pogoj, preveri Hamiltonov cikel
- Ker vozlišče 4 ni sosed vozlišča 0, ponovno cikel ni najden in se vrne.
- Vrnitev iz vozlišča 4, vozlišča 2, vozlišča 1.
- Zdaj pa raziščite druge možnosti za vozlišče 3.
Hamiltonov cikel
- Na Hamiltonovi poti {0,3,4,2,1,0} dobimo cikel, saj je vozlišče 1 sosed vozlišča 0.
- Torej natisnite to ciklično pot.
- To je naš Hamiltonov cikel.
Spodaj je implementacija sledenja nazaj za iskanje Hamiltonovega cikla:
C++ /* C++ program for solution of Hamiltonian Cycle problem using backtracking */ #include using namespace std; // Number of vertices in the graph #define V 5 void printSolution(int path[]); /* A utility function to check if the vertex v can be added at index 'pos' in the Hamiltonian Cycle constructed so far (stored in 'path[]') */ bool isSafe(int v, bool graph[V][V], int path[], int pos) { /* Check if this vertex is an adjacent vertex of the previously added vertex. */ if (graph [path[pos - 1]][ v ] == 0) return false; /* Check if the vertex has already been included. This step can be optimized by creating an array of size V */ for (int i = 0; i < pos; i++) if (path[i] == v) return false; return true; } /* A recursive utility function to solve hamiltonian cycle problem */ bool hamCycleUtil(bool graph[V][V], int path[], int pos) { /* base case: If all vertices are included in Hamiltonian Cycle */ if (pos == V) { // And if there is an edge from the // last included vertex to the first vertex if (graph[path[pos - 1]][path[0]] == 1) return true; else return false; } // Try different vertices as a next candidate // in Hamiltonian Cycle. We don't try for 0 as // we included 0 as starting point in hamCycle() for (int v = 1; v < V; v++) { /* Check if this vertex can be added // to Hamiltonian Cycle */ if (isSafe(v, graph, path, pos)) { path[pos] = v; /* recur to construct rest of the path */ if (hamCycleUtil (graph, path, pos + 1) == true) return true; /* If adding vertex v doesn't lead to a solution, then remove it */ path[pos] = -1; } } /* If no vertex can be added to Hamiltonian Cycle constructed so far, then return false */ return false; } /* This function solves the Hamiltonian Cycle problem using Backtracking. It mainly uses hamCycleUtil() to solve the problem. It returns false if there is no Hamiltonian Cycle possible, otherwise return true and prints the path. Please note that there may be more than one solutions, this function prints one of the feasible solutions. */ bool hamCycle(bool graph[V][V]) { int *path = new int[V]; for (int i = 0; i < V; i++) path[i] = -1; /* Let us put vertex 0 as the first vertex in the path. If there is a Hamiltonian Cycle, then the path can be started from any point of the cycle as the graph is undirected */ path[0] = 0; if (hamCycleUtil(graph, path, 1) == false ) { cout << '
Solution does not exist'; return false; } printSolution(path); return true; } /* A utility function to print solution */ void printSolution(int path[]) { cout << 'Solution Exists:' ' Following is one Hamiltonian Cycle
'; for (int i = 0; i < V; i++) cout << path[i] << ' '; // Let us print the first vertex again // to show the complete cycle cout << path[0] << ' '; cout << endl; } // Driver Code int main() { /* Let us create the following graph (0)--(1)--(2) | / | | / | | / | (3)-------(4) */ bool graph1[V][V] = {{0, 1, 0, 1, 0}, {1, 0, 1, 1, 1}, {0, 1, 0, 0, 1}, {1, 1, 0, 0, 1}, {0, 1, 1, 1, 0}}; // Print the solution hamCycle(graph1); /* Let us create the following graph (0)--(1)--(2) | / | | / | | / | (3) (4) */ bool graph2[V][V] = {{0, 1, 0, 1, 0}, {1, 0, 1, 1, 1}, {0, 1, 0, 0, 1}, {1, 1, 0, 0, 0}, {0, 1, 1, 0, 0}}; // Print the solution hamCycle(graph2); return 0; } // This is code is contributed by rathbhupendra> C++ #include using namespace std; int main() { cout << 'GFG!'; return 0; }> C /* C program for solution of Hamiltonian Cycle problem using backtracking */ #include // Number of vertices in the graph #define V 5 void printSolution(int path[]); /* A utility function to check if the vertex v can be added at index 'pos' in the Hamiltonian Cycle constructed so far (stored in 'path[]') */ int isSafe(int v, int graph[V][V], int path[], int pos) { /* Check if this vertex is an adjacent vertex of the previously added vertex. */ if (graph [ path[pos-1] ][ v ] == 0) return 0; /* Check if the vertex has already been included. This step can be optimized by creating an array of size V */ for (int i = 0; i < pos; i++) if (path[i] == v) return 0; return 1; } /* A recursive utility function to solve hamiltonian cycle problem */ int hamCycleUtil(int graph[V][V], int path[], int pos) { /* base case: If all vertices are included in Hamiltonian Cycle */ if (pos == V) { // And if there is an edge from the last included vertex to the // first vertex if ( graph[ path[pos-1] ][ path[0] ] == 1 ) return 1; else return 0; } // Try different vertices as a next candidate in Hamiltonian Cycle. // We don't try for 0 as we included 0 as starting point in hamCycle() for (int v = 1; v < V; v++) { /* Check if this vertex can be added to Hamiltonian Cycle */ if (isSafe(v, graph, path, pos)) { path[pos] = v; /* recur to construct rest of the path */ if (hamCycleUtil (graph, path, pos+1) == 1) return 1; /* If adding vertex v doesn't lead to a solution, then remove it */ path[pos] = -1; } } /* If no vertex can be added to Hamiltonian Cycle constructed so far, then return false */ return 0; } /* This function solves the Hamiltonian Cycle problem using Backtracking. It mainly uses hamCycleUtil() to solve the problem. It returns false if there is no Hamiltonian Cycle possible, otherwise return true and prints the path. Please note that there may be more than one solutions, this function prints one of the feasible solutions. */ int hamCycle(int graph[V][V]) { int path[V]; for (int i = 0; i < V; i++) path[i] = -1; /* Let us put vertex 0 as the first vertex in the path. If there is a Hamiltonian Cycle, then the path can be started from any point of the cycle as the graph is undirected */ path[0] = 0; if ( hamCycleUtil(graph, path, 1) == 0 ) { printf('
Solution does not exist'); return 0; } printSolution(path); return 1; } /* A utility function to print solution */ void printSolution(int path[]) { printf ('Solution Exists:' ' Following is one Hamiltonian Cycle
'); for (int i = 0; i < V; i++) printf(' %d ', path[i]); // Let us print the first vertex again to show the complete cycle printf(' %d ', path[0]); printf('
'); } // driver program to test above function int main() { /* Let us create the following graph (0)--(1)--(2) | / | | / | | / | (3)-------(4) */ int graph1[V][V] = {{0, 1, 0, 1, 0}, {1, 0, 1, 1, 1}, {0, 1, 0, 0, 1}, {1, 1, 0, 0, 1}, {0, 1, 1, 1, 0}, }; // Print the solution hamCycle(graph1); /* Let us create the following graph (0)--(1)--(2) | / | | / | | / | (3) (4) */ int graph2[V][V] = {{0, 1, 0, 1, 0}, {1, 0, 1, 1, 1}, {0, 1, 0, 0, 1}, {1, 1, 0, 0, 0}, {0, 1, 1, 0, 0}, }; // Print the solution hamCycle(graph2); return 0; }> Java /* Java program for solution of Hamiltonian Cycle problem using backtracking */ class HamiltonianCycle { final int V = 5; int path[]; /* A utility function to check if the vertex v can be added at index 'pos'in the Hamiltonian Cycle constructed so far (stored in 'path[]') */ boolean isSafe(int v, int graph[][], int path[], int pos) { /* Check if this vertex is an adjacent vertex of the previously added vertex. */ if (graph[path[pos - 1]][v] == 0) return false; /* Check if the vertex has already been included. This step can be optimized by creating an array of size V */ for (int i = 0; i < pos; i++) if (path[i] == v) return false; return true; } /* A recursive utility function to solve hamiltonian cycle problem */ boolean hamCycleUtil(int graph[][], int path[], int pos) { /* base case: If all vertices are included in Hamiltonian Cycle */ if (pos == V) { // And if there is an edge from the last included // vertex to the first vertex if (graph[path[pos - 1]][path[0]] == 1) return true; else return false; } // Try different vertices as a next candidate in // Hamiltonian Cycle. We don't try for 0 as we // included 0 as starting point in hamCycle() for (int v = 1; v < V; v++) { /* Check if this vertex can be added to Hamiltonian Cycle */ if (isSafe(v, graph, path, pos)) { path[pos] = v; /* recur to construct rest of the path */ if (hamCycleUtil(graph, path, pos + 1) == true) return true; /* If adding vertex v doesn't lead to a solution, then remove it */ path[pos] = -1; } } /* If no vertex can be added to Hamiltonian Cycle constructed so far, then return false */ return false; } /* This function solves the Hamiltonian Cycle problem using Backtracking. It mainly uses hamCycleUtil() to solve the problem. It returns false if there is no Hamiltonian Cycle possible, otherwise return true and prints the path. Please note that there may be more than one solutions, this function prints one of the feasible solutions. */ int hamCycle(int graph[][]) { path = new int[V]; for (int i = 0; i < V; i++) path[i] = -1; /* Let us put vertex 0 as the first vertex in the path. If there is a Hamiltonian Cycle, then the path can be started from any point of the cycle as the graph is undirected */ path[0] = 0; if (hamCycleUtil(graph, path, 1) == false) { System.out.println('
Solution does not exist'); return 0; } printSolution(path); return 1; } /* A utility function to print solution */ void printSolution(int path[]) { System.out.println('Solution Exists: Following' + ' is one Hamiltonian Cycle'); for (int i = 0; i < V; i++) System.out.print(' ' + path[i] + ' '); // Let us print the first vertex again to show the // complete cycle System.out.println(' ' + path[0] + ' '); } // driver program to test above function public static void main(String args[]) { HamiltonianCycle hamiltonian = new HamiltonianCycle(); /* Let us create the following graph (0)--(1)--(2) | / | | / | | / | (3)-------(4) */ int graph1[][] = {{0, 1, 0, 1, 0}, {1, 0, 1, 1, 1}, {0, 1, 0, 0, 1}, {1, 1, 0, 0, 1}, {0, 1, 1, 1, 0}, }; // Print the solution hamiltonian.hamCycle(graph1); /* Let us create the following graph (0)--(1)--(2) | / | | / | | / | (3) (4) */ int graph2[][] = {{0, 1, 0, 1, 0}, {1, 0, 1, 1, 1}, {0, 1, 0, 0, 1}, {1, 1, 0, 0, 0}, {0, 1, 1, 0, 0}, }; // Print the solution hamiltonian.hamCycle(graph2); } } // This code is contributed by Abhishek Shankhadhar> Python # Python program for solution of # hamiltonian cycle problem class Graph(): def __init__(self, vertices): self.graph = [[0 for column in range(vertices)] for row in range(vertices)] self.V = vertices ''' Check if this vertex is an adjacent vertex of the previously added vertex and is not included in the path earlier ''' def isSafe(self, v, pos, path): # Check if current vertex and last vertex # in path are adjacent if self.graph[ path[pos-1] ][v] == 0: return False # Check if current vertex not already in path for vertex in path: if vertex == v: return False return True # A recursive utility function to solve # hamiltonian cycle problem def hamCycleUtil(self, path, pos): # base case: if all vertices are # included in the path if pos == self.V: # Last vertex must be adjacent to the # first vertex in path to make a cycle if self.graph[ path[pos-1] ][ path[0] ] == 1: return True else: return False # Try different vertices as a next candidate # in Hamiltonian Cycle. We don't try for 0 as # we included 0 as starting point in hamCycle() for v in range(1,self.V): if self.isSafe(v, pos, path) == True: path[pos] = v if self.hamCycleUtil(path, pos+1) == True: return True # Remove current vertex if it doesn't # lead to a solution path[pos] = -1 return False def hamCycle(self): path = [-1] * self.V ''' Let us put vertex 0 as the first vertex in the path. If there is a Hamiltonian Cycle, then the path can be started from any point of the cycle as the graph is undirected ''' path[0] = 0 if self.hamCycleUtil(path,1) == False: print ('Solution does not exist
') return False self.printSolution(path) return True def printSolution(self, path): print ('Solution Exists: Following', 'is one Hamiltonian Cycle') for vertex in path: print (vertex ) # Driver Code ''' Let us create the following graph (0)--(1)--(2) | / | | / | | / | (3)-------(4) ''' g1 = Graph(5) g1.graph = [ [0, 1, 0, 1, 0], [1, 0, 1, 1, 1], [0, 1, 0, 0, 1,],[1, 1, 0, 0, 1], [0, 1, 1, 1, 0], ] # Print the solution g1.hamCycle(); ''' Let us create the following graph (0)--(1)--(2) | / | | / | | / | (3) (4) ''' g2 = Graph(5) g2.graph = [ [0, 1, 0, 1, 0], [1, 0, 1, 1, 1], [0, 1, 0, 0, 1,], [1, 1, 0, 0, 0], [0, 1, 1, 0, 0], ] # Print the solution g2.hamCycle(); # This code is contributed by Divyanshu Mehta> C# // C# program for solution of Hamiltonian // Cycle problem using backtracking using System; public class HamiltonianCycle { readonly int V = 5; int []path; /* A utility function to check if the vertex v can be added at index 'pos'in the Hamiltonian Cycle constructed so far (stored in 'path[]') */ bool isSafe(int v, int [,]graph, int []path, int pos) { /* Check if this vertex is an adjacent vertex of the previously added vertex. */ if (graph[path[pos - 1], v] == 0) return false; /* Check if the vertex has already been included. This step can be optimized by creating an array of size V */ for (int i = 0; i < pos; i++) if (path[i] == v) return false; return true; } /* A recursive utility function to solve hamiltonian cycle problem */ bool hamCycleUtil(int [,]graph, int []path, int pos) { /* base case: If all vertices are included in Hamiltonian Cycle */ if (pos == V) { // And if there is an edge from the last included // vertex to the first vertex if (graph[path[pos - 1],path[0]] == 1) return true; else return false; } // Try different vertices as a next candidate in // Hamiltonian Cycle. We don't try for 0 as we // included 0 as starting point in hamCycle() for (int v = 1; v < V; v++) { /* Check if this vertex can be added to Hamiltonian Cycle */ if (isSafe(v, graph, path, pos)) { path[pos] = v; /* recur to construct rest of the path */ if (hamCycleUtil(graph, path, pos + 1) == true) return true; /* If adding vertex v doesn't lead to a solution, then remove it */ path[pos] = -1; } } /* If no vertex can be added to Hamiltonian Cycle constructed so far, then return false */ return false; } /* This function solves the Hamiltonian Cycle problem using Backtracking. It mainly uses hamCycleUtil() to solve the problem. It returns false if there is no Hamiltonian Cycle possible, otherwise return true and prints the path. Please note that there may be more than one solutions, this function prints one of the feasible solutions. */ int hamCycle(int [,]graph) { path = new int[V]; for (int i = 0; i < V; i++) path[i] = -1; /* Let us put vertex 0 as the first vertex in the path. If there is a Hamiltonian Cycle, then the path can be started from any point of the cycle as the graph is undirected */ path[0] = 0; if (hamCycleUtil(graph, path, 1) == false) { Console.WriteLine('
Solution does not exist'); return 0; } printSolution(path); return 1; } /* A utility function to print solution */ void printSolution(int []path) { Console.WriteLine('Solution Exists: Following' + ' is one Hamiltonian Cycle'); for (int i = 0; i < V; i++) Console.Write(' ' + path[i] + ' '); // Let us print the first vertex again // to show the complete cycle Console.WriteLine(' ' + path[0] + ' '); } // Driver code public static void Main(String []args) { HamiltonianCycle hamiltonian = new HamiltonianCycle(); /* Let us create the following graph (0)--(1)--(2) | / | | / | | / | (3)-------(4) */ int [,]graph1= {{0, 1, 0, 1, 0}, {1, 0, 1, 1, 1}, {0, 1, 0, 0, 1}, {1, 1, 0, 0, 1}, {0, 1, 1, 1, 0}, }; // Print the solution hamiltonian.hamCycle(graph1); /* Let us create the following graph (0)--(1)--(2) | / | | / | | / | (3) (4) */ int [,]graph2 = {{0, 1, 0, 1, 0}, {1, 0, 1, 1, 1}, {0, 1, 0, 0, 1}, {1, 1, 0, 0, 0}, {0, 1, 1, 0, 0}, }; // Print the solution hamiltonian.hamCycle(graph2); } } // This code contributed by Rajput-Ji> Javascript >
PHP // PHP program for solution of // Hamiltonian Cycle problem // using backtracking $V = 5; /* A utility function to check if the vertex v can be added at index 'pos' in the Hamiltonian Cycle constructed so far (stored in 'path[]') */ function isSafe($v, $graph, &$path, $pos) { /* Check if this vertex is an adjacent vertex of the previously added vertex. */ if ($graph[$path[$pos - 1]][$v] == 0) return false; /* Check if the vertex has already been included. This step can be optimized by creating an array of size V */ for ($i = 0; $i < $pos; $i++) if ($path[$i] == $v) return false; return true; } /* A recursive utility function to solve hamiltonian cycle problem */ function hamCycleUtil($graph, &$path, $pos) { global $V; /* base case: If all vertices are included in Hamiltonian Cycle */ if ($pos == $V) { // And if there is an edge from the // last included vertex to the first vertex if ($graph[$path[$pos - 1]][$path[0]] == 1) return true; else return false; } // Try different vertices as a next candidate in // Hamiltonian Cycle. We don't try for 0 as we // included 0 as starting point hamCycle() for ($v = 1; $v < $V; $v++) { /* Check if this vertex can be added to Hamiltonian Cycle */ if (isSafe($v, $graph, $path, $pos)) { $path[$pos] = $v; /* recur to construct rest of the path */ if (hamCycleUtil($graph, $path, $pos + 1) == true) return true; /* If adding vertex v doesn't lead to a solution, then remove it */ $path[$pos] = -1; } } /* If no vertex can be added to Hamiltonian Cycle constructed so far, then return false */ return false; } /* This function solves the Hamiltonian Cycle problem using Backtracking. It mainly uses hamCycleUtil() to solve the problem. It returns false if there is no Hamiltonian Cycle possible, otherwise return true and prints the path. Please note that there may be more than one solutions, this function prints one of the feasible solutions. */ function hamCycle($graph) { global $V; $path = array_fill(0, $V, 0); for ($i = 0; $i < $V; $i++) $path[$i] = -1; /* Let us put vertex 0 as the first vertex in the path. If there is a Hamiltonian Cycle, then the path can be started from any point of the cycle as the graph is undirected */ $path[0] = 0; if (hamCycleUtil($graph, $path, 1) == false) { echo('
Solution does not exist'); return 0; } printSolution($path); return 1; } /* A utility function to print solution */ function printSolution($path) { global $V; echo('Solution Exists: Following is '. 'one Hamiltonian Cycle
'); for ($i = 0; $i < $V; $i++) echo(' '.$path[$i].' '); // Let us print the first vertex again to show the // complete cycle echo(' '.$path[0].'
'); } // Driver Code /* Let us create the following graph (0)--(1)--(2) | / | | / | | / | (3)-------(4) */ $graph1 = array(array(0, 1, 0, 1, 0), array(1, 0, 1, 1, 1), array(0, 1, 0, 0, 1), array(1, 1, 0, 0, 1), array(0, 1, 1, 1, 0), ); // Print the solution hamCycle($graph1); /* Let us create the following graph (0)--(1)--(2) | / | | / | | / | (3) (4) */ $graph2 = array(array(0, 1, 0, 1, 0), array(1, 0, 1, 1, 1), array(0, 1, 0, 0, 1), array(1, 1, 0, 0, 0), array(0, 1, 1, 0, 0)); // Print the solution hamCycle($graph2); // This code is contributed by mits ?>> Izhod
Solution Exists: Following is one Hamiltonian Cycle 0 1 2 4 3 0 Solution does not exist>
Časovna zahtevnost: O(N!), kjer je N število oglišč.
Pomožni prostor: O(1), ker ni uporabljenega dodatnega prostora.
Opomba: Zgornja koda vedno natisne cikel, ki se začne od 0 . Začetna točka ne bi smela biti pomembna, saj je cikel mogoče začeti s katere koli točke. Če želite spremeniti izhodišče, morate narediti dve spremembi zgornje kode.
Spremeni pot[0] = 0; do pot[0] = s ; kje s je tvoja nova Izhodišče . Spremenite tudi zanko za (int v = 1; v