Normalna sila je definirana kot sila, s katero katera koli površina deluje na drug predmet. Ko predmet miruje, je neto sila, ki deluje nanj, enaka nič. Normalne sile ni mogoče uporabiti na dveh površinah, ki med seboj nista povezani. Razlagamo jo lahko kot komponento sile, ki je navpična na katero koli kontaktno površino. Določa, koliko sile telo prenese na tla. Normalna sila je enaka teži predmeta le, če je stopnja spremembe hitrosti predmeta negativna, kar pomeni, da se upočasnjuje.

Formula

Vrednost normalne sile je odvisna od tega, kje je predmet postavljen glede na drugi predmet. Ko bo predmet padel, položaj, v katerem predmet pade na tla, določa vrednost normalne sile. Normalna sila je označena s simbolom F_n. Njegova merska enota je newton (N), dimenzijska formula pa je podana z [M¹L¹T^-2].

Če telo počiva na ploski sili, je normalna sila enaka vrednosti gravitacijske teže, to je mg.

F _n = mg

kje,

F_nje normalna sila,

m je masa mirujočega predmeta,

g je gravitacijski pospešek.

Če telo drsi navzdol s poševne površine pod določenim kotom, je vrednost normalne sile gravitacijska teža, dodana z dodatno silo F sin θ. V tem primeru je normalna sila večja od teže predmeta.

F _n = mg + F sin θ

Kje,

F_nje normalna sila,

m je masa drsnega predmeta,

g je gravitacijski pospešek,

θ je naklonski kot.

Če sila deluje na telo v smeri navzgor, je vrednost normalne sile gravitacijska teža, zmanjšana za silo F sin θ. V tem primeru je neto normalna sila manjša od teže predmeta.

F _n = mg – F sin θ

kje,

vzorčna koda c#

F_nje normalna sila,

m je masa drsnega predmeta,

g je gravitacijski pospešek,

θ je naklonski kot.

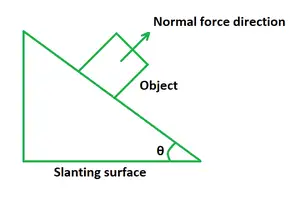
Če telo položimo na nagnjeno ravnino, normalna sila F_nje enak produktu gravitacijske teže in kosinusa naklonskega kota.

F _n = mg cos θ

kje,

F_nje normalna sila,

m je masa drsnega predmeta,

g je gravitacijski pospešek,

θ je naklonski kot.

Vzorčne težave

Naloga 1. Predmet z maso 2 kg leži na mizi. Izračunajte normalno silo, ki deluje nanj.

rešitev:

Imamo,

m = 2

g = 9,8

Z uporabo formule, ki jo dobimo,

F_n= mg

= 2 (9,8)

= 19,6 N

Naloga 2. Predmet leži na mizi s silo 39,2 N. Izračunajte normalno silo, s katero deluje nanj.

rešitev:

Imamo,

F = 39,2

g = 9,8

Z uporabo formule, ki jo dobimo,

F_n= mg

=> m = F/g

=> m = 39,2/9,8

=> m = 4 kg

Naloga 3. Predmet z maso 10 kg s silo 200 N drsi navzdol s poševne površine pod kotom 30°. Izračunajte normalno silo, s katero deluje nanj.

rešitev:

Imamo,

F = 200

m = 10

markdown slike

g = 9,8

θ = 30°

Z uporabo formule, ki jo dobimo,

F_n= mg + F sin θ

= 10 (9,8) + 200 sin 30°

= 98 + 200 (1/2)

= 98 + 100

= 198 N

Naloga 4. Predmet z maso 20 kg s silo 400 N drsi navzdol s poševne površine pod kotom 30°. Izračunajte normalno silo, ki deluje nanj.

rešitev:

Imamo,

F = 400

m = 20

g = 9,8

θ = 30°

Z uporabo formule, ki jo dobimo,

F_n= mg + F sin θ

= 20 (9,8) + 400 brez 30°

= 196 + 400 (1/2)

= 196 + 200

= 396 N

Naloga 5. Predmet z maso 15 kg je postavljen na poševno podlago pod kotom 30°. Izračunajte normalno silo, s katero deluje nanj, če deluje sila navzgor z vrednostjo 100 N.

rešitev:

Imamo,

F = 100

m = 15

g = 9,8

θ = 30°

Z uporabo formule, ki jo dobimo,

F_n= mg – F sin θ

= 15 (9,8) – 100 brez 30°

= 147 – 100 (1/2)

= 147 – 50

= 97 N

Naloga 6. Predmet z maso 5 kg je postavljen na poševno podlago pod kotom 60°. Izračunajte normalno silo, s katero delujete na katero koli točko.

rešitev:

Imamo,

m = 5

g = 9,8

θ = 60°

Z uporabo formule, ki jo dobimo,

F_n= mg cos θ

kartiranje v tipkopisu

= 5 (9,8) (cos 60°)

= 49/2

= 24,5 N

Naloga 7. Predmet je postavljen na poševno površino pod kotom 60°. Izračunajte njegovo maso, če je normalna sila, s katero deluje nanj, 400 N.

rešitev:

Imamo,

F_n= 400,

θ = 60°

Z uporabo formule, ki jo dobimo,

F_n= mg cos θ

m = F/(g cos θ)

= 400/ (9,8 × cos 60°)

= 400/4,9

= 81,63 N