Vztrajnostni moment je lastnost telesa pri rotacijskem gibanju. Vztrajnostni moment je lastnost rotacijskih teles, ki teži k nasprotovanju spremembi rotacijskega gibanja telesa. Podobna je vztrajnosti katerega koli telesa pri translacijskem gibanju. Matematično je vztrajnostni moment podan kot vsota zmnožka mase vsakega delca in kvadrata razdalje od rotacijske osi. Meri se v enoti kgm 2 .
Spoznajmo vztrajnostni moment podrobneje v spodnjem članku.
Kazalo
- Vztrajnostni moment Definicija
- Formula vztrajnostnega momenta
- Dejavniki, ki vplivajo na vztrajnostni moment
- Kako izračunati vztrajnostni moment?
- Formula za vztrajnostni moment za različne oblike
- Polmer vrtenja
- Izreki o vztrajnostnem momentu
- Vztrajnostni momenti za različne predmete
Vztrajnostni moment Opredelitev
Vztrajnostni moment je težnja telesa pri rotacijskem gibanju, ki nasprotuje spremembi njegovega rotacijsko gibanje zaradi zunanjih sil. Vztrajnostni moment se obnaša kot kotna masa in se imenuje rotacijska vztrajnost. Vztrajnostni moment je podoben mehanskemu vztrajnost telesa.
MOI je opredeljen kot količina, izražena z vsoto produkta masa vsakega delca s kvadratom njegove oddaljenosti od osi vrtenja za kateri koli delec, ki izvaja rotacijsko gibanje.
Enota za vztrajnostni moment
Vztrajnostni moment je skalarna količina in enota SI za vztrajnostni moment je kgm 2 .
Dimenzijska formula vztrajnostnega momenta
Ker je vztrajnostni moment podan kot produkt mase in kvadrata razdalje. Njegovo dimenzijska formula je podana z zmnožkom dimenzijske formule mase in kvadrata dimenzijske formule dolžine. Dimenzijska formula vztrajnostnega momenta je, ML 2
Kaj je inercija?
Vztrajnost je lastnost snovi, zaradi katere se upira spremembi stanja svojega gibanja. To pomeni, da telo v mirovanju poskuša ostati v mirovanju in se upreti kakršni koli sili, ki bi ga poskušala premakniti, telo v gibanju pa poskuša nadaljevati gibanje in se upreti kateri koli sili, ki bi ga poskušala spraviti v gibanje, da bi spremenila velikost svojega gibanja. Količinsko je enaka največji sili, ki poskuša spremeniti svoje stanje gibanje .
Izvedite več o vztrajnost .
Formula vztrajnostnega momenta
Vztrajnostni moment je a skalarna količina . Matematično se zmnožek kvadrata mase delca in razdalje od vrtilne osi imenuje vztrajnostni moment delca okoli vrtilne osi.
Splošna formula za iskanje vztrajnostnega momenta katerega koli predmeta je,
jaz = g 2
kje,
m je masa predmeta'
r je razdalja od osi vrtenja
Za telo, sestavljeno iz neprekinjenih infinitezimalno majhnih delcev, se za izračun vztrajnostnega momenta uporablja integralna oblika vztrajnostnega momenta.
I = ∫dI
jaz =
int_{0}^{M} r^2 dm
Vztrajnostni moment sistema delcev
Vztrajnostni moment sistema delcev je podan s formulo,
I = ∑m jaz r jaz 2
kje,
r jaz je pravokotna razdalja ithdelec z osi
m jaz je masa ithdelec
Zgornja enačba vztrajnostnega momenta pove, da je vztrajnostni moment za sistem delcev enak vsoti zmnožka mase vsakega delca in kvadrata razdalje od osi vrtenja vsakega delca.
Za spodnjo sliko,
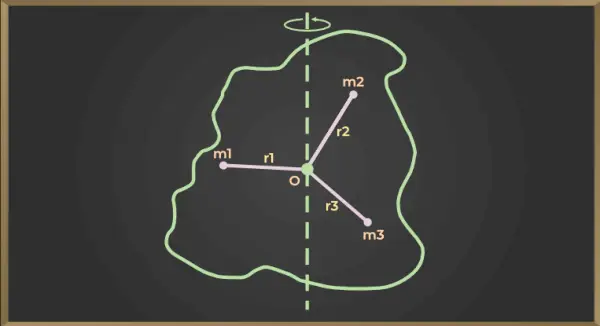
Vztrajnostni moment prvega delca = m1×r12
Vztrajnostni moment drugega delca = m2×r22
Vztrajnostni moment tretjega delca = m3×r32
Podobno,
Vztrajnostni moment nthdelec = mn×rn2
Zdaj vztrajnostni moment celotnega telesa okoli osi vrtenja AB bo enak vsoti vztrajnostnih momentov vseh delcev, torej
jaz = m1×r12+ m2×r22+ m3×r32+……+mn×rn2
matrično množenje v c
I = Σm jaz ×r jaz 2
kje,
jaz predstavljajo vztrajnostni moment telesa okoli vrtilne osi
m jaz je masa ithdelec,
r jaz je polmer ithdelec
S predstavlja vsoto.
Iz enačbe lahko rečemo, da je vztrajnostni moment telesa okoli nepremične osi enak vsoti produkta mase vsakega delca tega telesa in kvadrata njegove pravokotne oddaljenosti od nepremične osi.
Dejavniki, ki vplivajo na vztrajnostni moment
Vztrajnostni moment katerega koli predmeta je odvisen od naslednjih vrednosti:
- Oblika in velikost predmeta
- Gostota materiala predmeta
- Os vrtenja
Kako izračunati vztrajnostni moment?
Uporablja se več načinov izračunajte vztrajnostni moment katerega koli vrtečega se predmeta.
- Pri enotnih predmetih se vztrajnostni moment izračuna tako, da se masa zmnoži s kvadratom njegove oddaljenosti od vrtilne osi (r2).
- Za neenakomerne predmete vztrajnostni moment izračunamo tako, da vzamemo vsoto zmnožka mas posameznih točk pri vsakem različnem polmeru, za to je uporabljena formula
I = ∑m jaz r jaz 2
Formula za vztrajnostni moment za različne oblike
Ta tabela obravnava izraze za vztrajnostni moment za nekatere simetrične predmete skupaj z njihovo osjo vrtenja:

| Objekt | Os | Izraz vztrajnostnega momenta |
|---|---|---|
| Votli valj s tanko steno | Centralno | jaz = g2 |
| Tanek prstan | Premer | jaz = 1/2 g2 |
| Anularni obroč ali votli valj | Centralno | I = 1/2 M(r22+ r12) |
| Trden valj | Centralno | jaz = 1/2 g2 |
| Enotni disk | Premer | jaz = 1/4 g2 |
| Votla krogla | Centralno | jaz = 2/3 g2 |
| Trdna krogla | Centralno | jaz = 2/5 g2 |
| Enotna simetrična sferična lupina | Centralno | |
| Enotna plošča ali pravokotni paralelopiped | Centralno | I = 1/12 M(a2+ b2) |
| Tanka palica | Centralno | jaz = 1/12 g2 |
| Tanka palica | Na koncu Roda | jaz = 1/3 g2 |
Polmer vrtenja
The Polmer vrtenja telesa je definiran kot pravokotna razdalja od osi vrtenja do točke mase, katere masa je enaka masi celotnega telesa, vztrajnostni moment pa je enak dejanskemu vztrajnostnemu momentu predmeta, kot je bil domnevamo, da je tam skoncentrirana celotna masa telesa. To je namišljena razdalja. Polmer vrtenja je označen s K.
Če sta masa in polmer vrtenja telesa M oziroma K, potem je vztrajnostni moment telesa
jaz = MK 2 ……(1)
Tako je polmer vrtenja telesa pravokoten na os vrtenja, katerega kvadrat, pomnožen z maso tega telesa, daje vztrajnostni moment tega telesa okoli te osi.
Spet z enačbo (1), K2= I/M
K = √(I/m)
Tako je polmer vrtenja telesa okoli osi enak kvadratnemu korenu razmerja telesa okoli te osi.
Izreki o vztrajnostnem momentu
Obstajata dve vrsti izrekov, ki sta zelo pomembni glede na vztrajnostni moment:
- Izrek o vzporedni osi
- Izrek o pravokotni osi
Izrek o pravokotni osi
Izrek o pravokotni osi pravi, da je vsota vztrajnostnega momenta telesa okoli dveh medsebojno pravokotnih osi, ki ležita v ravnini telesa, enaka vztrajnostnemu momentu telesa okoli tretje osi, ki je pravokotna na obe osi in poteka skozi njuni točki. križišča.

Na zgornji sliki je OX in LTD sta dve osi v ravnini telesa, ki sta pravokotni druga na drugo. Tretja os je OZ ki je pravokotna na ravnino telesa in poteka skozi presečišče OX in LTD sekire. če jaz x , JAZ in , in jaz z so vztrajnostni momenti telesa okoli osi OX , LTD , in OZ osi, potem po tem izreku
jaz x + jaz in = jaz z
Izrek o vzporedni osi
Po navedbah Izrek o vzporedni osi , je vztrajnostni moment telesa okoli dane osi vsota vztrajnostnega momenta okoli osi, ki poteka skozi masno središče tega telesa, in produkta kvadrata mase telesa in pravokotne razdalje med dve osi.

Naj na zgornji sliki najdemo vztrajnostni moment jaz O telesa, ki gre skozi točko O in okoli osi, pravokotne na ravnino, medtem ko je vztrajnostni moment telesa, ki gre skozi središče mase C in okoli osi, ki je vzporedna z dano osjo, je jaz C , potem v skladu s tem izrekom
jaz O = jaz C + Ml 2
kje
M je masa celotnega telesa
l je pravokotna razdalja med dvema osema.
Vztrajnostni momenti za različne predmete
Vztrajnostni momenti različnih predmetov so obravnavani spodaj v tem članku
Vztrajnostni moment pravokotne plošče
Če je masa plošče M, dolžina l in širina b, potem vztrajnostni moment poteka skozi težišče in okoli osi, pravokotne na ravnino plošče.

I = M(l 2 + b 2 / 12)
Vztrajnostni moment diska
Če ima disk maso M in polmer r, je vztrajnostni moment okoli geometrijske osi diska enak

I = 1/2 (g 2 )
Vztrajnostni moment palice
Če je masa palice M in dolžina l, potem vztrajnostni moment okoli osi, ki je pravokotna na dolžino palice in poteka skozi njeno težišče
poskusite strukturo podatkov

jaz = ML 2 /12
Vztrajnostni moment kroga
Če je masa obroča M in polmer obroča r, potem je vztrajnostni moment okoli osi, ki poteka skozi pravokotno na središče obroča

jaz = g 2
Vztrajnostni moment krogle
Če ima trdna krogla maso M in polmer r, potem je vztrajnostni moment okoli njenega premera enak

I = 2/5 Mr 2
Vztrajnostni moment polnega valja
Vztrajnostni moment polnega valja s polmerom 'R' in maso M je podan z

I = 1/2MR 2
Vztrajnostni moment votlega valja
Votel valj ima dva polmera, in sicer notranji polmer in zunanji polmer. Vztrajnostni moment votlega valja z maso M, zunanjim polmerom R1, in notranji polmer R2je podan kot

I = 1/2M(R 1 2 + R 2 2 )
Vztrajnostni moment trdne krogle
Vztrajnostni moment trdne krogle z maso 'M' in polmerom 'R' je podan kot

I = 2/5MR 2
Vztrajnostni moment votle krogle
Vztrajnostni moment votle krogle z maso M in polmerom 'R' je podan kot

I = 2/3MR 2
Vztrajnostni moment obroča
Vztrajnostni moment obroča je podan za dva primera, ko gre vrtilna os skozi središče in ko gre vrtilna os skozi premer.
Vztrajnostni moment obroča okoli osi, ki poteka skozi središče, je podan z
pretvori niz v int

jaz = GOSPOD 2
Vztrajnostni moment obroča okoli osi, ki poteka skozi premer, je podan z

jaz = g 2 /2
Vztrajnostni moment kvadrata
Vztrajnostni moment kvadrata stranice 'a' je podan kot

jaz = a 4 /12
Vztrajnostni moment kvadratne plošče s stranico dolžine 'l' in maso M je podan kot
I = 1/6ML 2
Vztrajnostni moment trikotnika
Vztrajnostni moment trikotnika je podan za 3 situacije, prvič, ko gre os skozi središče, drugič, ko gre os skozi osnovo in tretjo, ko je os pravokotna na osnovo. Oglejmo si formulo zanje enega za drugim. Za trikotnik z osnovo 'b' in višino 'h' je formula za vztrajnostni moment podana takole

Ko gre os skozi Centroid
jaz = bh 3 /36
Ko gre os skozi bazo
jaz = bh 3 /12
Ko je os pravokotna na osnovo
I = (hb/36)(b 2 – b 1 b + b 1 2 )
Razlika med vztrajnostnim momentom in vztrajnostjo
Razlika med vztrajnostjo in vztrajnostnim momentom je prikazana v spodnji tabeli:
| da ne | vztrajnost | Vztrajnostni moment |
|---|---|---|
| 1. | Njegov pomen je v linearnem gibanju. | Njegov pomen je v rotacijskem gibanju. |
| 2. | Je tista lastnost predmeta, ki nasprotuje spremembi stanja predmeta pri linearnem gibanju. | Vztrajnostni moment je tista lastnost predmeta, ki nasprotuje spremembi stanja predmeta pri rotacijskem gibanju. |
| 3. | Vztrajnost predmeta je odvisna le od njegove mase. | Vztrajnostni moment predmeta je odvisen od njegove mase in porazdelitve mase glede na vrtilno os. |
| 4. | Vztrajnost predmeta je fiksna. | Vztrajnostni moment predmeta se spreminja glede na različne osi vrtenja. |
Kinetična energija rotacijskega telesa
Predpostavimo, da se telo z maso 'm' vrti s hitrostjo v na razdalji 'r' od osi vrtenja. Njegova kotna hitrost je nato podana z ω = v/r in nato v = rω. Zdaj vemo, da je Kinetična energija telesa daje
KE = 1/2mv 2
⇒ KE = 1/2m(rω)2
⇒ KE = 1/2mr2oh2
⇒ KE = 1/2Iω 2
Zato je kinetična energija rotirajočega telesa podana s polovico produkta vztrajnostnega momenta in kotna hitrost telesa. Imenuje se tudi kinetična energija vrtečega se telesa Rotacijska kinetična energija . Formula rotacijske kinetične energije je podana kot
KE = 1/2Iω 2
Vztrajnostni moment (I) je neodvisen od kotne hitrosti telesa. Je funkcija mase rotirajočega telesa in oddaljenosti telesa od osi vrtenja. Zato opazimo, da je kotno gibanje analogno linearnemu gibanju, kar pomeni, da je pomen vztrajnostnega momenta v tem, da daje predstavo o tem, kako so mase porazdeljene na različne razdalje od osi vrtenja v rotirajočem telesu.
Uporaba vztrajnostnega momenta
Vztrajnostni moment ima različne aplikacije, od katerih so nekatere obravnavane spodaj:
- Zaradi večjega vztrajnostnega momenta se zemlja vrti okoli svoje osi z enako kotno hitrostjo.
- Pod otroški igralni motor je nameščeno majhno gibljivo kolo. Ko to kolo podrgnete s tlemi in zapustite motor, zaradi vztrajnostnega momenta kolesa motor še nekaj časa deluje.
- Vsak motor je sestavljen iz velikega in težkega kolesa, pritrjenega na njegovo gred, pri čemer je večina njegove mase na njegovem obodu. Zato je njegov vztrajnostni moment visok. To kolo se imenuje vztrajnik. Navor, ki poganja gred motorja, se povečuje. Zato vrtenje gredi morda ni enakomerno, toda zaradi prisotnosti gibajočega se kolesa z večjo vztrajnostjo se gred še naprej vrti s skoraj enakomerno hitrostjo.
- V kolesu volovskih vpreg, rikš, skuterjev, koles itd. je večina mase skoncentrirana na njegovem krogu ali platišču. ta obroč ali rutina je pritrjena na os kolesa s togimi naperami. S tem se njegov vztrajnostni moment poveča. Ko se torej med kolesarjenjem noge nehajo premikati, se kolo še nekaj časa vrti.
Prav tako preverite
- Kinematika rotacijskega gibanja
- Gibanje togega telesa
- Kotalno gibanje
Rešeni primeri o vztrajnostnih momentih
Primer 1: Telo z maso 500 g se vrti okoli osi. oddaljenost težišča mase telesa od vrtilne osi je 1,2 m. poiščite vztrajnostni moment telesa okoli osi vrtenja.
rešitev:
Če upoštevamo, da je M = 500 g = 0,5 kg, je r = 1,2 m.
Očitno lahko predpostavimo, da je celotna masa telesa postavljena v njegovo središče mase. Nato vztrajnostni moment telesa okoli osi vrtenja.
jaz = g2
I = 0,5 × (1,2)2
I = 0,72 kg m2
Primer 2: Vrtilni polmer okoli osi, ki je 12 cm oddaljena od središča mase telesa z maso 1,2 kg, je 13 cm. Izračunajte vrtilni polmer in vztrajnostni moment okoli osi, ki poteka skozi središče mase.
rešitev:
Če upoštevamo, da je M = 1,0 kg, K = 13 cm, l = 12 cm, KCM= ?, jazCM= ?
Iz izreka o vzporedni osi I = ICM+ Ml2
K2= KCM2+ l2
ali KCM2= K2– l2
KCM2 = (13)2– (12)2= 25
java if izjavaKCM= 5
Zdaj vztrajnostni moment ICM= MKCM2
jazCM= 1,0 × (0,05)2= 2,5 × 10-3kg m2
Primer 3: Telo z maso 0,1 kg se vrti okoli osi. če je oddaljenost središča mase telesa od osi vrtenja 0,5 m, potem poiščite vztrajnostni moment telesa.
rešitev:
Glede na to je M = 0,1 kg in r = 0,5 m
torej jaz = g2
I = 0,1 × (0,5)2
I = 0,025 kg m2
Primer 4: Vztrajnostni moment obročev okoli osi, ki poteka skozi središče pravokotno na ravnino krožnega obroča, je 200 gm cm 2 . Kolikšen bo vztrajnostni moment glede na njegov premer?
rešitev:
Vztrajnostni moment krožnega obroča okoli osi, ki poteka skozi drugo središče pravokotno na njegovo ravnino
GOSPOD2= 200 gm cm2
Vztrajnostni moment okoli premera
= 1/2 MR2
= 1/2 × 200 = 100 gm cm2
Pogosta vprašanja o vztrajnostnih momentih
Kako izračunati vztrajnostni moment?
Osnovna formula za iskanje vztrajnostnega momenta katerega koli enakomernega predmeta je,
jaz = g 2
kje,
m je masa predmeta'
r je razdalja od osi vrtenja
Kako izračunati vztrajnostni moment žarka?
Vztrajnostni moment nosilca vzdolž središča in osi, ki je vodoravna nanj, se izračuna po formuli,
jaz = ML 2 / 12
Od česa je odvisen vztrajnostni moment telesa?
Vztrajnostni moment katerega koli predmeta je odvisen od spodaj navedenih dejavnikov:
- Masa telesa,
- Os vrtenja
- Oblika in velikost predmeta
Kaj je enota za vztrajnostni moment?
Enota za vztrajnostni moment je Kgm 2
Ali je lahko vztrajnostni moment negativen?
Ne, vztrajnostni moment nikoli ne more biti negativen.
Kaj je masni vztrajnostni moment?
Masni vztrajnostni moment je meritev odpornosti telesa na spremembo njegovega kotnega momenta ali smeri. Masni vztrajnostni moment za maso točke je podan z I = mr2in za sistem delcev je vztrajnostni moment mase podan kot I = Σjazmjazrjaz2
Kaj je vztrajnostni moment območja?
Območni vztrajnostni moment je lastnost ravnine 2D oblike, ki prikazuje, kako so točke razpršene glede na poljubno os v ravnini. Površinski vztrajnostni moment je znan tudi kot drugi ploščinski moment ali kvadratni ploščinski moment. Formula za vztrajnostni moment površine v ravnini xy je podana kot Ixy= ∫xy dxdxy = ∫xy dA
