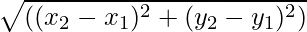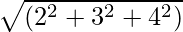logo

TechCodeview

Magnituda vektorja

Vektorske količine so količine, ki imajo tako smer kot velikost. Velikost vektorja je dolžina vektorja. Podana je s številsko vrednostjo vektorja in ker predstavlja dolžino vektorja, je vedno pozitivna. Za kateri koli vektor 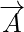overrightarrow{A}njegova velikost je predstavljena kot overrightarrow{A}.

V tem članku izvemo več o velikosti vektorja, njegovi formuli, primerih in drugem.



Kazalo

Kakšna je velikost vektorja?

Magnituda vektorja je definirana kot dolžina vektorja. Ker velikost vektorja označuje dolžino vektorja, je vedno pozitivna. Za vsak vektor A je njegova velikost predstavljena kot |A|. Recimo, da je vektor definiran kot xi + yj, potem je njegova velikost definirana kot kvadratni koren vsote kvadratov posameznih členov. Velikost vektorja predstavlja dolžino vektorja, tj. vrednost ali vpliv, ki ga ima vektor.

Na primer, če na predmet deluje sila 5i N, potem je njena velikost 5 N, kar pomeni, da je moč uporabljene sile 5 N in ' jaz' v 5i predstavlja, da se uporablja v pozitivni smeri x.



Magnituda vektorske formule

Obstajajo različni načini za izračun velikosti vektorja. Na podlagi danih podatkov uporabite drugo vrsto formule za iskanje velikosti vektorja. Velikost vektorja A je predstavljena z uporabo operatorja modula, tj. |A|

Obstajajo različne formule, ki se uporabljajo za štetje velikosti vektorja. Naslednja slika prikazuje pomembne formule, ki se uporabljajo za iskanje velikosti vektorja.

Magnituda vektorske formule

Sledijo načini za izračun velikosti.



  • Če jim je dan vektor Ā = xi+ yĵ + zk̂, potem lahko velikost vektorja Ā izračunate s spodnjo formulo

Magnituda vektorja Ā (|A|) = √(x 2 + in 2 +z 2 )

  • Če je vektor začetne točke recimo (x1, in1) in končna točka vektorja je recimo (x2, in2) sta podana velikost vektorja addesna puščica{AB}daje,
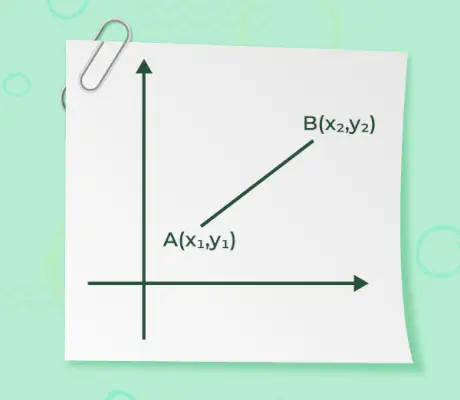
Magnituda vektorja, če sta podani dve točki

Velikost vektorja, ko sta podani začetna in končna točka vektorja, ni nič drugega kot razdalja med točkama. Formula za iskanje velikosti je podana z

addesna puščica{AB}= sqrt{((x_2-x_1)^2+(y_2-y_1)^2)}

  • Če je katera koli začetna ali končna točka vektorja v izhodišču o(0, 0) in je druga točka A(x, y) kot je navedeno na spodnji sliki,
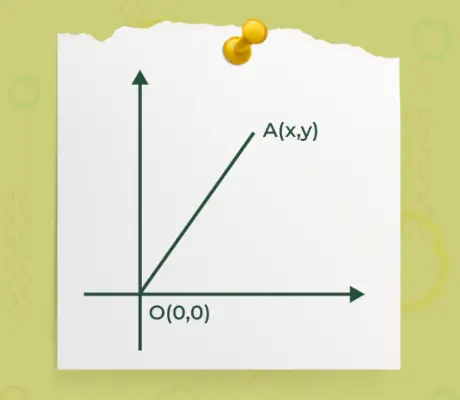
Magnituda vektorja, če sta podana ena točka in izhodišče

Potem je formula za iskanje velikosti vektorja, kjer je eden od koncev vektorja v izhodišču, podana z

|Ā| = √(x 2 +y 2 )

Smer vektorja

Vektorske količine so količine, ki imajo tako velikosti kot smeri. Smer vektorske količine označuje, v katero smer se uporablja vektorska količina. Definiran je kot kot, ki ga vektor tvori z vodoravno črto ali osjo x. Predstavljen je s simbolom a .

Spodnja slika prikazuje puščico, ki se uporablja za prikaz smeri vektorja.

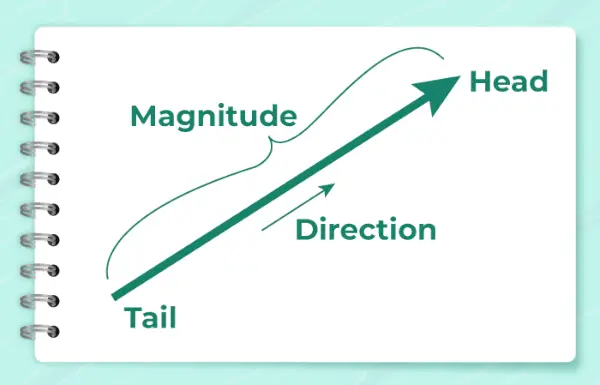
Smer vektorja

Izračuna se po formuli,

α = tan -1 (l/x)

java odprta datoteka

Za vektor, ki ga ustvarijo koordinate (x1, in1) in (x2, in2) njihova smer je podana s formulo,

α = tan -1 [(in 2 - in 1 )/(x 2 – x 1 )]

Kako najti velikost vektorja?

Velikost vektorja se izračuna z uporabo spodaj opisanih korakov,

Korak 1: Določite komponente x, y in z vektorja.

2. korak : Poiščite kvadrat vseh komponent x, y in z.

3. korak: Dodajte vse kvadrate, ki jih najdete v 2. koraku.

4. korak: Poiščite kvadratni koren vsote, dobljene v 3. koraku.

Vrednost, dobljena po koraku 4, je velikost danega vektorja.

Primer: Poiščite velikost vektorja A = 3i + 4j

format niza v Javi

rešitev:

Velikost vektorja A se izračuna z uporabo zgoraj opisanih korakov.

Korak 1: Če primerjamo A = 3i + 4j s xi + yj, dobimo x = 3 in y = 4

2. korak: x2= 32= 9 in y2= 42= 16

3. korak: x2+ in2= 9 + 16 = 25

4. korak: √(25) = 5

Tako je velikost vektorja A = 3i + 4j 5 enot.

Zaključek

Skratka, velikost vektorja nam pove, kako dolg je vektor. Ta koncept je zelo pomemben na številnih področjih, kot so fizika, inženiring in računalništvo, saj pomaga meriti stvari, kot so hitrost, sila in smer gibanja. Z razumevanjem vektorske velikosti lahko bolje analiziramo in rešujemo praktične probleme, zaradi česar je ključno znanje za vse, ki delajo s števili in meritvami v aplikacijah v resničnem svetu.

Preberi več,

Rešeni primeri o velikosti vektorja

Primer 1: Poiščite velikost vektorja Ā = 2i + 3ĵ + 4k.

rešitev:

primerljiv seznam

podano,

Ā = 2i + 3ĵ + 4k

Magnituda |A| = sqrt{(2^2+3^2+4^2)}

= sqrt{(4+9+16)}
= √29
= 5,38

Velikost vektorja 2i+3ĵ+4k je 5.38 enota

Primer 2: Poiščite velikost za vektor Ā = 3i + 3ĵ – 6k

rešitev:

dano

Ā = 3i + 3ĵ – 6k

Magnituda |A| = sqrt{(3^2+3^2+(-6)^2)}

= sqrt{(9+9+36)}
= √54
= 7,35

Velikost vektorja 3i+ 3ĵ – 6k je 7.35 enota.

Primer 3: Poiščite velikost vektorja, če je začetna točka vektorja (3, 4) in končna točka (6, 2).

rešitev:

podano,

(x1, in1) = (3, 4)
(x2, in2) = (6, 2)

|Ā|= sqrt{((x_2-x_1)^2+(y_2-y_1)^2)}

= sqrt{((6-3)^2+(2-4)^2)}
= √(32+ (-2)2)
= √(9+4)
= √13 = 3,6

Tako je velikost danega vektorja 3.6 enota.

Primer 4: Poiščite velikost vektorja, če je začetna točka vektorja (2, 1, 4) in končna točka (5, 2, 6).

rešitev:

podano,

(x1, in1, z1) = (2, 1, 4)

(x2, in2, z2) = (5, 2, 6)

|Ā| = sqrt{((x_2-x_1)^2+(y_2-y_1)^2)}

= sqrt{((5-2)^2+(2-1)^2+(6-4)^2)}
= sqrt{(32+12+22)}
= √(9 +1 + 4)
= √14 = 3,74

Tako je velikost danega vektorja 3.74 enota.

Primer 5: Kakšna je velikost vektorja, ki se začne na začetku in konča na (3, 4).

rešitev:

podano,

Začetna točka vektorja je O(0, 0)

jquery ta klik

Končna točka (x, y) = (3, 4)

Magnituda vektorja (|Ā|) = √(x2+y2)

= √(32+ 42)
= √(9 + 16)
= √25 = 5

Tako je velikost danega vektorja 5 enota.

Primer 6: Poiščite velikost vektorja, v katerem je ena od končnih točk v izhodišču, druga pa v (1, 4, 3).

rešitev:

podano,

Končna točka vektorja je O(0, 0)

Druga točka (x, y, z) = (1, 4, 3)

Magnituda vektorja (|Ā|) = √(x2+y2+z2)

= sqrt{(1^2+4^2+3^2)}
= sqrt{(1+16+9)}
= √26 = 5,09

Tako je velikost danega vektorja 5.09 enota.

kako preimenovati imenik linux

Pogosta vprašanja o velikosti vektorja

Kakšna je velikost vektorske formule?

Velikost vektorja je številska vrednost vektorja in določa dolžino vektorja. Za vsak vektor A je njegova velikost predstavljena kot |A|. Velikost vektorja se izračuna po formuli,

Za kateri koli vektor A = xi + yj + zk je njegova velikost podana s formulo

|A| = √(x 2 + in 2 + z 2 )

Za vsak vektor, katerega začetna in končna točka sta (x1, in1) in (x2, in2) je njegova velikost podana s formulo

|A| = √((x 2 – x 1 ) 2 + (in 2 - in 1 ) 2 )

Kako predstaviti velikost vektorja?

Velikost vektorja A je predstavljen s simbolom |A|.

Kako najti velikost vektorja?

Za izračun velikosti vektorja se uporabljajo različne formule, nekatere od njih so,

  • |A| = √(x 2 + in 2 + z 2 ) ko je vektor v obliki A = xi + yj + zk
  • |A| = √((x) 2 + (in) 2 ) ko je vektor podan s točko A (x, y) in izhodiščem O(0, 0).
  • |A| = √((x 2 – x 1 ) 2 + (in 2 - in 1 ) 2 ) ko je vektor podan s točko A (x1, in2) in točka B (x2, in2).

Poiščite vektor magnitude 5.

Obstajajo različni vektorji, ki imajo lahko magnitudo 5, primer tega je vektor A, predstavljen kot

A = 3i + 4j ali A = 4i + 5j