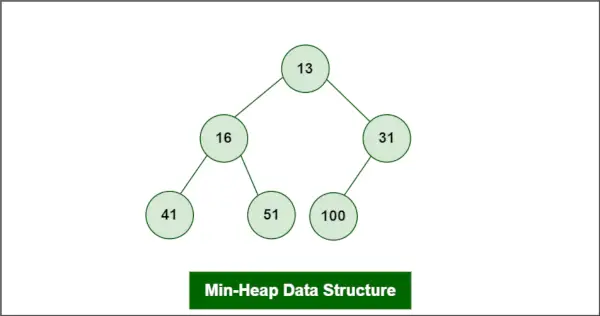
A Min-kup je opredeljena kot vrsta Podatkovna struktura kopice je vrsta binarnega drevesa, ki se običajno uporablja v računalništvu za različne namene, vključno z razvrščanjem, iskanjem in organiziranjem podatkov.
Uvod v Min-Heap – Vadnice za strukturo podatkov in algoritme
Namen in primeri uporabe Min-Heap:
- Implementacija prednostne čakalne vrste: Ena od primarnih uporab podatkovne strukture kopice je za izvajanje prednostnih čakalnih vrst.
- Dijkstrajev algoritem : Dijkstrajev algoritem je algoritem najkrajše poti, ki najde najkrajšo pot med dvema vozliščema v grafu. Min kopico lahko uporabite za spremljanje neobiskanih vozlišč z najmanjšo razdaljo od izvornega vozlišča.
- Razvrščanje: Najmanjšo kopico lahko uporabite kot algoritem za razvrščanje za učinkovito razvrščanje zbirke elementov v naraščajočem vrstnem redu.
- Mediana ugotovitev: Min kopico lahko uporabite za učinkovito iskanje mediane toka števil. Uporabimo lahko en min heap za shranjevanje večje polovice števil in en max heap za shranjevanje manjše polovice. Mediana bo koren min heapa.
Struktura podatkov Min-Heap v različnih jezikih:
1. Min-Heap v C++
Min kopico je mogoče implementirati z uporabo prednostna_čakalna vrsta vsebnik iz knjižnice standardnih predlog (STL). The prednostna_čakalna vrsta kontejner je vrsta vsebniškega adapterja, ki omogoča shranjevanje elementov v čakalni vrsti podobni podatkovni strukturi, v kateri ima vsak element prednost, povezano z njim.
Sintaksa :
C++ priority_queue < int, vector , večji > minH;>
2. Min-Heap v Javi
V Javi je mogoče minimalno kopico implementirati z uporabo PriorityQueue razred od paket java.util . Razred PriorityQueue je prednostna čakalna vrsta, ki zagotavlja način za shranjevanje elementov v čakalni vrsti podobni podatkovni strukturi, v kateri ima vsak element z njim povezano prioriteto.
Sintaksa :
Java PriorityQueue minHeap = nova PriorityQueue ();>
3. Min-Heap v Pythonu
V Pythonu je mogoče minimalno kopico implementirati z uporabo heapq modul, ki nudi funkcije za izvajanje kopic. Natančneje, heapq modul ponuja način za ustvarjanje in upravljanje podatkovnih struktur kopice.
Sintaksa:
Python heap = [] heapify(heap)>
4. Min-Heap v C#
V C# je mogoče minimalno kopico implementirati z uporabo razreda PriorityQueue iz System.Collections.Generic imenski prostor . Razred PriorityQueue je prednostna čakalna vrsta, ki zagotavlja način za shranjevanje elementov v čakalni vrsti podobni podatkovni strukturi, v kateri ima vsak element z njim povezano prioriteto.
programski vzorci java
Sintaksa:
C# var minHeap = new PriorityQueue ();>
5. Min-heap v JavaScriptu
Najmanjša kopica je binarno drevo, kjer ima vsako vozlišče vrednost, ki je manjša ali enaka svojim otrokom. V JavaScriptu lahko implementirate najmanjšo kopico z uporabo matrike, kjer prvi element predstavlja korensko vozlišče, otroci vozlišča pa indeks jaz se nahajajo na indeksih 2i+1 in 2i+2.
Sintaksa:
JavaScript const minHeap = new MinHeap();>
Razlika med Min Heap in Max Heap:
|
| Najmanjša kopica | Max Heap |
|---|---|---|
| 1. | V Min-Heap mora biti ključ, ki je prisoten v korenskem vozlišču, manjši ali enak med ključi, ki so prisotni pri vseh njegovih podrejenih elementih. | V Max-Heap mora biti ključ, ki je prisoten v korenskem vozlišču, večji ali enak med ključi, ki so prisotni pri vseh njegovih podrejenih. |
| 2. | V Min-Heap je minimalni ključni element prisoten v korenu. | V največji kopici je največji ključni element prisoten v korenu. |
| 3. | Min-Heap uporablja naraščajočo prioriteto. | Max-Heap uporablja padajočo prioriteto. teorija dreves in grafov |
| 4. | Pri konstrukciji Min-Heap ima prednost najmanjši element. pretvorba niza v int v Javi | Pri konstrukciji Max-Heap ima prednost največji element. |
| 5. | V Min-Heap-u je najmanjši element prvi, ki se odstrani iz kupa. | V največji kopici je največji element prvi, ki se odstrani iz kopice. |
Notranja izvedba podatkovne strukture Min-Heap:
A Najmanjša kopica je običajno predstavljena kot niz .
- Korenski element bo pri Prihod[0] .
- Za katero koli ith vozlišče Prihod[i] :
- Arr[(i -1) / 2] vrne svoje nadrejeno vozlišče.
- Arr[(2 * i) + 1] vrne svoje levo podrejeno vozlišče.
- Arr[(2 * i) + 2] vrne svoje desno podrejeno vozlišče.
Notranja implementacija Min-Heap zahteva 3 glavne korake:
- Vstavljanje : Za vstavljanje elementa v najmanjšo kopico najprej dodamo element na konec matrike in nato prilagodimo lastnost kopice tako, da večkrat zamenjamo element z njegovim nadrejenim elementom, dokler ni v pravilnem položaju.
- Izbris : Če želite odstraniti minimalni element iz najmanjše kopice, najprej zamenjamo korensko vozlišče z zadnjim elementom v matriki, odstranimo zadnji element in nato prilagodimo lastnost kopice tako, da večkrat zamenjamo element z najmanjšim podrejenim elementom, dokler ni v pravilen položaj.
- Heapify : Operacijo heapify lahko uporabite za ustvarjanje najmanjše kopice iz nerazvrščene matrike.
Operacije na strukturi podatkov Min-heap in njihova implementacija:
Tukaj je nekaj običajnih operacij, ki jih je mogoče izvesti na podatkovni strukturi kopice,
1. Vstavljanje v strukturo podatkov Min-Heap :
Elemente je mogoče vstaviti v kopico po podobnem pristopu, kot je opisano zgoraj za brisanje. Ideja je:
- Operacija vstavljanja v najmanjšo kopico vključuje naslednje korake:
- Dodajte nov element na konec kopice, na naslednji razpoložljivi položaj v zadnji ravni drevesa.
- Primerjajte nov element z njegovim staršem. Če je nadrejeni element večji od novega elementa, ju zamenjajte.
- Ponavljajte korak 2, dokler nadrejeni element ni manjši ali enak novemu elementu ali dokler novi element ne doseže korena drevesa.
- Novi element je zdaj v pravilnem položaju v kopici min in lastnost kopice je izpolnjena.
Ilustracija:
Recimo, da je kopica najmanjša kopica kot:
Vstavljanje v Min-Heap
Implementacija operacije vstavljanja v Min-Heap:
C++ #include #include using namespace std; // Function to insert a new element into the min-heap void insert_min_heap(vector & heap, int value) { // Dodaj nov element na konec kopice heap.push_back(value); // Pridobi indeks zadnjega elementa int index = heap.size() - 1; // Primerjaj nov element z njegovim nadrejenim in // po potrebi zamenjaj while (index> 0 && heap[(index - 1) / 2]> heap[index]) { swap(heap[index], heap[(index - 1) / 2]); // Premakni se po drevesu navzgor do nadrejenega // elementa index = (index - 1) / 2; } } // Glavna funkcija za preizkus funkcije insert_min_heap int main() { vektor kup; int vrednosti [] = { 10, 7, 11, 5, 4, 13 }; int n = sizeof(vrednosti) / sizeof(vrednosti[0]); za (int i = 0; i< n; i++) { insert_min_heap(heap, values[i]); cout << 'Inserted ' << values[i] << ' into the min-heap: '; for (int j = 0; j < heap.size(); j++) { cout << heap[j] << ' '; } cout << endl; } return 0; }>
Java import java.util.*; public class GFG { // Function to insert a new element into the min-heap public static void insertMinHeap(int[] heap, int size, int value) { // Add the new element to the end of the heap heap[size] = value; // Get the index of the last element int index = size; // Compare the new element with its parent and swap // if necessary while (index>0 && kopica[(indeks - 1) / 2]> kopica[indeks]) { zamenjaj(kupica, indeks, (indeks - 1) / 2); // Premakni se po drevesu navzgor do nadrejenega // elementa index = (index - 1) / 2; } } // Funkcija za zamenjavo dveh elementov v matriki public static void swap(int[] arr, int i, int j) { int temp = arr[i]; arr[i] = arr[j]; arr[j] = temp; } // Glavna funkcija za preizkus funkcije insertMinHeap public static void main(String[] args) { int[] heap = new int[6]; int[] vrednosti = { 10, 7, 11, 5, 4, 13 }; int velikost = 0; za (int i = 0; i< values.length; i++) { insertMinHeap(heap, size, values[i]); size++; System.out.print('Inserted ' + values[i] + ' into the min-heap: '); for (int j = 0; j < size; j++) { System.out.print(heap[j] + ' '); } System.out.println(); } } }> Python3 def insert_min_heap(heap, value): # Add the new element to the end of the heap heap.append(value) # Get the index of the last element index = len(heap) - 1 # Compare the new element with its parent and swap if necessary while index>0 in kopica[(indeks - 1) // 2]> kopica[indeks]: kopica[indeks], kopica[(indeks - 1) // 2] = kopica[(indeks - 1) // 2], kopica[ index] # Premakni drevo navzgor do nadrejenega elementa index = (index - 1) // 2 heap = [] values = [10, 7, 11, 5, 4, 13] for value in values: insert_min_heap( kopica, vrednost) print(f'Vstavljena {vrednost} v najmanjšo kopico: {kopica}')> C# using System; using System.Collections.Generic; public class Program { // Function to insert a new element into the min-heap static void InsertMinHeap(List heap, int value) { // Dodajte nov element na konec kopice heap.Add(value); // Pridobi indeks zadnjega elementa int index = heap.Count - 1; // Primerjaj nov element z njegovim nadrejenim in // po potrebi zamenjaj while (index> 0 && heap[(index - 1) / 2]> heap[index]) { int temp = heap[index]; kopica[indeks] = kopica[(indeks - 1) / 2]; kopica [(indeks - 1) / 2] = temp; // Premakni se po drevesu navzgor do nadrejenega // elementa index = (index - 1) / 2; } } // Glavna funkcija za preizkus funkcije InsertMinHeap public static void Main() { List kopica = nov seznam (); int[] vrednosti = { 10, 7, 11, 5, 4, 13 }; foreach(int vrednost v vrednostih) { InsertMinHeap(kup, vrednost); Console.Write('Vstavljeno ' + vrednost + ' v najmanjšo kopico: '); foreach(int element v kopici) { Console.Write(element + ' '); } Console.WriteLine(); } } }> Javascript function insertMinHeap(heap, value) { heap.push(value); let index = heap.length - 1; let parentIndex = Math.floor((index - 1) / 2); while (index>0 && heap[parentIndex]> heap[index]) { [heap[indeks], heap[parentIndex]] = [heap[parentIndex], heap[index]]; indeks = parentIndex; parentIndex = Math.floor((indeks - 1) / 2); } } // Primer uporabe const heap = []; vrednosti const = [10, 7, 11, 5, 4, 13]; za (konstantna vrednost vrednosti) { insertMinHeap(kup, vrednost); console.log(`Vstavljeno ${value} v min-heap: ${heap}`); }> Izhod
Inserted 10 into the min-heap: 10 Inserted 7 into the min-heap: 7 10 Inserted 11 into the min-heap: 7 10 11 Inserted 5 into the min-heap: 5 7 11 10 Inserted 4 into the min-heap: 4 5 11 10 7 Inser...>
Časovna kompleksnost: O(log(n)) ( kjer je n št elementov v kupu )
Pomožni prostor: O(n)
2. Izbris v strukturi podatkov Min-Heap :
Odstranitev najmanjšega elementa (korena) iz kopice min. Koren se nadomesti z zadnjim elementom v kopici, nato pa se lastnost kopice obnovi z zamenjavo novega korena z njegovim najmanjšim otrokom, dokler nadrejeni ni manjši od obeh otrok ali dokler nov koren ne doseže listnega vozlišča.
- Zamenjajte koren ali element, ki ga želite izbrisati, z zadnjim elementom.
- Izbrišite zadnji element iz kopice.
- Ker je zadnji element zdaj postavljen na položaj korenskega vozlišča. Torej morda ne sledi lastnosti kopice. Zato kopičite zadnje vozlišče na mestu korena.
Ilustracija :
Recimo, da je kopica najmanjša kopica kot:
Podatkovna struktura minimalne kopice
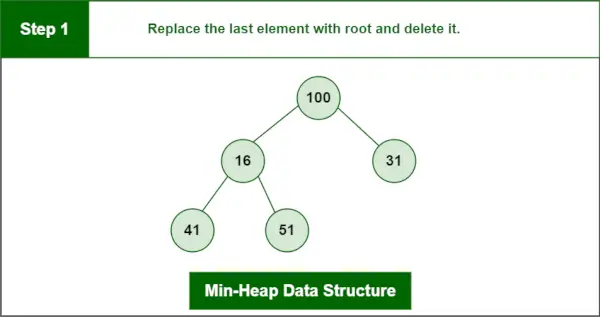
Element, ki ga želite izbrisati, je root, tj. 13.
Proces :
Zadnji element je 100.
Korak 1: Zadnji element zamenjajte s root in ga izbrišite.
Podatkovna struktura minimalne kopice
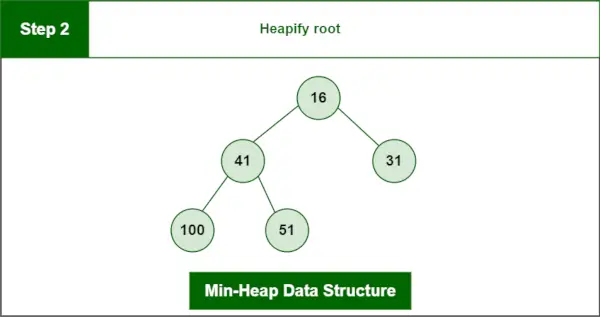
2. korak : Heapify root.
čakalna vrsta v JaviKončna kopica:
Podatkovna struktura minimalne kopice
Izvedba operacije brisanja v Min-Heap:
C++ #include #include using namespace std; // Function to insert a new element into the min-heap void insert_min_heap(vector & heap, int value) { // Dodaj nov element na konec kopice heap.push_back(value); // Pridobi indeks zadnjega elementa int index = heap.size() - 1; // Primerjaj nov element z njegovim nadrejenim in // po potrebi zamenjaj while (index> 0 && heap[(index - 1) / 2]> heap[index]) { swap(heap[index], heap[(index - 1) / 2]); // Premakni se po drevesu navzgor do nadrejenega // elementa index = (index - 1) / 2; } } // Funkcija za brisanje vozlišča iz najmanjše kopice void delete_min_heap(vektor & heap, int value) { // Poiščite indeks elementa, ki ga želite izbrisati int index = -1; za (int i = 0; i< heap.size(); i++) { if (heap[i] == value) { index = i; break; } } // If the element is not found, return if (index == -1) { return; } // Replace the element to be deleted with the last // element heap[index] = heap[heap.size() - 1]; // Remove the last element heap.pop_back(); // Heapify the tree starting from the element at the // deleted index while (true) { int left_child = 2 * index + 1; int right_child = 2 * index + 2; int smallest = index; if (left_child < heap.size() && heap[left_child] < heap[smallest]) { smallest = left_child; } if (right_child < heap.size() && heap[right_child] < heap[smallest]) { smallest = right_child; } if (smallest != index) { swap(heap[index], heap[smallest]); index = smallest; } else { break; } } } // Main function to test the insert_min_heap and // delete_min_heap functions int main() { vector kup; int vrednosti [] = { 13, 16, 31, 41, 51, 100 }; int n = sizeof(vrednosti) / sizeof(vrednosti[0]); za (int i = 0; i< n; i++) { insert_min_heap(heap, values[i]); } cout << 'Initial heap: '; for (int j = 0; j < heap.size(); j++) { cout << heap[j] << ' '; } cout << endl; delete_min_heap(heap, 13); cout << 'Heap after deleting 13: '; for (int j = 0; j < heap.size(); j++) { cout << heap[j] << ' '; } cout << endl; return 0; }>
Java import java.util.*; public class GFG { // Function to insert a new element into the min-heap public static void insertMinHeap(List heap, int value) { // Dodajte nov element na konec kopice heap.add(value); // Pridobi indeks zadnjega elementa int index = heap.size() - 1; // Primerjaj nov element z njegovim nadrejenim in // po potrebi zamenjaj while (index> 0 && heap.get((index - 1) / 2)> heap.get(index)) { Collections.swap(heap, index, (indeks - 1) / 2); // Premakni se po drevesu navzgor do nadrejenega // elementa index = (index - 1) / 2; } } // Funkcija za brisanje vozlišča iz kopice min-heap public static void deleteMinHeap(List heap, int value) { // Poiščite indeks elementa, ki ga želite izbrisati int index = -1; za (int i = 0; i< heap.size(); i++) { if (heap.get(i) == value) { index = i; break; } } // If the element is not found, return if (index == -1) { return; } // Replace the element to be deleted with the last // element heap.set(index, heap.get(heap.size() - 1)); // Remove the last element heap.remove(heap.size() - 1); // Heapify the tree starting from the element at the // deleted index while (true) { int leftChild = 2 * index + 1; int rightChild = 2 * index + 2; int smallest = index; if (leftChild < heap.size() && heap.get(leftChild) < heap.get(smallest)) { smallest = leftChild; } if (rightChild < heap.size() && heap.get(rightChild) < heap.get(smallest)) { smallest = rightChild; } if (smallest != index) { Collections.swap(heap, index, smallest); index = smallest; } else { break; } } } // Main function to test the insertMinHeap and // deleteMinHeap functions public static void main(String[] args) { List kopica = nov ArrayList (); int[] vrednosti = { 13, 16, 31, 41, 51, 100 }; int n = values.length; za (int i = 0; i< n; i++) { insertMinHeap(heap, values[i]); } System.out.print('Initial heap: '); for (int j = 0; j < heap.size(); j++) { System.out.print(heap.get(j) + ' '); } System.out.println(); deleteMinHeap(heap, 13); System.out.print('Heap after deleting 13: '); for (int j = 0; j < heap.size(); j++) { System.out.print(heap.get(j) + ' '); } System.out.println(); } }> Python3 def insert_min_heap(heap, value): heap.append(value) index = len(heap) - 1 while index>0 in kopica[(indeks - 1) // 2]> kopica[indeks]: kopica[indeks], kopica[(indeks - 1) // 2] = kopica[(indeks - 1) // 2], kopica[ indeks] indeks = (indeks - 1) // 2 def delete_min_heap(kupica, vrednost): indeks = -1 za i v območju(len(kupica)): če kopica[i] == vrednost: indeks = i zlomi če indeks == -1: vrni kopico[indeks] = kopico[-1] kopico.pop() while True: levi_podrejeni = 2 * indeks + 1 desni_podrejeni = 2 * indeks + 2 najmanjša = indeks, če je levi_podrejeni< len(heap) and heap[left_child] < heap[smallest]: smallest = left_child if right_child < len(heap) and heap[right_child] < heap[smallest]: smallest = right_child if smallest != index: heap[index], heap[smallest] = heap[smallest], heap[index] index = smallest else: break heap = [] values = [13, 16, 31, 41, 51, 100] for value in values: insert_min_heap(heap, value) print('Initial heap:', heap) delete_min_heap(heap, 13) print('Heap after deleting 13:', heap)> C# using System; using System.Collections.Generic; class MinHeap { private List kopica = nov seznam (); public void Insert(int value) { heap.Add(value); int indeks = heap.Count - 1; medtem ko (indeks> 0 && kup [(indeks - 1) / 2]> kup [indeks]) { Zamenjaj (indeks, (indeks - 1) / 2); indeks = (indeks - 1) / 2; } } public void Delete(int value) { int index = heap.IndexOf(value); if (index == -1) { return; } kopica[indeks] = kopica[kopica.Število - 1]; heap.RemoveAt(heap.Count - 1); medtem ko (true) { int leviOtrok = 2 * indeks + 1; int rightChild = 2 * indeks + 2; int najmanjši = indeks; če (levo Otrok< heap.Count && heap[leftChild] < heap[smallest]) { smallest = leftChild; } if (rightChild < heap.Count && heap[rightChild] < heap[smallest]) { smallest = rightChild; } if (smallest != index) { Swap(index, smallest); index = smallest; } else { break; } } } private void Swap(int i, int j) { int temp = heap[i]; heap[i] = heap[j]; heap[j] = temp; } public void Print() { for (int i = 0; i < heap.Count; i++) { Console.Write(heap[i] + ' '); } Console.WriteLine(); } } class Program { static void Main(string[] args) { MinHeap heap = new MinHeap(); int[] values = { 13, 16, 31, 41, 51, 100 }; for (int i = 0; i < values.Length; i++) { heap.Insert(values[i]); } Console.Write('Initial heap: '); heap.Print(); heap.Delete(13); Console.Write('Heap after deleting 13: '); heap.Print(); } }> Javascript function insertMinHeap(heap, value) { // Add the new element to the end of the heap heap.push(value); // Get the index of the last element let index = heap.length - 1; // Compare the new element with its parent and swap if necessary for (let flr = Math.floor((index - 1) / 2); index>0 && kopica[flr]> kopica[indeks]; flr = Math.floor((index - 1) / 2)) { [kup [indeks], kup [flr]] = [ kup [flr], kup [indeks], ]; // Premakni se po drevesu navzgor do nadrejenega elementa index = Math.floor((index - 1) / 2); } } function deleteMinHeap(heap, value) { // Poiščite indeks elementa, ki ga želite izbrisati let index = -1; za (naj bo i = 0; i< heap.length; i++) { if (heap[i] == value) { index = i; break; } } // If the element is not found, return if (index == -1) { return; } // Replace the element to be deleted with the last element heap[index] = heap[heap.length - 1]; // Remove the last element heap.pop(); // Heapify the tree starting from the element at the deleted index while (true) { let left_child = 2 * index + 1; let right_child = 2 * index + 2; let smallest = index; if (left_child < heap.length && heap[left_child] < heap[smallest]) { smallest = left_child; } if (right_child < heap.length && heap[right_child] < heap[smallest]) { smallest = right_child; } if (smallest != index) { [heap[index], heap[smallest]] = [heap[smallest], heap[index]]; index = smallest; } else { break; } } } // Main function to test the insertMinHeap and deleteMinHeap functions let heap = []; let values = [13, 16, 31, 41, 51, 100]; for (let i = 0; i < values.length; i++) { insertMinHeap(heap, values[i]); } console.log('Initial heap: ' + heap.join(' ')); deleteMinHeap(heap, 13); console.log('Heap after deleting 13: ' + heap.join(' '));> Izhod
Initial heap: 13 16 31 41 51 100 Heap after deleting 13: 16 41 31 100 51>
Časovna zapletenost : O(log n), kjer je n št. elementov v kupu
Pomožni prostor: O(n)
3. Operacija Peek na podatkovni strukturi Min-Heap:
Za dostop do minimalnega elementa (tj. korena kopice) se vrne vrednost korenskega vozlišča. Časovna kompleksnost pokukanja v min heap je O(1).
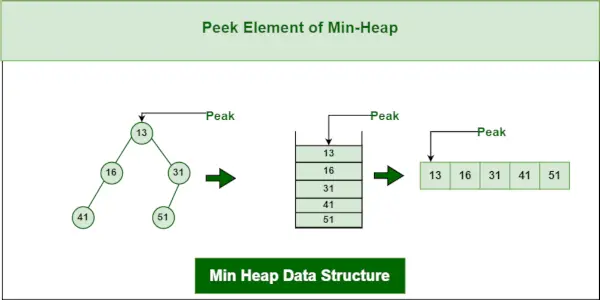
Najmanjša podatkovna struktura kopice
Implementacija operacije Peek v Min-Heap:
C++ #include #include #include using namespace std; int main() { // Create a max heap with some elements using a // priority_queue priority_queue , večji > minHeap; minHeap.push(9); minHeap.push(8); minHeap.push(7); minHeap.push(6); minHeap.push(5); minHeap.push(4); minHeap.push(3); minHeap.push(2); minHeap.push(1); // Pridobi najvišji element (tj. največji element) int peakElement = minHeap.top(); // Natisne vrh elementa cout<< 'Peak element: ' << peakElement << std::endl; return 0; }> Java import java.util.PriorityQueue; public class GFG { public static void main(String[] args) { // Create a max heap with some elements using a // PriorityQueue PriorityQueue minHeap = nova PriorityQueue(); minHeap.add(9); minHeap.add(8); minHeap.add(7); minHeap.add(6); minHeap.add(5); minHeap.add(4); minHeap.add(3); minHeap.add(2); minHeap.add(1); // Pridobite najvišji element (tj. največji element) int peakElement = minHeap.peek(); // Izpis elementa vrha System.out.println('Element vrha: ' + peakElement); } }> Python3 import heapq # Create a min heap with some elements using a list min_heap = [9, 8, 7, 6, 5, 4, 3, 2, 1] heapq.heapify(min_heap) # Get the peak element (i.e., the smallest element) peak_element = heapq.nsmallest(1, min_heap)[0] # Print the peak element print('Peak element:', peak_element)> C# using System; using System.Collections.Generic; public class GFG { public static void Main() { // Create a min heap with some elements using a // PriorityQueue var minHeap = new PriorityQueue (); minHeap.Enqueue(9); minHeap.Enqueue(8); minHeap.Enqueue(7); minHeap.Enqueue(6); minHeap.Enqueue(5); minHeap.Enqueue(4); minHeap.Enqueue(3); minHeap.Enqueue(2); minHeap.Enqueue(1); // Pridobite najvišji element (tj. najmanjši element) int peakElement = minHeap.Peek(); // Izpis elementa vrha Console.WriteLine('Element vrha: ' + peakElement); } }> Javascript const PriorityQueue = require('fast-priority-queue'); // Create a min heap with some elements using a PriorityQueue const minHeap = new PriorityQueue((a, b) =>a - b); minHeap.add(9); minHeap.add(8); minHeap.add(7); minHeap.add(6); minHeap.add(5); minHeap.add(4); minHeap.add(3); minHeap.add(2); minHeap.add(1); // Pridobite najvišji element (tj. najmanjši element) const peakElement = minHeap.peek(); // Natisni element vrha console.log(`Element vrha: ${peakElement}`);> Izhod
Peak element: 1>
Časovna zapletenost : V minimalni kopici, implementirani z uporabo matrike ali seznama, je do elementa vrha mogoče dostopati v konstantnem času, O(1), saj se vedno nahaja v korenu kopice.
V minimalnem kupu, implementiranem z binarnim drevesom, je do elementa vrha mogoče dostopati tudi v O(1) času, saj se vedno nahaja v korenu drevesa.
Pomožni prostor: O(n)
15 od 100,00
4. Operacija Heapify na podatkovni strukturi Min-Heap:
Operacijo kopičenja lahko uporabite za ustvarjanje najmanjše kopice iz nerazvrščene matrike. To naredite tako, da začnete pri zadnjem nelistnem vozlišču in večkrat izvedete operacijo mehurčka navzdol, dokler vsa vozlišča ne izpolnjujejo lastnosti kopice.
Operacija Heapify v Min Heap
Implementacija operacije Heapify v Min-Heap:
C++ #include #include using namespace std; void minHeapify(vector &arr, int i, int n) { int najmanjši = i; int l = 2*i + 1; int r = 2*i + 2; če (l< n && arr[l] < arr[smallest]) smallest = l; if (r < n && arr[r] < arr[smallest]) smallest = r; if (smallest != i) { swap(arr[i], arr[smallest]); minHeapify(arr, smallest, n); } } int main() { vector arr = {10, 5, 15, 2, 20, 30}; cout<< 'Original array: '; for (int i = 0; i < arr.size(); i++) cout << arr[i] << ' '; // Perform heapify operation on min-heap for (int i = arr.size()/2 - 1; i>= 0; i--) minHeapify(arr, i, arr.size()); cout<< '
Min-Heap after heapify operation: '; for (int i = 0; i < arr.size(); i++) cout << arr[i] << ' '; return 0; }>
Java // Java code of Heapify operation in Min-Heap import java.util.Arrays; import java.util.List; public class Main { // Function to maintain the min-heap property of the heap rooted at index 'i' public static void minHeapify(List arr, int i, int n) { // Predpostavimo, da je koren najmanjši element na začetku int smallest = i; // Izračunajte indekse levega in desnega podrejenega trenutnega vozlišča int l = 2 * i + 1; int r = 2 * i + 2; // Primerjaj levega otroka s trenutnim najmanjšim if (l< n && arr.get(l) < arr.get(smallest)) smallest = l; // Compare the right child with the current smallest if (r < n && arr.get(r) < arr.get(smallest)) smallest = r; // If the current node is not the smallest, swap it with the smallest child if (smallest != i) { int temp = arr.get(i); arr.set(i, arr.get(smallest)); arr.set(smallest, temp); // Recursively heapify the subtree rooted at the smallest child minHeapify(arr, smallest, n); } } public static void main(String[] args) { // Create a list representing the array List arr = Arrays.asList(10, 5, 15, 2, 20, 30); System.out.print('Izvirna matrika: '); // Natisni izvirno matriko za (int i = 0; i< arr.size(); i++) System.out.print(arr.get(i) + ' '); // Perform heapify operation on the min-heap // Start from the last non-leaf node and go up to the root of the tree for (int i = arr.size() / 2 - 1; i>= 0; i--) minHeapify(arr, i, arr.size()); System.out.print('
Min-Heap po operaciji heapify: '); // Natisni min-heap po operaciji heapify za (int i = 0; i< arr.size(); i++) System.out.print(arr.get(i) + ' '); } }> Python def minHeapify(arr, i, n): smallest = i left = 2 * i + 1 right = 2 * i + 2 if left < n and arr[left] < arr[smallest]: smallest = left if right < n and arr[right] < arr[smallest]: smallest = right if smallest != i: arr[i], arr[smallest] = arr[smallest], arr[i] minHeapify(arr, smallest, n) if __name__ == '__main__': arr = [10, 5, 15, 2, 20, 30] print('Original array:', arr) # Perform heapify operation on a min-heap for i in range(len(arr) // 2 - 1, -1, -1): minHeapify(arr, i, len(arr)) print('Min-Heap after heapify operation:', arr)> C# using System; using System.Collections.Generic; class GFG { // Function to perform the minHeapify operation on a min-heap. static void MinHeapify(List arr, int i, int n) { int najmanjši = i; int levo = 2 * i + 1; int desno = 2 * i + 2; // Primerjaj levega otroka s trenutno najmanjšim vozliščem. če (levo< n && arr[left] < arr[smallest]) smallest = left; // Compare the right child with the current smallest node. if (right < n && arr[right] < arr[smallest]) smallest = right; // If the current node is not the smallest // swap it with the smallest child. if (smallest != i) { int temp = arr[i]; arr[i] = arr[smallest]; arr[smallest] = temp; // Recursively call minHeapify on the affected subtree. MinHeapify(arr, smallest, n); } } static void Main(string[] args) { List arr = nov seznam { 10, 5, 15, 2, 20, 30 }; Console.Write('Izvirna matrika: '); foreach (int num in arr) Console.Write(num + ' '); // Izvedite operacijo heapify na min-heap. for (int i = arr.Count / 2 - 1; i>= 0; i--) MinHeapify(arr, i, arr.Count); Console.Write('
Min-Heap po operaciji heapify: '); foreach (int num in arr) Console.Write(num + ' '); } }> Javascript // Define a function to perform min-heapify operation on an array function minHeapify(arr, i, n) { let smallest = i; let l = 2 * i + 1; let r = 2 * i + 2; // Check if left child is smaller than the current smallest element if (l < n && arr[l] < arr[smallest]) smallest = l; // Check if right child is smaller than the current smallest element if (r < n && arr[r] < arr[smallest]) smallest = r; // If the smallest element is not the current element, swap them if (smallest !== i) { [arr[i], arr[smallest]] = [arr[smallest], arr[i]]; minHeapify(arr, smallest, n); } } // Main function function main() { const arr = [10, 5, 15, 2, 20, 30]; // Print the original array console.log('Original array: ' + arr.join(' ')); // Perform heapify operation on the min-heap for (let i = Math.floor(arr.length / 2) - 1; i>= 0; i--) minHeapify(arr, i, arr.length); // Natisni min-heap po operaciji heapify console.log('Min-heap po operaciji heapify: ' + arr.join(' ')); } // Pokliči glavno funkcijo za zagon procesa main();> Izhod
Original array: 10 5 15 2 20 30 Min-Heap after heapify operation: 2 5 15 10 20 30>
Časovna kompleksnost heapify v min-heap je O(n).
5. Operacija iskanja v strukturi podatkov Min-Heap:
Če želite poiskati element v minimalni kopici, lahko izvedete linearno iskanje po matriki, ki predstavlja kopico. Vendar pa je časovna kompleksnost linearnega iskanja O(n), kar ni učinkovito. Zato iskanje ni pogosto uporabljena operacija v kopici min.
Tukaj je primer kode, ki prikazuje, kako poiskati element v kopici min z uporabo std::najdi() :
C++ #include using namespace std; int main() { priority_queue , večji > min_heap; // primer največjega kupa min_heap.push(10); min_heap.push(9); min_heap.push(8); min_heap.push(6); min_heap.push(4); int element = 6; // element za iskanje bool found = false; // Kopirajte najmanjšo kopico v začasno čakalno vrsto in poiščite // element std::priority_queue , večji > temp = min_heap; medtem ko (!temp.empty()) { if (temp.top() == element) { najdeno = res; odmor; } temp.pop(); } če (najdeno) { std::cout<< 'Element found in the min heap.' << std::endl; } else { std::cout << 'Element not found in the min heap.' << std::endl; } return 0; }> Java import java.util.PriorityQueue; public class GFG { public static void main(String[] args) { PriorityQueue min_heap = nova PriorityQueue(); min_heap.add(3); // vstavi elemente v prednostno čakalno vrsto min_heap.offer(1); min_heap.offer(4); min_heap.offer(1); min_heap.offer(6); int element = 6; // element za iskanje boolean found = false; // Kopiraj min kopico v začasno čakalno vrsto in poišči // element PriorityQueue temp = nova PriorityQueue(min_heap); medtem ko (!temp.isEmpty()) { if (temp.poll() == element) { najdeno = res; odmor; } } if (found) { System.out.println( 'Element najden v min heap.'); } else { System.out.println( 'Element ni bil najden v min kopici.'); } } }> Python3 import heapq min_heap = [1, 2, 3, 5, 6, 7, 8, 10] # example min heap heapq.heapify(min_heap) element = 6 # element to search for found = False # Copy the min heap to a temporary list and search for the element temp = list(min_heap) while temp: if heapq.heappop(temp) == element: found = True break if found: print('Element found in the min heap.') else: print('Element not found in the min heap.')> C# using System; using System.Collections.Generic; public class GFG { public static void Main() { var minHeap = new PriorityQueue (); // primer min kopice minHeap.Enqueue(4); minHeap.Enqueue(6); minHeap.Enqueue(8); minHeap.Enqueue(9); minHeap.Enqueue(10); int element = 6; // element za iskanje bool found = false; // Kopiraj min kopico v začasno čakalno vrsto in poišči // element var temp = new PriorityQueue (minHeap); medtem ko (temp.Count> 0) { if (temp.Peek() == element) { najdeno = res; odmor; } temp.Dequeue(); } if (najdeno) { Console.WriteLine( 'Element najden v min kopici.'); } else { Console.WriteLine( 'Element ni bil najden v kopici min.'); } } }> Javascript // Example min heap let minHeap = new PriorityQueue(); minHeap.enqueue(4); minHeap.enqueue(6); minHeap.enqueue(8); minHeap.enqueue(9); minHeap.enqueue(10); let element = 6; // Element to search for let found = false; // Copy the min heap to a temporary queue and search for the element let temp = new PriorityQueue(minHeap); while (temp.size()>0) { if (temp.peek() == element) { najdeno = res; odmor; } temp.dequeue(); } if (najdeno) { console.log('Element najden v min kopici.'); } else { console.log('Element ni bil najden v kopici min.'); }> Izhod
Element found in the min heap.>
Analiza kompleksnosti :
The časovna kompleksnost tega programa je O(n log n) , kje n je število elementov v prednostni čakalni vrsti.
Operacija vstavljanja je časovno zahtevna O(log n) v najslabšem primeru, ker je treba ohraniti lastnost kopice. Operacija iskanja vključuje kopiranje prednostne čakalne vrste v začasno čakalno vrsto in nato prečkanje začasne čakalne vrste, kar traja O(n log n) čas v najslabšem primeru, ker je treba vsak element kopirati in odstraniti iz čakalne vrste, prednostno čakalno vrsto pa je treba znova zgraditi za vsako operacijo.
The kompleksnost prostora programa je O(n) ker shranjuje n elementov v prednostni čakalni vrsti in ustvari začasno čakalno vrsto z n elementi.
Aplikacije strukture podatkov Min-Heap:
- Razvrstitev kopice: Najmanjša kopica se uporablja kot ključna komponenta v algoritmu za razvrščanje kopice, ki je učinkovit algoritem za razvrščanje s časovno kompleksnostjo O(nlogn).
- Prednostna čakalna vrsta: Prednostno čakalno vrsto je mogoče implementirati s podatkovno strukturo najmanjše kopice, kjer je element z najmanjšo vrednostjo vedno v korenu.
- Dijkstrajev algoritem: V Dijkstrovem algoritmu se minimalna kopica uporablja za shranjevanje oglišč grafa z najmanjšo razdaljo od začetne oglišča. Točka z najmanjšo razdaljo je vedno v korenu kupa.
- Huffmanovo kodiranje: Pri Huffmanovem kodiranju se minimalni kup uporablja za implementacijo prednostne čakalne vrste za izgradnjo optimalne kode predpone za dani nabor znakov.
- Spoji K razvrščenih nizov: Če imamo K razvrščenih nizov, jih lahko učinkovito združimo v en sam razvrščen niz z uporabo podatkovne strukture najmanj kopice.
Prednosti strukture podatkov Min-heap:
- Učinkovito vstavljanje in brisanje : Najmanjša kopica omogoča hitro vstavljanje in brisanje elementov s časovno kompleksnostjo O(log n), kjer je n število elementov v kopici.
- Učinkovito iskanje najmanjšega elementa: Najmanjši element v kopici min je vedno v korenu kopice, ki ga je mogoče pridobiti v O(1) času.
- Prostorsko učinkovito: Najmanjša kopica je kompaktna podatkovna struktura, ki jo je mogoče implementirati z uporabo matrike ali binarnega drevesa, zaradi česar je prostorsko učinkovita.
- Razvrščanje: Najmanjšo kopico je mogoče uporabiti za implementacijo učinkovitega algoritma za razvrščanje, kot je sortiranje kopice s časovno kompleksnostjo O(n log n).
- Prednostna čakalna vrsta: Najmanjšo kopico je mogoče uporabiti za implementacijo prednostne čakalne vrste, kjer je mogoče element z najmanjšo prioriteto učinkovito pridobiti v O(1) času.
- Vsestranskost: Min heap ima več aplikacij v računalništvu, vključno z algoritmi grafov, stiskanjem podatkov in sistemi baz podatkov.
Na splošno je min heap uporabna in vsestranska podatkovna struktura, ki ponuja učinkovite operacije, prostorsko učinkovitost in ima več aplikacij v računalništvu.