Binarno iskalno drevo je podatkovna struktura, ki se uporablja v računalništvu za organiziranje in shranjevanje podatkov na razvrščen način. Binarno iskalno drevo sledi vsem lastnostim binarnega drevesa in njegovih levo otrok vsebuje vrednosti, manjše od nadrejenega vozlišča in prav otrok vsebuje vrednosti, večje od nadrejenega vozlišča. Ta hierarhična struktura omogoča učinkovito Iskanje , Vstavljanje , in Izbris operacije na podatkih, shranjenih v drevesu.
kako razvrstiti arraylist v Javi
Binarno iskalno drevo
Kazalo
- Kaj je binarno iskalno drevo?
- Lastnosti binarnega iskalnega drevesa
- Ravnanje s podvojenimi vrednostmi v binarnem iskalnem drevesu
- Operacije, izvedene na BST
- 1. Iskanje vozlišča v BST
- 2. Vstavite vozlišče v BST
- 3. Izbrišite vozlišče BST
- 4. Prehod (prehod po nevrstnem redu BST)
- Aplikacije BST
- Prednosti
- Slabosti
- Pogosta vprašanja (pogosta vprašanja) o drevesu binarnega iskanja:
Kaj je binarno iskalno drevo?
Binarno iskalno drevo (BST) je posebna vrsta binarno drevo v kateri ima levi podrejeni element vozlišča vrednost, nižjo od vrednosti vozlišča, desni podrejeni element pa ima vrednost, ki je večja od vrednosti vozlišča. Ta lastnost se imenuje lastnost BST in omogoča učinkovito iskanje, vstavljanje in brisanje elementov v drevesu.
Lastnosti binarnega iskalnega drevesa:
- Levo poddrevo vozlišča vsebuje samo vozlišča s ključi, ki so manjši od ključa vozlišča.
- Desno poddrevo vozlišča vsebuje samo vozlišča s ključi, večjimi od ključa vozlišča.
- To pomeni, da je vse levo od korena manjše od vrednosti korena in vse desno od korena večje od vrednosti korena. Zaradi tega delovanja je binarno iskanje zelo enostavno.
- Levo in desno poddrevo morata biti tudi binarno iskalno drevo.
- Ne sme biti podvojenih vozlišč (BST ima lahko podvojene vrednosti z različnimi pristopi ravnanja)
Ravnanje s podvojenimi vrednostmi v binarnem iskalnem drevesu:
- Vseskozi moramo slediti doslednemu postopku, tj. shraniti podvojeno vrednost na levi ali shraniti podvojeno vrednost na desni strani korena, vendar bodimo dosledni s svojim pristopom.
Osnovne operacije na binarnem iskalnem drevesu:
1. Iskanje vozlišča v BST:
Iskanje v BST pomeni iskanje določenega vozlišča v podatkovni strukturi. V binarnem iskalnem drevesu je iskanje vozlišča preprosto zaradi njegovega posebnega vrstnega reda. Koraki iskanja vozlišča v drevesu binarnega iskanja so navedeni na naslednji način –
- Najprej primerjajte element, ki ga želite iskati, s korenskim elementom drevesa.
- Če se koren ujema s ciljnim elementom, vrni lokacijo vozlišča.
- Če se ne ujema, preverite, ali je element manjši od korenskega elementa, če je manjši od korenskega elementa, se premaknite na levo poddrevo.
- Če je večji od korenskega elementa, se pomaknite na desno poddrevo.
- Ponavljajte zgornji postopek rekurzivno, dokler ne najdete ujemanja.
- Če elementa ni mogoče najti ali ni prisoten v drevesu, vrnite NULL.
Zdaj pa poglejmo iskanje v binarnem drevesu na primeru:
Spodaj je podan BST in poiskati moramo element 6.
Koda:
Spodaj je implementacija iskanja v BST:
C++ // C++ function to search a given key in a given BST #include using namespace std; struct node { int key; struct node *left, *right; }; // A utility function to create a new BST node struct node* newNode(int item) { struct node* temp = new struct node; temp->ključ = predmet; temp->levo = temp->desno = NULL; povratna temperatura; } // Pomožna funkcija za vstavljanje // novega vozlišča z danim ključem v BST struct node* insert(struct node* node, int key) { // Če je drevo prazno, vrni novo vozlišče if (node == NULL ) vrni novoVozlišče(ključ); // V nasprotnem primeru se ponovi po drevesu, če (ključ< node->ključ) vozlišče->levo = vstavi(vozlišče->levo, ključ); else if (ključ> vozlišče->ključ) vozlišče->desno = vstavi(vozlišče->desno, ključ); // Vrni (nespremenjen) kazalec vozlišča return node; } // Pomožna funkcija za iskanje ključa v BST struct node* search(struct node* root, int key) root->key == key) return root; // Ključ je večji od korenskega ključa, če (root->key< key) return search(root->desno, ključ); // Ključ je manjši od korenskega ključa vrni iskanje (root->left, key);> C // C function to search a given key in a given BST #include #include struct node { int key; struct node *left, *right; }; // A utility function to create a new BST node struct node* newNode(int item) { struct node* temp = (struct node*)malloc(sizeof(struct node)); temp->ključ = predmet; temp->levo = temp->desno = NULL; povratna temperatura; } // Pomožna funkcija za vstavljanje // novega vozlišča z danim ključem v BST struct node* insert(struct node* node, int key) { // Če je drevo prazno, vrni novo vozlišče if (node == NULL ) vrni novoVozlišče(ključ); // V nasprotnem primeru se ponovi po drevesu, če (ključ< node->ključ) vozlišče->levo = vstavi(vozlišče->levo, ključ); else if (ključ> vozlišče->ključ) vozlišče->desno = vstavi(vozlišče->desno, ključ); // Vrni (nespremenjen) kazalec vozlišča return node; } // Pomožna funkcija za iskanje ključa v BST struct node* search(struct node* root, int key)> Java // Java program to search a given key in a given BST class Node { int key; Node left, right; public Node(int item) { key = item; left = right = null; } } class BinarySearchTree { Node root; // Constructor BinarySearchTree() { root = null; } // A utility function to insert // a new node with given key in BST Node insert(Node node, int key) { // If the tree is empty, return a new node if (node == null) { node = new Node(key); return node; } // Otherwise, recur down the tree if (key < node.key) node.left = insert(node.left, key); else if (key>vozlišče.ključ) vozlišče.desno = vstavi(vozlišče.desno, ključ); // Vrni (nespremenjen) kazalec vozlišča return node; } // Pomožna funkcija za iskanje ključa pri iskanju vozlišča BST (koren vozlišča, int ključ) // Osnovni primeri: koren je nič ali je ključ prisoten v korenu, če (root == null> Python # Python3 function to search a given key in a given BST class Node: # Constructor to create a new node def __init__(self, key): self.key = key self.left = None self.right = None # A utility function to insert # a new node with the given key in BST def insert(node, key): # If the tree is empty, return a new node if node is None: return Node(key) # Otherwise, recur down the tree if key < node.key: node.left = insert(node.left, key) elif key>node.key: node.right = insert(node.right, key) # Vrni (nespremenjen) kazalec vozlišča return node # Pomožna funkcija za iskanje ključa v BST def search(root, key): # Osnovni primeri: root je null ali ključ je prisoten v korenu, če je root None ali root.key == ključ: vrni koren # Ključ je večji od korenskega ključa, če je root.key< key: return search(root.right, key) # Key is smaller than root's key return search(root.left, key)>
JavaScript // Javascript function to search a given key in a given BST class Node { constructor(key) { this.key = key; this.left = null; this.right = null; } } // A utility function to insert // a new node with given key in BST function insert(node, key) { // If the tree is empty, return a new node if (node === null) { return new Node(key); } // Otherwise, recur down the tree if (key < node.key) { node.left = insert(node.left, key); } else if (key>vozlišče.ključ) { vozlišče.desno = vstavi(vozlišče.desno, ključ); } // Vrni (nespremenjen) kazalec vozlišča return node; } // Pomožna funkcija za iskanje ključa v funkciji BST search(root, key) { // Osnovni primeri: root je nič ali je ključ prisoten v root if (root === null || root.key === key ) { vrni koren; } // Ključ je večji od korenskega ključa, če (root.key< key) { return search(root.right, key); } // Key is smaller than root's key return search(root.left, key); }>
2. Vstavite vozlišče v BST :
Nov ključ se vedno vstavi na list. Začnite iskati ključ od korena do listnega vozlišča. Ko je listno vozlišče najdeno, se novo vozlišče doda kot podrejeno listnemu vozlišču.
Koda:
Spodaj je implementacija vstavljanja enega samega vozlišča v binarno iskalno drevo:
struktura podatkovC++
// Given Node Structure struct node { int key; struct node *left, *right; }; // Function to create a new BST node struct node* newNode(int item) { struct node* temp = (struct node*)malloc( sizeof(struct node)); temp->ključ = predmet; temp->levo = temp->desno = NULL; povratna temperatura; } // Funkcija za vstavljanje novega vozlišča z // danim ključem v BST struct node* insert(struct node* node, int key) { // Če je drevo prazno, vrni novo vozlišče if (node == NULL) return novoVozlišče(ključ); // V nasprotnem primeru se ponovi po drevesu, če (ključ< node->ključ) { vozlišče->levo = vstavi(vozlišče->levo, ključ); } else if (ključ> vozlišče->ključ) { vozlišče->desno = vstavi(vozlišče->desno, ključ); } // Vrne kazalec vozlišča return node; }> C // Given Node Structure struct node { int key; struct node *left, *right; }; // Function to create a new BST node struct node* newNode(int item) { struct node* temp = (struct node*)malloc( sizeof(struct node)); temp->ključ = predmet; temp->levo = temp->desno = NULL; povratna temperatura; } // Funkcija za vstavljanje novega vozlišča z // danim ključem v BST struct node* insert(struct node* node, int key) { // Če je drevo prazno, vrni novo vozlišče if (node == NULL) return novoVozlišče(ključ); // V nasprotnem primeru se ponovi po drevesu, če (ključ< node->ključ) { vozlišče->levo = vstavi(vozlišče->levo, ključ); } else if (ključ> vozlišče->ključ) { vozlišče->desno = vstavi(vozlišče->desno, ključ); } // Vrne kazalec vozlišča return node; }> Java class GFG { // Given Node Structure static class node { int key; node left, right; }; // Function to create a new BST node static node newNode(int item) { node temp = new node(); temp.key = item; temp.left = temp.right = null; return temp; } // Function to insert a new node with // given key in BST static node insert(node node, int key) { // If the tree is empty, return a new node if (node == null) return newNode(key); // Otherwise, recur down the tree if (key < node.key) { node.left = insert(node.left, key); } else if (key>vozlišče.ključ) { vozlišče.desno = vstavi(vozlišče.desno, ključ); } // Vrne vozlišče return node; } }> Python3 # Given Node Structure class Node: def __init__(self, key): self.key = key self.left = None self.right = None # Function to insert a new node with # given key in BST def insert(node, key): # If the tree is empty, return a new node if node is None: return Node(key) # Otherwise, recur down the tree if key < node.key: node.left = insert(node.left, key) elif key>node.key: node.right = insert(node.right, key) # Vrni kazalec vozlišča vrni vozlišče>
Javascript // Given Node Structure class Node { constructor(key){ this.key = key; this.left = null; this.right = null; } } // Function to insert a new node with // given key in BST function insert(node, key) { // If the tree is empty, return a new node if (node == null) return new Node(key); // Otherwise, recur down the tree if (key < node.key) { node.left = insert(node.left, key); } else if (key>vozlišče.ključ) { vozlišče.desno = vstavi(vozlišče.desno, ključ); } // Vrne kazalec vozlišča return node; }> Časovna zapletenost: O(N), kjer je N število vozlišč BST
Pomožni prostor: O(1)
3. Izbrišite vozlišče BST :
Uporablja se za brisanje vozlišča z določenim ključem iz BST in vrnitev novega BST.
Različni scenariji za brisanje vozlišča:
Vozlišče, ki ga želite izbrisati, je listno vozlišče :
Preprosto je, lahko ga preprosto izničite.
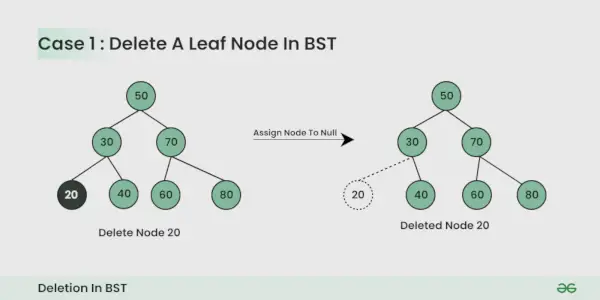
Vozlišče, ki ga želite izbrisati, ima enega podrejenega :
Vozlišče lahko preprosto zamenjate s podrejenim vozliščem.
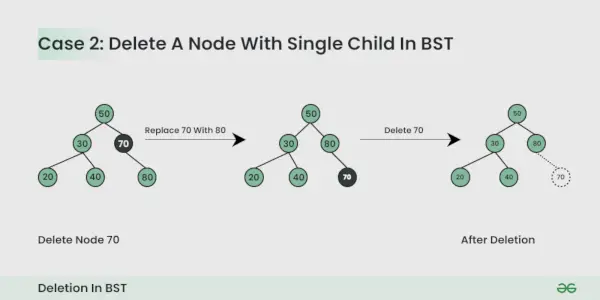
Vozlišče, ki ga želite izbrisati, ima dva otroka :
Tukaj moramo brisanje vozlišča je tako, da nastalo drevo sledi lastnostim BST. Trik je najti naslednika vozlišča po vrstnem redu. Kopirajte vsebino naslednika vrstnega reda v vozlišče in izbrišite naslednika vrstnega reda.
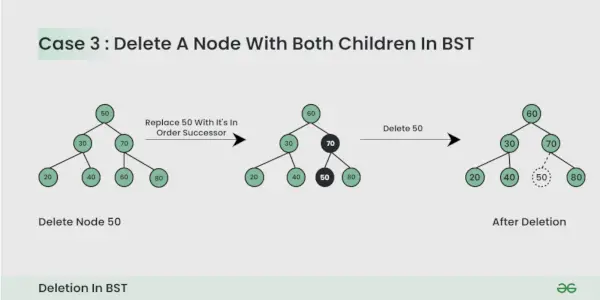
Med brisanjem vozlišča BST bodite pozorni na naslednje:
- Treba je ugotoviti, kakšna bo zamenjava vozlišča, ki ga želite izbrisati.
- Želite minimalne motnje v obstoječi drevesni strukturi
- Lahko vzame nadomestno vozlišče iz izbrisanih vozlišč levo ali desno poddrevo.
- Če vzamemo if iz levega poddrevesa, moramo vzeti največjo vrednost v levem poddrevesu.
- Če vzamemo if iz desnega poddrevesa, moramo vzeti najmanjšo vrednost v desnem poddrevesu.
Koda:
Spodaj je izvedba izbrisa v BST:
C++ // C++ program to delete // a node of BST // Given Node node struct node { int key; struct node *left, *right; }; // Function to create a new BST node struct node* newNode(int item) { struct node* temp = (struct node*)malloc( sizeof(struct node)); temp->ključ = predmet; temp->levo = temp->desno = NULL; povratna temperatura; } // Funkcija za vstavljanje novega vozlišča z // danim ključem v BST struct node* insert(struct node* node, int key) { // Če je drevo prazno, vrni novo vozlišče if (node == NULL) return novoVozlišče(ključ); // V nasprotnem primeru se ponovi po drevesu, če (ključ< node->ključ) { vozlišče->levo = vstavi(vozlišče->levo, ključ); } else if (ključ> vozlišče->ključ) { vozlišče->desno = vstavi(vozlišče->desno, ključ); } // Vrne kazalec vozlišča return node; } // Funkcija, ki vrne vozlišče z najmanjšo // ključno vrednostjo, najdeno v tem drevesu struct node* minValueNode(struct node* node) { struct node* current = node; // Zanka navzdol, da poiščemo skrajni levi list, medtem ko (trenutno && trenutno->levo != NULL) trenutno = trenutno->levo; povratni tok; } // Funkcija, ki izbriše ključ in // vrne novo korensko vozlišče struct node* deleteNode(struct node* root, int key) { // osnovni primer if (root == NULL) return root; // Če je ključ, ki ga želite izbrisati, // manjši od korenskega ključa, // potem leži v levem poddrevesu, če (ključ< root->ključ) { root->left = deleteNode(root->left, key); } // Če je ključ, ki ga želite izbrisati, // večji od korenskega ključa, // potem leži v desnem poddrevesu else if (ključ> koren->ključ) { koren->desno = deleteNode(root-> desno, ključ); } // Če je ključ enak kot korenski ključ, // potem je to vozlišče // za brisanje else { // Vozlišče s samo enim podrejenim // ali brez podrejenega, če (root->left == NULL) {struct node* temp = root->right; brezplačno (koren); povratna temperatura; } else if (root->right == NULL) { struct node* temp = root->left; brezplačno (koren); povratna temperatura; } // Vozlišče z dvema otrokoma: // Pridobite naslednika po vrstnem redu (najmanjši // v desnem poddrevesu) struct vozlišče* temp = minValueNode(root->right); // Kopiraj vsebino naslednika po vrstnem redu v to vozlišče root->key = temp->key; // Brisanje naslednika po vrstnem redu root->right = deleteNode(root->right, temp->key); } vrni koren; }> C // C program to delete // a node of BST // Given Node node struct node { int key; struct node *left, *right; }; // Function to create a new BST node struct node* newNode(int item) { struct node* temp = (struct node*)malloc( sizeof(struct node)); temp->ključ = predmet; temp->levo = temp->desno = NULL; povratna temperatura; } // Funkcija za vstavljanje novega vozlišča z // danim ključem v BST struct node* insert(struct node* node, int key) { // Če je drevo prazno, vrni novo vozlišče if (node == NULL) return novoVozlišče(ključ); // V nasprotnem primeru se ponovi po drevesu, če (ključ< node->ključ) { vozlišče->levo = vstavi(vozlišče->levo, ključ); } else if (ključ> vozlišče->ključ) { vozlišče->desno = vstavi(vozlišče->desno, ključ); } // Vrne kazalec vozlišča return node; } // Funkcija, ki vrne vozlišče z najmanjšo // ključno vrednostjo, najdeno v tem drevesu struct node* minValueNode(struct node* node) { struct node* current = node; // Zanka navzdol, da poiščemo skrajni levi list, medtem ko (trenutno && trenutno->levo != NULL) trenutno = trenutno->levo; povratni tok; } // Funkcija, ki izbriše ključ in // vrne novo korensko vozlišče struct node* deleteNode(struct node* root, int key) { // osnovni primer if (root == NULL) return root; // Če je ključ, ki ga želite izbrisati, // manjši od korenskega ključa, // potem leži v levem poddrevesu, če (ključ< root->ključ) { root->left = deleteNode(root->left, key); } // Če je ključ, ki ga želite izbrisati, // večji od korenskega ključa, // potem leži v desnem poddrevesu else if (ključ> koren->ključ) { koren->desno = deleteNode(root-> desno, ključ); } // Če je ključ enak kot korenski ključ, // potem je to vozlišče // za brisanje else { // Vozlišče samo z enim podrejenim // ali brez podrejenega, če (root->left == NULL) {struct node* temp = root->right; brezplačno (koren); povratna temperatura; } else if (root->right == NULL) { struct node* temp = root->left; brezplačno (koren); povratna temperatura; } // Vozlišče z dvema otrokoma: // Pridobite naslednika po vrstnem redu (najmanjši // v desnem poddrevesu) struct vozlišče* temp = minValueNode(root->right); // Kopiraj vsebino naslednika po vrstnem redu v to vozlišče root->key = temp->key; // Brisanje naslednika po vrstnem redu root->right = deleteNode(root->right, temp->key); } vrni koren; }> Java // Java program for Delete a Node of BST class GFG { // Given Node node static class node { int key; node left, right; }; // Function to create a new BST node static node newNode(int item) { node temp = new node(); temp.key = item; temp.left = temp.right = null; return temp; } // Function to insert a new node with // given key in BST static node insert(node node, int key) { // If the tree is empty, return a new node if (node == null) return newNode(key); // Otherwise, recur down the tree if (key < node.key) { node.left = insert(node.left, key); } else if (key>vozlišče.ključ) { vozlišče.desno = vstavi(vozlišče.desno, ključ); } // Vrne vozlišče return node; } // Funkcija, ki vrne vozlišče z najmanjšo // ključno vrednostjo, najdeno v tem drevesnem statičnem vozlišču minValueNode(vozlišče vozlišča) { trenutno vozlišče = vozlišče; // Zanka navzdol, da poiščemo skrajni levi list while (current != null && current.left != null) current = current.left; povratni tok; } // Funkcija, ki izbriše ključ in // vrne novo korensko statično vozlišče deleteNode(node root, int key) { // osnovni primer if (root == null) return root; // Če je ključ, ki ga želite izbrisati, // manjši od korenskega ključa, // potem leži v levem poddrevesu, če (ključ< root.key) { root.left = deleteNode(root.left, key); } // If the key to be deleted is // greater than the root's key, // then it lies in right subtree else if (key>root.key) { root.right = deleteNode(root.right, key); } // Če je ključ enak kot korenski ključ, // potem je to vozlišče // za brisanje else { // Vozlišče s samo enim podrejenim // ali brez podrejenega if (root.left == null) { vozlišče temp = root.right; povratna temperatura; } else if (root.right == null) { node temp = root.left; povratna temperatura; } // Vozlišče z dvema otrokoma: // Pridobite naslednika po vrstnem redu (najmanjši // v desnem poddrevesu) vozlišče temp = minValueNode(root.right); // Kopiraj vsebino naslednika po vrstnem redu v to vozlišče root.key = temp.key; // Izbriši naslednika po vrstnem redu root.right = deleteNode(root.right, temp.key); } vrni koren; }> Python # Python program to delete a node of BST # Given Node node class Node: def __init__(self, key): self.key = key self.left = None self.right = None # Function to insert a new node with # given key in BST def insert(root, key): # If the tree is empty, return a new node if root is None: return Node(key) # Otherwise, recur down the tree if key < root.key: root.left = insert(root.left, key) elif key>root.key: root.right = insert(root.right, key) # Vrni kazalec vozlišča return root # Funkcija za prečkanje BST def inorder(root): if root: inorder(root.left) print(root. key, end=' ') inorder(root.right) # Funkcija, ki vrne vozlišče z minimalno # ključno vrednostjo, najdeno v tem drevesu def minValueNode(node): current = vozlišče # Zanka navzdol, da poiščete skrajni levi list, medtem ko sta trenutno in current.left ni None: current = current.left return current # Funkcija, ki izbriše ključ in # vrne novo korensko def deleteNode(root, key): # osnovni primer, če je root None: return root # Če je ključ deleted je # manjši od korenskega ključa, # potem leži v levem poddrevesu, če je ključ< root.key: root.left = deleteNode(root.left, key) # If the key to be deleted is # greater than the root's key, # then it lies in right subtree elif key>root.key: root.right = deleteNode(root.right, key) # Če je ključ enak kot root's ključ, # potem je to vozlišče #, ki ga je treba izbrisati else: # Vozlišče samo z enim podrejenim # ali brez podrejenega if root.left is None: temp = root.right root = None return temp elif root.right is None: temp = root.left root = None return temp # Vozlišče z dvema otrokoma: # Pridobite naslednika po vrstnem redu (najmanjši # v desno poddrevo) temp = minValueNode(root.right) # Kopiraj # vsebino naslednika po vrstnem redu v to vozlišče root.key = temp.key # Izbriši naslednika po vrstnem redu root.right = deleteNode(root.right, temp.key) vrni koren>>
4. Prehod (prehod po nevrstnem redu BST) :
V primeru binarnih iskalnih dreves (BST) prečkanje po vrstnem redu daje vozlišča v nepadajočem vrstnem redu. Najprej obiščemo levega otroka, nato koren in nato desnega otroka.
Spodaj je izvedba, kako narediti prečkanje binarnega iskalnega drevesa po vrstnem redu:
C++ // C++ program to implement // inorder traversal of BST #include using namespace std; // Given Node node struct node { int key; struct node *left, *right; }; // Function to create a new BST node struct node* newNode(int item) { struct node* temp = (struct node*)malloc( sizeof(struct node)); temp->ključ = predmet; temp->levo = temp->desno = NULL; povratna temperatura; } // Funkcija za vstavljanje novega vozlišča z // danim ključem v BST struct node* insert(struct node* node, int key) { // Če je drevo prazno, vrni novo vozlišče if (node == NULL) return novoVozlišče(ključ); // V nasprotnem primeru se ponovi po drevesu, če (ključ< node->ključ) { vozlišče->levo = vstavi(vozlišče->levo, ključ); } else if (ključ> vozlišče->ključ) { vozlišče->desno = vstavi(vozlišče->desno, ključ); } // Vrne kazalec vozlišča return node; } // Funkcija za prečkanje po vrstnem redu BST void inorder(struct node* root) { if (root != NULL) { inorder(root->left); cout<< ' ' << root->ključ; inorder(root->desno); } } // Koda gonilnika int main() { /* Ustvarimo naslednji BST 50 / 30 70 / / 20 40 60 80 */ struct node* root = NULL; // Ustvarjanje korena BST = insert(root, 50); vstavi (koren, 30); vstavi (koren, 20); vstavi (koren, 40); vstavi (koren, 70); vstavi (koren, 60); vstavi (koren, 80); // Klic funkcije inorder(root); vrni 0; } // To kodo je prispeval shivanisinghss2110> C // C program to implement // inorder traversal of BST #include #include // Given Node node struct node { int key; struct node *left, *right; }; // Function to create a new BST node struct node* newNode(int item) { struct node* temp = (struct node*)malloc( sizeof(struct node)); temp->ključ = predmet; temp->levo = temp->desno = NULL; povratna temperatura; } // Funkcija za vstavljanje novega vozlišča z // danim ključem v BST struct node* insert(struct node* node, int key) { // Če je drevo prazno, vrni novo vozlišče if (node == NULL) return novoVozlišče(ključ); // V nasprotnem primeru se ponovi po drevesu, če (ključ< node->ključ) { vozlišče->levo = vstavi(vozlišče->levo, ključ); } else if (ključ> vozlišče->ključ) { vozlišče->desno = vstavi(vozlišče->desno, ključ); } // Vrne kazalec vozlišča return node; } // Funkcija za prečkanje po vrstnem redu BST void inorder(struct node* root) { if (root != NULL) { inorder(root->left); printf('%d ', root->key); inorder(root->desno); } } // Koda gonilnika int main() { /* Ustvarimo naslednji BST 50 / 30 70 / / 20 40 60 80 */ struct node* root = NULL; // Ustvarjanje korena BST = insert(root, 50); vstavi (koren, 30); vstavi (koren, 20); vstavi (koren, 40); vstavi (koren, 70); vstavi (koren, 60); vstavi (koren, 80); // Klic funkcije inorder(root); vrni 0; }> Java import java.io.*; // Java program for Inorder Traversal class GFG { // Given Node node static class node { int key; node left, right; }; // Function to create a new BST node static node newNode(int item) { node temp = new node(); temp.key = item; temp.left = temp.right = null; return temp; } // Function to insert a new node with // given key in BST static node insert(node node, int key) { // If the tree is empty, return a new node if (node == null) return newNode(key); // Otherwise, recur down the tree if (key < node.key) { node.left = insert(node.left, key); } else if (key>vozlišče.ključ) { vozlišče.desno = vstavi(vozlišče.desno, ključ); } // Vrne vozlišče return node; } // Funkcija za prečkanje po vrstnem redu BST static void inorder(node root) { if (root != null) { inorder(root.left); System.out.print(' ' + root.key); inorder(root.right); } } // Koda gonilnika public static void main(String[] args) { /* Ustvarimo naslednji BST 50 / 30 70 / / 20 40 60 80 */ koren vozlišča = nič; // vstavljanje vrednosti 50 root = insert(root, 50); // vstavljanje vrednosti 30 insert(root, 30); // vstavljanje vrednosti 20 insert(root, 20); // vstavljanje vrednosti 40 insert(root, 40); // vstavljanje vrednosti 70 insert(root, 70); // vstavljanje vrednosti 60 insert(root, 60); // vstavljanje vrednosti 80 insert(root, 80); // natisni BST inorder(root); } } // To kodo je prispeval abhijitjadhav1998> Python3 # Python program to implement # inorder traversal of BST # Given Node node class Node: def __init__(self, key): self.key = key self.left = None self.right = None # Function to create a new BST node def newNode(item): temp = Node(item) temp.key = item temp.left = temp.right = None return temp # Function to insert a new node with # given key in BST def insert(node, key): # If the tree is empty, return a new node if node is None: return newNode(key) # Otherwise, recur down the tree if key < node.key: node.left = insert(node.left, key) elif key>node.key: node.right = insert(node.right, key) # Vrni kazalec vozlišča return node # Funkcija za prečkanje po vrstnem redu BST def inorder(root): če je koren: inorder(root.left) print(root. key, end=' ') inorder(root.right) # Koda gonilnika if __name__ == '__main__': # Ustvarimo naslednji BST # 50 # / # 30 70 # / / # 20 40 60 80 root = Brez # Ustvarjanje korena BST = insert(root, 50) insert(root, 30) insert(root, 20) insert(root, 40) insert(root, 70) insert(root, 60) insert(root , 80) # Klic funkcije inorder(root) #To kodo je prispeval japmeet01>
Izhod
20 30 40 50 60 70 80>
Časovna zapletenost: O(N), kjer je N število vozlišč BST
Pomožni prostor: O(1)
Aplikacije BST:
- Algoritmi grafov: BST-je je mogoče uporabiti za implementacijo algoritmov grafov, na primer v algoritmih minimalnega vpetega drevesa.
- Prednostne čakalne vrste: BST-je je mogoče uporabiti za implementacijo prednostnih čakalnih vrst, kjer je element z najvišjo prioriteto v korenu drevesa, elementi z nižjo prioriteto pa so shranjeni v poddrevesih.
- Samouravnotežno binarno iskalno drevo: BST-je je mogoče uporabiti kot samouravnotežne podatkovne strukture, kot sta drevo AVL in rdeče-črno drevo.
- Shranjevanje in iskanje podatkov: BST-je je mogoče uporabiti za hitro shranjevanje in pridobivanje podatkov, na primer v bazah podatkov, kjer je iskanje določenega zapisa mogoče izvesti v logaritemskem času.
Prednosti:
- Hitro iskanje: Iskanje določene vrednosti v BST ima povprečno časovno kompleksnost O(log n), kjer je n število vozlišč v drevesu. To je veliko hitreje kot iskanje elementa v matriki ali povezanem seznamu, ki ima v najslabšem primeru časovno kompleksnost O(n).
- Prehod po vrstnem redu: BST je mogoče prečkati po vrstnem redu, ki obišče levo poddrevo, koren in desno poddrevo. To lahko uporabite za razvrščanje nabora podatkov.
- Prostorsko učinkovito: BST so prostorsko učinkoviti, saj ne shranjujejo nobenih odvečnih informacij, za razliko od nizov in povezanih seznamov.
Slabosti:
- Poševna drevesa: Če drevo postane poševno, bo časovna kompleksnost operacij iskanja, vstavljanja in brisanja O(n) namesto O(log n), zaradi česar je lahko drevo neučinkovito.
- Potreben dodatni čas: Samouravnotežena drevesa potrebujejo dodaten čas za vzdrževanje ravnotežja med operacijami vstavljanja in brisanja.
- Učinkovitost: BST-ji niso učinkoviti za nize podatkov s številnimi dvojniki, saj bodo zapravljali prostor.
pogosta vprašanja(Pogosto zastavljena vprašanja)na binarnem iskalnem drevesu:
1. Kaj je binarno iskalno drevo?
Binarno iskalno drevo (BST) je binarno drevo, kjer je vsako vozlišče v levem poddrevesu manjše od korena, vsako vozlišče v desnem poddrevesu pa ima večjo vrednost od korena . Lastnosti binarnega iskalnega drevesa so rekurzivne: če katero koli vozlišče obravnavamo kot koren, bodo te lastnosti ostale resnične.
2. Kaj je operacija binarnega iskalnega drevesa?
V drevesu binarnega iskanja so tri glavne operacije: 1. Vstavljanje, 2. Brisanje, 3. Iskanje. Zaradi svojih lastnosti je učinkovito iskanje po katerem koli elementu v binarnem iskalnem drevesu.
3. Kaj je binarno iskalno drevo in drevo AVL?
Binarno iskalno drevo : Binarno iskalno drevo (BST) je binarno drevo, kjer je vsako vozlišče v levem poddrevesu manjše od korena, vsako vozlišče v desnem poddrevesu pa ima večjo vrednost od korena.
Drevo AVL : Binarna iskalna drevesa (BST), ki se samodejno uravnotežijo in vrtijo, so znana kot drevesa AVL.
vprašanja za razgovor v jeziku java
4. Za kaj se uporablja binarno iskalno drevo?
Binarna iskalna drevesa se lahko uporabljajo za implementacijo abstraktnih tipov podatkov, kot je npr dinamični nizi, iskalne tabele in prednostne čakalne vrste, in se uporablja v algoritmi za razvrščanje kot je vrsta drevesa.
5. Kakšna je razlika med binarnim iskalnim drevesom in binarnim drevesom?
Binarno iskalno drevo je drevo, ki sledi določenemu vrstnemu redu za razporeditev elementov, medtem ko binarno drevo ne sledi nobenemu vrstnemu redu.
Povezani članki:
- Uporaba BST
- Aplikacije, prednosti in slabosti binarnega iskalnega drevesa
- Vstavljanje v binarno iskalno drevo (BST)
- Iskanje v binarnem iskalnem drevesu (BST)
- Brisanje v binarnem iskalnem drevesu (BST)
