Primer 1:
Oblikujte NFA za prehodno tabelo, kot je navedeno spodaj:
| Sedanje stanje | 0 | 1 |
|---|---|---|
| →q0 | q0, q1 | q0, q2 |
| q1 | q3 | e |
| q2 | q2, q3 | q3 |
| → q3 | q3 | q3 |
rešitev:
Diagram prehoda lahko narišete s funkcijo preslikave, kot je podana v tabeli.
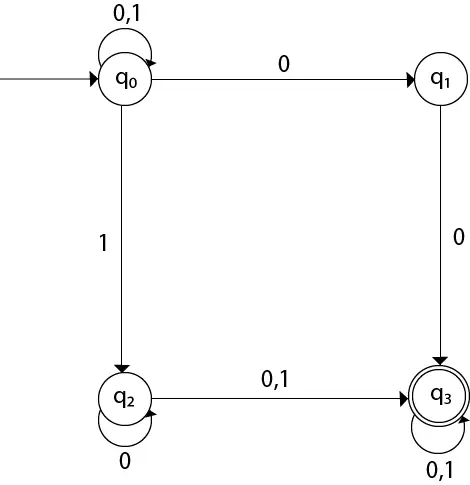
tukaj,
δ(q0, 0) = {q0, q1} δ(q0, 1) = {q0, q2} Then, δ(q1, 0) = {q3} Then, δ(q2, 0) = {q2, q3} δ(q2, 1) = {q3} Then, δ(q3, 0) = {q3} δ(q3, 1) = {q3} Primer 2:
Oblikujte NFA z ∑ = {0, 1} sprejme vse nize, ki se končajo z 01.
e r primeri modelov
rešitev:

Torej bi bil NFA:

Primer 3:
Oblikujte NFA z ∑ = {0, 1}, v katerem dvojnemu '1' sledi dvojni '0'.
rešitev:
združevanje javanskih nizov
FA z dvojnim 1 je naslednji:

Takoj mu mora slediti dvojna 0.
potem,

Pred dvojno 1 je lahko kateri koli niz 0 in 1. Podobno je lahko za dvojno 0 kateri koli niz 0 in 1.
Tako NFA postane:
upravitelj opravil za linux

Zdaj upoštevamo niz 01100011
q0 → q1 → q2 → q3 → q4 → q4 → q4 → q4
Primer 4:
Oblikujte NFA, v katerem vsi nizi vsebujejo podniz 1110.
rešitev:
Jezik je sestavljen iz celotnega niza, ki vsebuje podniz 1010. Diagram delnega prehoda je lahko:

Ker je 1010 lahko podniz. Zato bomo dodali vhodne vrednosti 0 in 1, da bo mogoče ohraniti podniz 1010 jezika. Tako NFA postane:
len niza v Javi

Tabela prehodov za zgornji diagram prehodov je podana spodaj:
| Sedanje stanje | 0 | 1 |
|---|---|---|
| →q1 | q1 | q1, q2 |
| q2 | q3 | |
| q3 | q4 | |
| q4 | q5 | *q5 | q5 | q5 |
Razmislite o nizu 111010,
δ(q1, 111010) = δ(q1, 1100) = δ(q1, 100) = δ(q2, 00)
Obtičala! Ker ni poti od q2 za vhodni simbol 0. Niz 111010 lahko obdelamo na drug način.
δ(q1, 111010) = δ(q2, 1100) = δ(q3, 100) = δ(q4, 00) = δ(q5, 0) = δ(q5, ε)
Kot stanje q5 je sprejemljivo stanje. Dobimo popolno skeniranje in pridemo do končnega stanja.
Primer 5:
Oblikovanje NFA z ∑ = {0, 1} sprejme vse nize, v katerih je tretji simbol z desnega konca vedno 0.
10 od 10
rešitev:

Tako dobimo tretji simbol z desnega konca kot vedno '0'. NFA je lahko:

Zgornja slika je NFA, ker lahko v stanju q0 z vnosom 0 preidemo v stanje q0 ali q1.
