Na začetku glede na prazen komplet in številne poizvedbe na njem, vsaka po možnosti od naslednjih vrst:
- Vstavite 'X' izvedeno s posodobitvijo (1 0 10^6 x 1). Upoštevajte, da je korenina drevesa indeks začetka prenesena kot 0 in končni indeks kot 10^6, tako da se vsi razponi X posodabljajo.
- Delete 'X' se izvede s posodobitvijo (1 0 10^6 x -1). Upoštevajte, da je korenina drevesa indeks začetka prenesena kot 0 in končni indeks kot 10^6, tako da se vsi razponi X posodabljajo.
Primer:
Input : Insert 1 Insert 4 Insert 7 Median Output : The first three queries should insert 1 4 and 7 into an empty set. The fourth query should return 4 (median of 1 4 7).
Za ekspozitorijski namen predpostavljamo naslednje, vendar te predpostavke niso omejitve metode, ki je bila obravnavana tukaj:
1. V vsakem primeru so vsi elementi različni, ki se ne pojavljajo več kot enkrat.
2. "Srednja" poizvedba je narejena le, če je v nizu neparnega števila elementov. (Na našem segmentnem drevesu bomo morali v primeru enakomernih številk narediti dve poizvedbi)
3. Elementi v nizu segajo od 1 do +10^6.
Metoda 1 (naivna)
Pri naivni izvedbi lahko opravimo prvi dve poizvedbi v O (1), vendar zadnjo poizvedbo v O (max_elem), kjer je max_elem največji element vseh časov (vključno z izbrisanimi elementi).
Predpostavimo matriko štetje [] (velikosti 10^6 + 1) za vzdrževanje števila vsakega elementa v podskupini. Sledijo preprosti in samoumevni algoritmi za 3 poizvedbe:
Vstavite x poizvedbo:
count[x]++; if (x > max_elem) max_elem = x; n++;
Izbriši x poizvedbo:
if (count[x] > 0) count[x]--; n--;
Srednja poizvedba:
sum = 0; i = 0; while( sum <= n / 2 ) { i++; sum += count[i]; } median = i; return median; Ilustracija štetja matrike [], ki predstavlja niz {1 4 7 8 9} Srednji element je '7':

"Srednja" poizvedba namerava najti (n + 1)/2 Th "1" v matriki v tem primeru 3. 1 "; Zdaj to storimo z segmentnim drevesom.
Metoda 2 (z uporabo Segmentno drevo )
Naredimo a segmentno drevo Shranjevanje vsote intervalov, kjer interval [a b] predstavlja število elementov, ki so prisotni v kompletu, ki je trenutno v območju [A B]. Na primer, če upoštevamo zgornjo primer poizvedbe (3 7) Vrne 2 Poizvedba (4 4) Vrne 1 poizvedbo (5 5) Vrne 0.
Vstavite in brisanje poizvedb sta preprosta in oboje je mogoče izvesti s posodobitvijo funkcij (int x int diff) (dodaja "difer" pri indeksu "x")
Algoritem
// adds ‘diff’ at index ‘x’ update(node a b x diff) // If leaf node If a == b and a == x segmentTree[node] += diff // If non-leaf node and x lies in its range If x is in [a b] // Update children recursively update(2*node a (a + b)/2 x diff) update(2*node + 1 (a + b)/2 + 1 b x diff) // Update node segmentTree[node] = segmentTree[2 * node] + segmentTree[2 * node + 1]
Zgornja rekurzivna funkcija poteka O (dnevnik (max_elem)) (V tem primeru je max_elem 10^6) in se uporablja za vstavljanje in brisanje z naslednjimi klici:
Zdaj je funkcija, da najdete indeks s Kth '1', kjer bo v tem primeru vedno (n + 1) / 2, to bo delovalo podobno kot binarno iskanje.
Vzemimo primer, da razumemo, da ima naš nabor trenutno elemente {1 4 7 8 9} in je zato predstavljeno z naslednjim segmentnim drevesom.
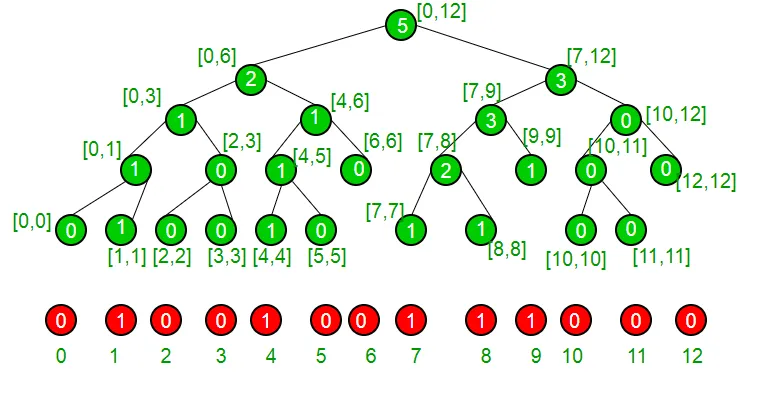
Če smo na vozlišču, ki ni listo, smo prepričani, da imata oba otroka, vidimo, ali ima levi otrok več ali enakega števila enega kot "K", če je da, smo prepričani, da je naš indeks v levi podreji, če ima levo podrejo manjše število 1 kot k, potem smo prepričani, da je naš indeks v desnem podtreju. To naredimo rekurzivno, da dosežemo svoj indeks in od tam ga vrnemo.
Algoritem
1.findKth(node a b k) 2. If a != b 3. If segmentTree[ 2 * node ] >= k 4. return findKth(2*node a (a + b)/2 k) 5. else 6. return findKth(2*node + 1 (a + b)/2 + 1 b k - segmentTree[ 2 * node ]) 7. else 8. return a
Zgornja rekurzivna funkcija poteka O (dnevnik (max_elem)) .
// A C++ program to implement insert delete and // median queries using segment tree #include
// A Java program to implement insert delete and // median queries using segment tree import java.io.*; class GFG{ public static int maxn = 3000005; public static int max_elem = 1000000; // A global array to store segment tree. // Note: Since it is global all elements are 0. public static int[] segmentTree = new int[maxn]; // Update 'node' and its children in segment tree. // Here 'node' is index in segmentTree[] 'a' and // 'b' are starting and ending indexes of range stored // in current node. // 'diff' is the value to be added to value 'x'. public static void update(int node int a int b int x int diff) { // If current node is a leaf node if (a == b && a == x ) { // Add 'diff' and return segmentTree[node] += diff; return ; } // If current node is non-leaf and 'x' // is in its range if (x >= a && x <= b) { // Update both sub-trees left and right update(node * 2 a (a + b) / 2 x diff); update(node * 2 + 1 (a + b) / 2 + 1 b x diff); // Finally update current node segmentTree[node] = segmentTree[node * 2] + segmentTree[node * 2 + 1]; } } // Returns k'th node in segment tree public static int findKth(int node int a int b int k) { // Non-leaf node will definitely have both // children; left and right if (a != b) { // If kth element lies in the left subtree if (segmentTree[node * 2] >= k) { return findKth(node * 2 a (a + b) / 2 k); } // If kth one lies in the right subtree return findKth(node * 2 + 1 (a + b) / 2 + 1 b k - segmentTree[node * 2]); } // If at a leaf node return the index it stores // information about return (segmentTree[node] != 0) ? a : -1; } // Insert x in the set public static void insert(int x) { update(1 0 max_elem x 1); } // Delete x from the set public static void delete(int x) { update(1 0 max_elem x -1); } // Returns median element of the set // with odd cardinality only public static int median() { int k = (segmentTree[1] + 1) / 2; return findKth(1 0 max_elem k); } // Driver code public static void main(String[] args) { insert(1); insert(4); insert(7); System.out.println('Median for the set {147} = ' + median()); insert(8); insert(9); System.out.println('Median for the set {14789} = ' + median()); delete(1); delete(8); System.out.println('Median for the set {479} = ' + median()); } } // This code is contributed by avanitrachhadiya2155
# A Python3 program to implement insert delete and # median queries using segment tree maxn = 3000005 max_elem = 1000000 # A global array to store segment tree. # Note: Since it is global all elements are 0. segmentTree = [0 for i in range(maxn)] # Update 'node' and its children in segment tree. # Here 'node' is index in segmentTree[] 'a' and # 'b' are starting and ending indexes of range stored # in current node. # 'diff' is the value to be added to value 'x'. def update(node a b x diff): global segmentTree # If current node is a leaf node if (a == b and a == x ): # add 'diff' and return segmentTree[node] += diff return # If current node is non-leaf and 'x' is in its # range if (x >= a and x <= b): # update both sub-trees left and right update(node * 2 a (a + b)//2 x diff) update(node * 2 + 1 (a + b)//2 + 1 b x diff) # Finally update current node segmentTree[node] = segmentTree[node * 2] + segmentTree[node * 2 + 1] # Returns k'th node in segment tree def findKth(node a b k): global segmentTree # non-leaf node will definitely have both # children left and right if (a != b): # If kth element lies in the left subtree if (segmentTree[node * 2] >= k): return findKth(node * 2 a (a + b)//2 k) # If kth one lies in the right subtree return findKth(node * 2 + 1 (a + b)//2 + 1 b k - segmentTree[node * 2]) # if at a leaf node return the index it stores # information about return a if (segmentTree[node]) else -1 # insert x in the set def insert(x): update(1 0 max_elem x 1) # delete x from the set def delete(x): update(1 0 max_elem x -1) # returns median element of the set with odd # cardinality only def median(): k = (segmentTree[1] + 1) // 2 return findKth(1 0 max_elem k) # Driver code if __name__ == '__main__': insert(1) insert(4) insert(7) print('Median for the set {147} ='median()) insert(8) insert(9) print('Median for the set {14789} ='median()) delete(1) delete(8) print('Median for the set {479} ='median()) # This code is contributed by mohit kumar 29
// A C# program to implement insert delete // and median queries using segment tree using System; class GFG{ public static int maxn = 3000005; public static int max_elem = 1000000; // A global array to store segment tree. // Note: Since it is global all elements are 0. public static int[] segmentTree = new int[maxn]; // Update 'node' and its children in segment tree. // Here 'node' is index in segmentTree[] 'a' and // 'b' are starting and ending indexes of range stored // in current node. // 'diff' is the value to be added to value 'x'. public static void update(int node int a int b int x int diff) { // If current node is a leaf node if (a == b && a == x) { // Add 'diff' and return segmentTree[node] += diff; return ; } // If current node is non-leaf and 'x' // is in its range if (x >= a && x <= b) { // Update both sub-trees left and right update(node * 2 a (a + b) / 2 x diff); update(node * 2 + 1 (a + b) / 2 + 1 b x diff); // Finally update current node segmentTree[node] = segmentTree[node * 2] + segmentTree[node * 2 + 1]; } } // Returns k'th node in segment tree public static int findKth(int node int a int b int k) { // Non-leaf node will definitely have both // children; left and right if (a != b) { // If kth element lies in the left subtree if (segmentTree[node * 2] >= k) { return findKth(node * 2 a (a + b) / 2 k); } // If kth one lies in the right subtree return findKth(node * 2 + 1 (a + b) / 2 + 1 b k - segmentTree[node * 2]); } // If at a leaf node return the index it // stores information about if (segmentTree[node] != 0) { return a; } else { return -1; } } // Insert x in the set public static void insert(int x) { update(1 0 max_elem x 1); } // Delete x from the set public static void delete(int x) { update(1 0 max_elem x -1); } // Returns median element of the set // with odd cardinality only public static int median() { int k = (segmentTree[1] + 1) / 2; return findKth(1 0 max_elem k); } // Driver code static public void Main() { insert(1); insert(4); insert(7); Console.WriteLine('Median for the set {147} = ' + median()); insert(8); insert(9); Console.WriteLine('Median for the set {14789} = ' + median()); delete(1); delete(8); Console.WriteLine('Median for the set {479} = ' + median()); } } // This code is contributed by rag2127
<script> // A Javascript program to implement insert delete and // median queries using segment tree let maxn = 3000005; let max_elem = 1000000; // A global array to store segment tree. // Note: Since it is global all elements are 0. let segmentTree = new Array(maxn); for(let i=0;i<maxn;i++) { segmentTree[i]=0; } // Update 'node' and its children in segment tree. // Here 'node' is index in segmentTree[] 'a' and // 'b' are starting and ending indexes of range stored // in current node. // 'diff' is the value to be added to value 'x'. function update(nodeabxdiff) { // If current node is a leaf node if (a == b && a == x ) { // Add 'diff' and return segmentTree[node] += diff; return ; } // If current node is non-leaf and 'x' // is in its range if (x >= a && x <= b) { // Update both sub-trees left and right update(node * 2 a Math.floor((a + b) / 2) x diff); update(node * 2 + 1 Math.floor((a + b) / 2) + 1 b x diff); // Finally update current node segmentTree[node] = segmentTree[node * 2] + segmentTree[node * 2 + 1]; } } // Returns k'th node in segment tree function findKth(nodeabk) { // Non-leaf node will definitely have both // children; left and right if (a != b) { // If kth element lies in the left subtree if (segmentTree[node * 2] >= k) { return findKth(node * 2 a Math.floor((a + b) / 2) k); } // If kth one lies in the right subtree return findKth(node * 2 + 1 Math.floor((a + b) / 2) + 1 b k - segmentTree[node * 2]); } // If at a leaf node return the index it stores // information about return (segmentTree[node] != 0) ? a : -1; } // Insert x in the set function insert(x) { update(1 0 max_elem x 1); } // Delete x from the set function delet(x) { update(1 0 max_elem x -1); } // Returns median element of the set // with odd cardinality only function median() { let k = (segmentTree[1] + 1) / 2; return findKth(1 0 max_elem k); } // Driver code insert(1); insert(4); insert(7); document.write('Median for the set {147} = ' + median()+'
'); insert(8); insert(9); document.write('Median for the set {14789} = ' + median()+'
'); delet(1); delet(8); document.write('Median for the set {479} = ' + median()+'
'); // This code is contributed by unknown2108 </script>
Izhod:
Median for the set {147} = 4 Median for the set {14789} = 7 Median for the set {479} = 7
Zaključek:
Vse tri poizvedbe tečejo O (dnevnik (max_elem)) V tem primeru je max_elem = 10^6 SO log (max_elem) približno enak 20.
Segmentno drevo uporablja O (max_elem) prostor.
Če poizvedba izbrisa ni bila, bi bila težava mogoče storiti tudi z znanim algoritmom tukaj .
