Pospešek je sprememba hitrosti s časom. V realnem življenju se tudi pospešek spreminja s časom. Na primer, potujete iz enega mesta v drugo po cesti. Potem boste v tem primeru bolj pospešili v primeru prazne ceste in pospešili navzdol v primeru prometa. To spremembo pospeška lahko opazujemo tako, da na grafu narišemo pospešek glede na čas. To se imenuje časovni graf pospeška. V tem članku se bomo podrobno seznanili s časovnim grafom pospeška in na njegovi podlagi reševali probleme.

numpy dnevnik

Kaj je časovni graf pospeška?

Graf pospešek-čas se uporablja za prikaz razmerja med pospešek in čas, kjer je pospešek neodvisna spremenljivka, prikazana na osi Y, čas pa je odvisna spremenljivka, prikazana na osi X. Dobimo ga, ko dobljene podatke o pospešku in času narišemo na pravokoten graf med preučevanjem gibanja telesa. S pomočjo grafa pospešek-čas lahko določimo spremembo hitrosti v določenem časovnem intervalu. Z določitvijo površine pod krivuljo grafa pospešek-čas lahko ugotovimo spremembo hitrosti gibajočega se telesa v določenem obdobju.

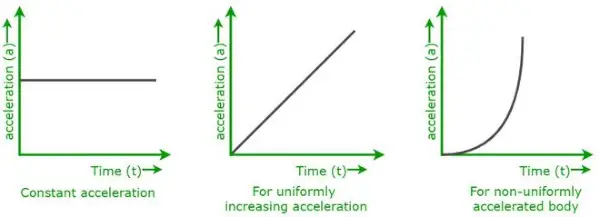
Zgoraj prikazani grafi so grafi pospeška in časa za različne vrste gibanja telesa.

1. Ko se telo giblje s stalnim pospeškom,
2. Ko se telo giblje enakomerno z naraščajočim pospeškom.
3. Ko se telo giblje neenakomerno s spremenljivim pospeškom.

Sklepi

Sledijo točke, ugotovljene iz grafov pospešek-čas.

• Naklon grafa pospešek-čas je △a/△t.
• Območje pod grafom pospešek-čas predstavlja spremembo hitrosti.

Pustiti,

△v biti sprememba hitrosti,

△a biti sprememba pospeška,

△t biti sprememba v času.

zdaj, površina pod krivuljo = △v

Vemo, da se pospešek telesa imenuje stopnja spremembe hitrosti v določenem časovnem obdobju.

Torej,

△a = △v/△t

Z množenjem z △t na obeh straneh dobimo,

△v = △a × △t (v hich je površina pod krivuljo v času pospeška graf )

• Za predmet, ki se giblje s konstantnim pospeškom, je pospešek enak v vseh časovnih intervalih. Zato je naklon grafa pospešek-čas enak nič, graf pa bo vzporeden s časovno osjo.

Pospešek proti zaostanku

Pospešek: Pospešek telesa se imenuje stopnja spremembe hitrosti v določenem časovnem obdobju. Je vektorska količina in se meri v m/s².

Pospešek = sprememba hitrosti/časa

tukaj je sprememba hitrosti pozitivna.

Predpostavimo, da telo, ki potuje z enakomerno hitrostjo, povečuje svojo hitrost. Hitrost povečanja hitrosti imenujemo pospešek telesa. Naj bo u začetna hitrost, v končna hitrost in t časovni interval, potem je pospešek telesa podan kot

Pospešek (a) = (v – u)/t

primer: Primer pospeševanja v vsakdanjem življenju je zavijanje avtomobila v ovinku. Hitrost avtomobila se poveča s spremembo smeri, kar povzroči pospešek. Pospešek se poveča z naraščajočo hitrostjo vrtenja.

Zaostalost: Zaostajanje telesa se imenuje stopnja spremembe hitrosti v določenem časovnem obdobju. Retardacija pomeni negativni pospešek.

Zaostajanje = sprememba hitrosti/časa

tukaj je sprememba hitrosti negativna.

Predpostavimo, da telo, ki potuje z enakomerno hitrostjo, zmanjšuje svojo hitrost. Hitrost zmanjševanja hitrosti imenujemo retardacija telesa. Naj bo u začetna hitrost, v končna hitrost in t časovni interval, potem je zaostanek telesa podan kot

Zaostalost = (v – u)/t

primer: Primer retardacije iz resničnega življenja je izklop ventilatorja. Ko je stikalo premikajočega se ventilatorja izklopljeno, se hitrost vrtenja lopatic ventilatorja postopno upočasni. Ta stopnja zmanjšanja hitrosti ventilatorja je znana kot upočasnitev.

Preverite tudi to:

• Grafi razdalje in časa
• Časovni grafi hitrosti

Vzorci problemov na časovnih grafih pospeška

1. naloga: Iz spodnjega grafa pospeška in časa določite spremembo hitrosti.

rešitev:

Da bi našli spremembo hitrosti telesa, moramo določiti površino pod krivuljo.

Torej, da bi ugotovili spremembo hitrosti predmeta, moramo izračunati površino trikotnika.

△v = površina trikotnika

= ½ × 25 × 6

△v = 75 m/s.

Zato je sprememba hitrosti 75 m/s.

2. naloga: Iz spodnjega grafa pospeška in časa poiščite začetno hitrost telesa, če je njegova končna hitrost 55 m/s.

rešitev:

Da bi našli spremembo hitrosti telesa, moramo določiti površino pod krivuljo. Iz grafa lahko opazimo, da ima pravokotnik in trikotnik. Torej, da bi ugotovili spremembo hitrosti predmeta, moramo izračunati površino teh številk.

△v = ploščina trikotnika + ploščina pravokotnika

= ½ × 8 × 6 + 2 × 8

△v = 24 + 16 = 42 m/s

Vemo, da

△v = končna hitrost – začetna hitrost

42 = 55 – in_jaz

v_jaz= 55 – 42 = 13 m/s

Zato je začetna hitrost 13 m/s.

Problem 3: Iz spodnjega grafa pospeška v odvisnosti od časa določite hitrost pri t = 6 s, če je v(0) = 0.

rešitev:

Pospešek daje;

a = dv/dt

⇒ dv = (a)dt

Z integracijo na obeh straneh dobimo

∫dv = ∫(a) dt

⇒ v = ∫(1,5) dt

⇒ v(t) = 1,5t + c, kjer je c konstanta

⇒ v(0) = 0

⇒ c = 0

Zdaj je v(t) = 1,5t

v(6) = 1,5 × 6 = 9 m/s

Zato je hitrost pri t = 6 s 9 m/s.

Problem 4: Kaj kaže površina pod grafom pospešek-čas?

rešitev:

Območje pod grafom pospešek-čas predstavlja spremembo hitrosti.

Naj bo △v sprememba hitrosti, △a sprememba pospeška in △t sprememba časa.

Zdaj je površina pod krivuljo = △v

Vemo, da se pospešek telesa imenuje razmerje med spremembo hitrosti v določenem časovnem obdobju.

Torej,

△a = △v/△t

Z množenjem z △t na obeh straneh dobimo,

△v = △a × △t

Torej površino pod krivuljo dobimo tako, da pomnožimo spremembo pospeška in spremembo časa.

Problem 5: Kaj pomeni sunek v časovnem grafu pospeška?

rešitev:

Sunek je nenadna sprememba pospeška premikajočega se telesa, naklon grafa a-t pa predstavlja sunek.

Naklon grafa pospešek-čas = sunek = △a/△t

Časovni graf pospeška – pogosta vprašanja

Kaj je graf pospešek-čas?

Graf pospešek-čas prikazuje, kako se pospešek skozi čas spreminja za predmet, ki se premika v ravni liniji. Nariše pospešek na osi y glede na čas na osi x.

Kako izračunate površino pod grafom pospešek-čas in kaj predstavlja?

Območje pod grafom pospešek-čas predstavlja spremembo hitrosti v časovnem obdobju, ki ga zajema graf. Za izračun te površine bi običajno sešteli površine pravokotnikov ali trapezov, ki se prilegajo pod krivuljo, ki ustrezajo različnim časovnim intervalom, v katerih je pospešek konstanten.

Ali lahko določite hitrost predmeta v določenem času iz grafa pospešek-čas?

Neposredna določitev trenutne hitrosti v določenem času iz grafa pospešek-čas ni mogoča. Lahko pa izračunate spremembo hitrosti v določenem časovnem obdobju tako, da poiščete površino pod grafom znotraj tega obdobja. Če poznate začetno hitrost, lahko določite končno hitrost.

Kaj pomeni negativni pospešek na tej vrsti grafa?

Negativni pospešek na grafu pospešek-čas označuje pojemek, kjer se hitrost predmeta zmanjša, če se predmet premika v pozitivni smeri. Če se predmet premika v smeri, ki velja za negativno, potem negativni pospešek pomeni povečanje hitrosti.

Kako lahko najdete povprečni pospešek iz grafa pospešek-čas?

Povprečni pospešek je mogoče določiti tako, da se ugotovi skupna sprememba hitrosti (sešteje se površina pod krivuljo, upošteva smer) in se deli s skupnim časovnim intervalom. Vizualno je to mogoče predstaviti kot pravokotnik, katerega površina je enakovredna skupni površini pod grafom pospešek-čas.

Kaj predstavlja naklon grafa pospešek-čas?

Naklon grafa pospešek-čas označuje stopnjo spremembe pospeška skozi čas, ki je znana kot sunek. Strm klanec pomeni hitro spremembo pospeška.

Kako predstavljate telo v mirovanju na grafu pospešek-čas?

Telo, ki miruje ali se giblje s konstantno hitrostjo, je na grafu pospešek-čas predstavljeno s črto vzdolž časovne osi pri ničelnem pospešku.

Kako si razlagate graf pospešek-čas?

Naklon grafa pospešek-čas predstavlja stopnjo spremembe pospeška, pri čemer strmejši naklon kaže višjo stopnjo spremembe.

Kaj predstavlja površina pod grafom pospešek-čas?

Območje pod krivuljo na grafu pospešek-čas predstavlja spremembo hitrosti predmeta. Natančneje, predstavlja končno hitrost minus začetno hitrost.