Ničele polinoma so tiste dejanske, namišljene ali kompleksne vrednosti, če jih damo v polinom namesto spremenljivke, rezultat postane nič (kot nakazuje tudi ime). Polinomi se uporabljajo za modeliranje nekaterih fizičnih pojavov, ki se dogajajo v resničnem življenju, in so zelo uporabni pri matematičnem opisovanju situacij.

Ničle polinoma so vse vrednosti x, zaradi katerih je polinom enak nič. Ničle polinoma nam povedo o x-presretkih grafa polinoma. V tem članku bomo razpravljali o ničle polinoma, kako jih najti, faktorski izrek itd.

Kazalo

• Kaj so ničle polinomov?
• Ničle polinomske formule
• Kako najti ničlo polinoma?
• Za linearni polinom
• Za kvadratni polinom
• Za kubični polinom
• Faktorski izrek
• Razmerje med ničlami ​​in koeficientom
• Povezava med ničlami ​​in koeficientom za kvadratno enačbo
• Povezava med ničlami ​​in koeficientom za kubično enačbo
• Sestavljanje enačbe z ničlami ​​polinoma
• Ničle v grafu polinomov
• Temeljni izrek linearne algebre
• Večkratnost korena
• Članki, povezani z ničlami ​​polinoma
• Vzorci nalog o ničlah polinoma
• Vadbene naloge na ničlah polinoma

Kaj so ničle polinomov?

Za polinom P(x) pravimo, da je x = a nič polinoma, če je P(a) = 0, vse take ničle polinoma pa običajno imenujemo ničle polinoma. Na primer, upoštevajte f(x) = 3x – 12. Sedaj pa v polinom vnesite x = 4, tj. f(4) = 3×4 – 12 = 0. Tako je x = 4 nič polinoma f( x) = 3x – 12.

Primer: Za f(x) = x ³ – 6x ² + 11x – 6, ali je x = 1 nič?

rešitev:

Če želite preveriti, ali je x = 1 nič od f(x) = x³– 6x²+ 11x – 6 ali ne, postavite x = 1 v (x)

f(1) = (1)³– 6×(1)²+ 11×(1) – 6

⇒ f(1) = 1 – 6 + 11 – 6 = 12 -12 = 0

Tako je x = 1 ničla od f(x).

Ničle polinomske formule

Za linearni polinom oblike ax + b je njegova ničla podana z x = -b/a.

Za kvadratni polinom oblike ax²+ bx + c, njegova ničla je podana z x = {- b ± √D}/2a, kjer je D diskriminanta, podana z b²– 4ac.

Kako najti ničlo polinoma?

Ničle polinoma lahko najdemo za različne vrste polinomov z različnimi metodami, ki so obravnavane spodaj.

• Za linearni polinom
• Za kvadratni polinom
• Za kubični polinom

Za linearni polinom

Pri linearnih polinomih je najlažje najti nič. saj obstaja samo ena ničla in to je mogoče izračunati tudi s preprosto preureditvijo polinoma za enačajnim polinomom na 0.

Na primer, poiščite ničlo za linearni polinom f(x) = 2x – 7.

rešitev:

Če želite najti nič od f(x), enačite f(x) z 0.

⇒ 2x – 7 = 0

⇒ 2x = 7

⇒ x = 7/2

Za kvadratni polinom

Obstajajo različne metode za iskanje korenin ali ničel kvadratnega polinoma, kot je razdelitev srednjega člena, kvadratna formula, ki je znana tudi kot formula Shree Dharacharya, in dokončanje kvadrata, ki je nekoliko podoben kvadratni formuli, saj je kvadratna formula iz dokončanja kvadrata za splošno kvadratno enačbo.

Izvedite več o reševanje kvadratnih enačb ali polinome in kako jih rešiti. Naslednji primeri podrobno prikazujejo metodo za iskanje ničel kvadratnih polinomov.

Primer 1: Poiščite ničle za P(x) = x ² + 2x – 15.

odgovor:

x²+ 2x – 15 = 0

⇒ x²+ 5x – 3x – 15 = 0

⇒ x(x + 5) – 3(x + 5) = 0

⇒ (x – 3) (x + 5) = 0

⇒ x = 3, -5

Primer 2: Poiščite izhodne ničle za P(x) = x ² – 16x + 64.

odgovor:

x²– 16x + 64 = 0

Primerjava s sekiro²+ bx + c = 0,

dobimo a = 1, b = -16 in c = 64.

torej

⇒ x = 8, 8

Za kubični polinom

Če želite najti ničle kubika, obstaja veliko načinov, na primer izrek o racionalnem korenu in dolgo deljenje skupaj. Eden od načinov iskanja korenin kubičnega polinoma ali polinoma višje stopnje je naslednji:

Korak 1: Za iskanje možnih korenin uporabite izrek o racionalnem korenu. tj. Če ima polinom racionalen koren, mora biti to deljenje p/q, kjer je p celoštevilska konstanta in q vodilni koeficient.

2. korak: Ko najdete en koren, delite polinom s faktorjem, ki ga tvori ta koren, z dolgim ​​deljenjem in zapišite polinom kot produkt količnika in dividende.

3. korak: Če je kvocient kvadratni izraz, ga rešite z zgoraj omenjenimi metodami za kvadratne polinome. Če ni polinom stopnje 2, ponavljajte koraka 1 in 2, dokler količnik ne postane polinom stopnje 2.

4. korak: Rezultat 3. koraka so zahtevani faktorji in z enačenjem faktorja z 0 lahko najdemo ničle polinoma.

Primer: Poiščite ničle kubičnega polinoma p(x) = x ³ + 2x ² – 5x – 6.

rešitev:

p(x) = x³+ 2x²– 5x – 6

Kot p/q = -6

Po izreku o racionalnem korenu so vse možne racionalne korenine polnoma delitelji p/q.

Tako so delilci = ±1, ±2, ±3, ±6

x = -1, v p(x), dobimo

p(-1) = (-1)³+ 2(-1)²– 5(-1) – 6

⇒ p(-1) = -1 + 2 + 5 – 6 = 0

Tako je po faktorskem izreku x + 1 faktor p(x).

Tako je x³+ 2x²– 5x – 6 = (x+1)(x²+x – 6)

⇒ x³+ 2x²– 5x – 6 = (x+1)(x-2)(x+3)

Za ničle je p(x) = 0,

Ničele p(x) so x = -1, x = 2 in x = -3.

Faktorski izrek

Za polinom P(x) faktorski izrek pravi, da če je x =a nič od P(X), če je x – a faktor od P(x). to pomeni, da morata veljati oba naslednja pogoja.

• Če je a nič P(x), potem bo x−a faktor P(x)
• Če je x−a faktor P(x), potem bo a nič P(x)

To lahko preverimo z ogledom prejšnjih primerov. Faktorski izrek lahko vodi do nekaj zanimivih rezultatov, ki so naslednji:

Rezultat 1: Če je P(x) polinom stopnje n in je r ničla od P(x), potem lahko P(x) zapišemo v naslednji obliki,

P(x) = (x – r) Q(x)

Pri čemer je Q(x) polinom stopnje n-1 in ga lahko ugotovimo tako, da P(x) delimo z (x – r).

Rezultat 2: Če je P(x) = (x-r)Q(x) in je x = t nič od Q(x), potem bo x = t prav tako nič od P(x).

Za potrditev zgornjega dejstva,

Recimo, da je t nič Q(x), kar pomeni Q(t) = 0.

Vemo, da je r ničla polinoma P(x), kjer je P(x) = (x – r) Q(x),

Torej moramo preveriti, ali je x = t tudi nič P(x), vstavimo x = t v P(x)

⇒ P(t) = (t – r) Q(t) = 0

Torej je x = t tudi nič P(x).

Torej, dokazano.

Razmerje med ničlami ​​in koeficientom

Razmerje med ničlami ​​in koeficientom kvadratne in kubične enačbe je obravnavano spodaj.

Povezava med ničlami ​​in koeficientom za kvadratno enačbo

Za kvadratno enačbo oblike ax²+ bx + c = 0, če sta dve ničli kvadratne enačbe α in β, potem

• Vsota korena = α + β = -b/a
• Produkt korenin = α × β = c/a

Povezava med ničlami ​​in koeficientom za kubično enačbo

Če so α, β in γ koren kubičnega polinoma ax³+ bx²+ cx + d = 0, potem je razmerje med njegovimi ničlami ​​in koeficienti podano takole:

• a + b + c = -b/a
• α × β × γ= -d/a
• αβ + αγ + βγ = c/a

Sestavljanje enačbe z ničlami ​​polinoma

• Za kvadratni polinom z ničlama α in β je kvadratni polinom podan z

x ² – (a + b)x + ab .

• Za kubični polinom s tremi ničlami ​​α, β in γ je kubični polinom podan z

x ³ – (a + b + c )x ² + (ab + ag + bg)x – abg

Ničle v grafu polinomov

V grafu katerega koli polinoma y = f(x) so realne ničle točke, pri katerih graf seka ali se dotika osi x. (kot graf z namišljeno ničlo nikoli ne seka osi x). Z drugimi besedami, če obstajajo 3 realne rešitve kubičnega polinoma, potem graf tega kubičnega polinoma trikrat seka os x, če pa obstaja samo ena realna rešitev za nek kubični polinom, potem ta graf samo seka os x enkrat.

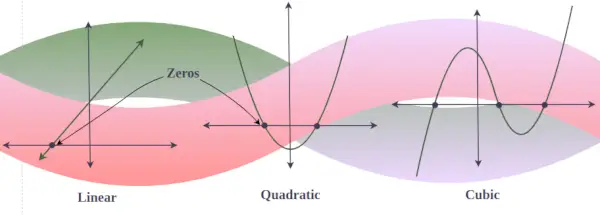
Temeljni izrek linearne algebre

Če je P(x) polinom stopnje n, bo imel P(x) natanko n ničel, od katerih se nekatere lahko ponavljajo.

To pomeni, da če naštejemo vse ničle in vsako naštejemo k-krat, ko je k njena mnogokratnost. Na seznamu bomo imeli točno n številk. To je lahko uporabno, saj nam lahko da predstavo o tem, koliko ničel mora biti v polinomu. Torej lahko prenehamo iskati ničle, ko dosežemo zahtevano število ničel.

Večkratnost korena

Recimo, da imamo polinom P(x) = 0, ki je faktoriziran na

P(x) = (x – r) ^k (x – a) ^m

Če je r nič polinoma in je eksponent na njegovem členu, ki je dal koren, k, potem pravimo, da ima r večkratnost k . Pogosto se imenujejo ničle z množico 1 preprosto ničle in ničle z mnogokratnostjo 2 imenujemo dvojne korenine polinoma.

Primer: P(x) je polinom stopnje 5, ki je bil faktoriziran za vas. Naštej korenine in njihovo mnogoterost.

P(x) = 5x ⁵ −20x ⁴ +5x ³ +50x ² −20x−40=5(x+1) ² (x−2) ³

rešitev:

Podano je P(x) = 5(x+1)²(x−2)³

⇒ P(x) = 5(x+1)(x+1)(x+1)(x−2)(x−2)

Za iskanje ničel je P(x) = 0

⇒ x = -1, -1, 2, 2, 2

Upoštevajte, da se -1 pojavi dvakrat kot ničla, zato je njegova množina 2, medtem ko je večkratnost ničle 2 3.

Članki, povezani z ničlami ​​polinoma

• Polinom
• Korenine kvadratne enačbe
• Algebrski izraz

Vzorci nalog o ničlah polinoma

Problem 1: Če je x = 2 ničla od P(x) = x ³ +2x ² −5x−6. Poiščite drugi dve ničli.

rešitev:

Iz temeljnega izreka, ki smo ga preučevali prej, lahko rečemo, da bo imel P(x) 3 ničle, ker je tristopenjski polinom. Eden od njih je x = 2.

Torej lahko ponovno zapišemo P(x),

P(x) = (x – 2) Q(x)

Da bi našli drugi dve ničli, moramo najti Q(x).

Q(x) lahko ugotovimo tako, da P(x) delimo z (x-2).

niz java vsebuje

Po deljenju je Q(x) enak,

Q(x) = x²+ 4x + 3

Preostali dve ničli lahko razberemo iz tega,

Q(x) = x²+ 3x + x + 3

⇒ x(x + 3) + 1(x + 3)

⇒ (x + 1) (x + 3)

Q(x) = 0,

x = -1, -3

Tako sta drugi dve ničli x = -1 in x = -3.

2. naloga: Glede na to, da je x = r ničla polinoma, poiščite druge ničle polinoma.

P(x) = x ³ -6x ² −16x; r = −2

rešitev:

Vemo, da je x = -2 ničla,

Torej lahko P(x) prepišemo kot P(x) = (x + 2) Q(x) {z uporabo algoritma deljenja}

Zdaj, da bi našli Q(x), naredimo isto stvar kot v prejšnjem vprašanju, delimo P(x) z (x + 2).

Dobimo,

Q(x) = x²– 8x

Zdaj, da bi našli drugi dve ničli, faktorizirajte Q(x)

Q(x) = x (x – 8) = 0

Torej so ničle x = 0, 8.

Tako imamo tri ničle, x = -2, 0, 8.

Problem 3: Poiščite ničle polinoma, 4x ³ -3x ² -25x-6 = 0

rešitev:

Trik za reševanje polinomskih enačb s stopnjo 3,

Poiščite najmanjše celo število, zaradi katerega je lahko polinomska vrednost 0, začnite z 1,-1,2 itd.

ugotovimo, da je za x = -2 vrednost izraza enaka nič.

Zato je ena od korenin -2.

V skladu s faktorskim izrekom, če je a ena od ničel polinoma, je torej (x-a) faktor danega polinoma.

Tako sledi temu {x – (-2)} = (x+2) faktor pof nad polinomom.

Dobimo kvadratno enačbo in ničle so že tam.

(4x²-11x-3)(x+2) = 0

Faktoriziraj kvadratno enačbo,

(4x²-12x+x-3)(x+2) = 0

[4x(x-3)+1(x-3)](x+2) = 0

(4x+1)(x-3)(x+2) = 0

x = -2, x = 3, x = -1/4

Problem 4: Poiščite ničle polinoma, 4x ⁶ – 16x ⁴ = 0

rešitev:

Polinom ima do stopnje 6, zato obstaja 6 ničel polinoma.

4x⁴(x²-4) = 0

4x⁴(x²-2²) = 0

4x⁴[(x+2)(x-2)] = 0

Zato je x = 0, 0, 0, 0, 2, -2

Problem 5: Poiščite ničle polinomske funkcije f(x) = x ³ – 2x ² – 5x + 6

rešitev:

Da bi našli ničle tega polinoma, nastavimo f(x) = 0 in rešimo x:

f(x) = x³– 2x²– 5x + 6 = 0

Kot d/a = 6

Po izreku o racionalnem korenu so vse možne racionalne korenine polnoma:

Delitelji d/a = ±1, ±2, ±3, ±6

x = 1, v p(x), dobimo

f(1) = (1)³– 2 (1)²– 5(1) – 6

f(-1) = 1 – 2 – 5 + 6 = 0

Tako je po faktorskem izreku x – 1 faktor p(x).

Tako je x³+ 2x²– 5x – 6 = (x-1)(x²-x – 6)

x³+ 2x²– 5x – 6 = (x-1)(x+2)(x-3)

Za ničle je p(x) = 0,

Ničele p(x) so x = 1, x = -2 in x = 3.

Vadbene naloge na ničlah polinoma

1. Poiščite vse ničle polinoma f(x) = x ³ – 6x ² + 11x – 6

2. Določite vse ničle polinoma g(x) = 2x ⁴ – 7x ³ + 3x ² + 4x – 4

3. Poiščite ničle polinoma h(x) = x ⁵ – 3x ⁴ + 2x ³ – 6x ² + x + 2

4. Določite vse ničle polinoma p(x) = 3x ⁴ – 16x ³ + 18x ² + 16x – 12.

Pogosta vprašanja o ničlah polinoma

Kaj so ničle polinoma?

Te take realne vrednosti, saj vrednost polinoma postane 0, tj. če je p(x) polinom in je p(a) = 0, potem je x = a nič od p(x).

Kako najti ničle polinoma?

Obstajajo različne metode za različne polinome za iskanje ničel, na primer za kvadratno prelivanje srednjega člena in kvadratne formule. Za linearno, preprosto preureditev spremenljivk in za kubično uporabljamo kombinacijo izreka o racionalnem korenu, dolgega deljenja, izreka o faktorju in izreka o ostankih.

Ali ima lahko polinom več kot eno ničlo?

Da, polinom ima lahko več kot eno ničlo, pravzaprav ima lahko polinom n stopinj največ n realnih ničel.

Kakšna je mnogokratnost ničle polinoma?

V procesu faktorizacije se pojavi en faktor ali ena ničla polinoma, nato pa večkrat faktor ali ničla, kar se imenuje množica tega korena.

Kaj je temeljni izrek algebre?

Temeljni izrek algebre pravi, da če je P(x) polinom stopnje n, potem ima P(x) natanko n ničel, od katerih se nekatere lahko ponavljajo.

Ali ima polinom s stopnjo n vedno n pravih korenin?

Ne, polinom s stopnjo n nima vedno n realnih korenin, saj so lahko nekatere korenine namišljena ali kompleksna števila.

Kaj je stopnja ničelnega polinoma?

Stopnja ničelnega polinoma je nič.