Trapez pri matematiki: Trapez je mnogokotnik s štirimi stranicami, torej je štirikotnik. Trapez izvira iz grške besede trapez, kar pomeni miza. Je kompleksen štirikotnik. Trapez je poseben štirikotnik s samo enim parom vzporednih stranic. Trapez je dvodimenzionalna oblika, ki je videti kot miza.
Trapez ima štiri stranice in štiri oglišča. Trapezno obliko vidimo v vsakdanjem življenju in je ena najpogostejših oblik. V tem članku bomo spoznali kaj je trapez v matematiki, njegove lastnosti, formule, primeri in vrste trapeza ter nekaj rešenih primerov zanj.
Kazalo
- Kaj je trapez v matematiki?
- Vrste trapeza
- Nepravilen trapez
- Lastnosti trapeza
- Trapezna formula
- Območje formule trapeza
- Formula za obseg trapeza
- Razlika med trapezom in trapezom
- Koti trapeza
- Diagonala trapeza
- Primeri trapeza
Kaj je trapez v matematiki?
Trapez je dvodimenzionalni štirikotnik zaprte oblike s parom vzporednih nasprotnih stranic. Vzporedne stranice trapeza imenujemo osnove, nevzporedne stranice trapeza pa noge. Trapez ima štiri stranice in štiri vogale. A paralelogram imenujemo tudi trapez z dvema vzporednima stranicama.
Definicija trapeza
Trapez je štirikotnik (štirikotnik) z vsaj enim parom vzporednih stranic. Te vzporedne stranice imenujemo osnove trapeza, drugi dve strani pa kraki, ki nista nujno vzporedni.
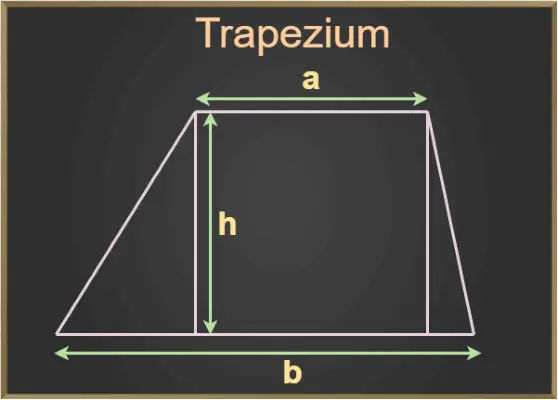
java polje
Na zgornji sliki sta a in b osnovici trapeza, h pa višina trapeza.
Trapezna oblika
Trapez je a štirikotnik tj. mnogokotnik s štirimi stranicami. Trapez ima štiri stranice s parom nasprotnih stranic, ki sta med seboj vzporedna. Trapezna oblika je zelo pogosta in v vsakdanjem življenju vidimo različne stvari, ki so podobne trapezu. Nekateri primeri trapeza v resničnem življenju, ki smo jih opazili, so mize v obliki trapeza, ploščice, slike in drugo.
Vrste trapeza
Glede na stranice in kote je trapez treh vrst:
- skalen trapez
- Enakokraki trapez
- Desni trapez

Enakokraki trapez
Trapez, ki ima enako dolge krake, se imenuje enakokraki trapez, kar pomeni, da sta v enakokrakem trapezu obe strani, ki nista vzporedni, enaki.
skalen trapez
Trapez, katerega stranice niso enake, se imenuje skalen trapez. V skalenskem trapezu ni dveh enakih kotov.
Desni trapez
Trapez, ki ima par pravih kotov, ki mejita drug na drugega, je znan kot pravi trapez.
Nepravilen trapez
Trapez ima en par vzporednih stranic, drugi dve strani pa sta nevzporedni. V pravilnem trapezu sta drugi dve nevzporedni stranici enaki, v primeru nepravilnega trapeza pa sta dve nevzporedni nasprotni stranici neenaki.
Lastnosti trapeza
Obstajajo različne lastnosti trapeza, od katerih so nekatere naslednje:
- Vzporedne stranice: Trapez ima dve vzporedni strani, ki ju imenujemo osnove. primer: Stranici AB in CD sta med seboj vzporedni, kot je prikazano na sliki.
- Nevzporedne stranice: Stranice trapeza, ki niso vzporedne, se imenujejo kraki, kraki trapeza pa niso enako dolgi. primer: Stranici AD in BC sta nevzporedni stranici trapeza.
- Višina ali nadmorska višina: Pravokotna razdalja med bazama se imenuje višina ali nadmorska višina trapeza. V zgornjem diagramu je h višina trapeza.
- Vsota kotov
- Sosednji notranji koti v trapezu znašajo 180°. primer: Obstajata dva para sonotranjih kotov. En par je ∠ A in ∠ D, medtem ko je drugi par ∠ B in ∠ C. Vsota vsakega para sonotranjih kotov je 180°.
- Vsota vseh notranjih kotov v trapezu je vedno 360°. Primer : Na sliki je ∠A+∠D 180° in ∠B+∠C 180°. Zato je ∠A+∠D +∠B+∠C = 360°.
- Mediana: Mediana trapeza je odsek, ki povezuje središča krakov. Mediana je vzporedna z osnovo in njena dolžina je povprečje dolžin osnov.
- Trapez ima natanko en par nasprotnih stranic, ki sta vzporedni.
Trapezna formula
Pomembne formule trapeza so:
- Območje trapeza = ½ (vsota vzporednih stranic) × (razdalja med vzporednima stranicama)
- Obod trapeza = Vsota vseh štirih strani
Območje formule trapeza
Trapez ima dve vzporedni strani enoti a oziroma b, njegova nadmorska višina pa je h.
Zdaj lahko površino trapeza izračunamo tako, da poiščemo povprečje baz in rezultat pomnožimo z nadmorsko višino. torej
Območje trapeza = ((a +b)/2) × h
kje,
- a in b so osnove trapeza
- h je nadmorska višina
Območje enakokrakega trapeza
Naj sta a in b dolžini vzporednih stranic trapeza ABCD, kjer sta a in b osnovici trapeza in a>b.
Ker gre za enakokraki trapez, je c dolžina obeh nevzporednih stranic, h pa višina trapeza.
Zdaj je AB = a, CD = b, BC = AD = c
noter Pravokotni trikotnik , AED
Dolžina pravokotnice, h = √(c 2 – (a-b) 2 ) [uporaba Pitagorov izrek ]….(1)
zdaj,
Ploščina = ½ × vsota vzporednih stranic × višina trapeza
Površina = ½ × (a+b) × h
Uporaba enačbe (1)
Območje enakokrakega trapeza = 1/2 × [√(c 2 – (a-b) 2 ) (a+b)]
Formula za obseg trapeza
Obseg trapeza dobimo z izračunom vsote vseh njegovih stranic. torej
Obseg trapeza = AB + BC + CD + AD
kje, AB, BC, CD in AD so stranice trapeza
Obseg enakokrakega trapeza
Če sta v enakokrakem trapezu a in b dolžini vzporednih stranic, tj. osnov in je c dolžini dveh enakih nevzporednih stranic, potem je obseg podan z:
Obod = a + b + 2c
kje,
- a , b so osnove trapeza
- c je enaka stranica trapeza
Razlika med trapezom in trapezom
Na splošno sta trapez in trapez enaka, razlika pa je v državi izvora.
- Trapez je britanskega izvora, je štiristranski mnogokotnik in dvodimenzionalna figura, ki ima natanko en par vzporednih strani nasproti drug drugemu. V Indiji sledimo britanski angleščini, zato se uporablja beseda Trapezium.
- Trapez je ameriškega izvora, je prav tako štiristranski mnogokotnik z enim parom vzporednih stranic, ki si nasproti stojijo. Vzporedni stranici sta osnovici, drugi dve nevzporedni stranici pa se imenujeta kraka trapeza.
Koti trapeza
Trapez je štirikotnik in vsota vseh kotov štirikotnika je 360 stopinj. Torej je vsota vseh notranjih kotov trapeza 360 stopinj.
Za vsak pravilen trapez je enak tisti trapez, v katerem so nevzporedne stranice enake sosednjim kotom med vzporedno in nevzporedno premico. Tako je vsota teh dveh kotov dopolnilna.
Vzemimo primer za podporo tega koncepta za enakokraki trapez ABCD, če je AB vzporeden s CD in je AD enak CD, potem vemo, da je ∠A = ∠B in ∠C = ∠D, potem,
∠A + ∠B + ∠C + ∠D = 360°
Tukaj je ∠A = ∠B in ∠C = ∠D
∠A + ∠A + ∠C + ∠C = 360°
2(∠A + ∠C) = 360°
(∠A + ∠C) = 180°
Podobno je (∠B + ∠D) = 180°
Diagonala trapeza
Trapez je posebna vrsta štirikotnika; tako ima tudi trapez dve diagonali. Diagonale trapeza nimajo enakih dolžin, za razliko od nekaterih drugih štirikotnikov, kot so pravokotniki ali paralelogrami. Diagonale trapeza nimajo enakih dolžin in so dolžine diagonal odvisne od dolžin osnov in kotov trapeza.
Primer: za enakokraki trapez ABCD je osnovni kot ∠A 80°, nato poiščite drugi kot ∠C.
Vemo, da je za enakokraki trapez ABCD
(∠A + ∠C) = 180°
Podano je ∠A = 80°
Zdaj je 80° + ∠C = 180°
∠C = 180 – 80
∠C = 100°
Tako je zahtevani kot ∠C 100°
Formule za trapez – ploščina in obseg trapeza
Formule, povezane s trapezom, so povzete v naslednji tabeli:
| Lastnina | Formula |
|---|---|
| Območje | 1/2 × ( a + b ) × h |
| Območje (enakokraki trapez) | 1/2 × [√(c2– (a-b)2) (a+b)] |
| Obseg | a + b + c + d |
| Obod (enakokraki trapez) | a + b + 2 c |
| Mediana | (a + b)/2 |
Ljudje preberejo tudi:
kako dobiti apple emojis na android
- Romb
- Trikotnik
- Kakšna je formula za iskanje površine trapeza?
Primeri trapeza
Primer 1: Poišči četrto stranico trapeza, če so ostale tri stranice dolge 8 cm, 12 cm in 16 cm, obseg pa 40 cm.
rešitev:
Obod je podan kot vsota vseh njegovih strani. Naj bo dolžina o neznanka 'x' enot.
Obod = 40
40 = 8 + 12 + 16 + x
x = 40 – (8 + 12 + 16)
= 4 cm
Torej je dolžina neznane stranice 4 cm
Primer 2: Trapez ima vzporedni stranici dolžine 15 cm in 11 cm ter nevzporedni stranici dolžini 5 cm. Izračunajte obseg trapez.
rešitev:
To je enakokraki trapez, ker je jasno omenjeno, da sta nevzporedni stranici, dolgi 5 cm, enaki.
Glede na enakokraki trapez, če sta dve nevzporedni strani trapeza enako dolgi, je znan kot enakokraki trapez.
podano,
- a = 15 cm
- b = 11 cm
- c = 5 cm
Obod = a + b + 2c
P = 15 + 11 + 2 (5)
P = 15 + 11 + 10
P = 36 cm
Primer 3: Poiščite obseg trapeza s stranicami 12 cm, 14 cm, 16 cm in 18 cm.
rešitev:
P = vsota vseh strani
P = 12 + 14 + 16 + 18
P = 60 cm
Obseg trapeza je torej 60 cm
Primer 4: Poiščite ploščino trapeza, katerega vsota vzporednih stranic je 60 cm, njegova višina pa 10 cm.
rešitev:
podano,
- Vsota vzporednih stranic 60 cm
- višina, v = 10 cm
Ploščina trapeza, A = 1/2 × vsota vzporednih stranic × razdalja med vzporednima stranicama
Zamenjava danih vrednosti,
A =1/2×60×10
A = 30×10
A = 300 cm2
Zato je površina trapeza = 300 cm2
Vadbene naloge na trapezu pri matematiki
1. Poišči ploščino trapeza z osnovama 10 cm in 15 cm ter višino 6 cm.
2. Trapez ima površino 54 kvadratnih metrov. Če je ena od osnov dolga 12 metrov in je višina 6 metrov, poiščite dolžino druge baze.
3. Izračunaj obseg trapeza z osnovama 8 cm in 14 cm ter nevzporednima stranicama 5 cm in 7 cm.
4. Določi dolžino sredinca v trapezu, katerega osnovnici merita 18 cm in 30 cm.
5. V enakokrakem trapezu sta kota pri eni osnovi 45 stopinj. Poiščite mere kotov pri drugi osnovi. Predpostavimo, da trapez ni pravi trapez.
Povzetek – Trapez v matematiki
Trapez je štiristranski mnogokotnik ali štirikotnik, za katerega je značilno, da ima en par vzporednih stranic, imenovanih osnove, medtem ko drugi dve strani, znani kot kraki, nista vzporedni. Trapez, ki je pogost v vsakdanjih predmetih, kot so mize, je znan po svojih geometrijskih lastnostih: ima višino, ki je pravokotna razdalja med osnovama, in mediano, ki povezuje razpolovni točki nevzporednih stranic in je vzporedna z osnovami.
Ploščino trapeza izračunamo tako, da povprečje dolžin osnov pomnožimo z višino, njegov obseg pa je vsota vseh njegovih stranic. Z različnimi klasifikacijami, kot so skalni, enakokraki in pravi trapezi, od katerih ima vsak edinstvene lastnosti stranice in kota, so trapezi temeljni tako v praktičnih aplikacijah kot v geometrijski teoriji.
Pogosta vprašanja o trapezu pri matematiki
Kaj je oblika trapeza?
Trapez je štirikotnik, v katerem je par premic vedno vzporeden. Po obliki spominja na mizo. Njegovo ime je vzeto iz grške besede trapeze, kar pomeni miza.
Koliko vrst trapeza?
Obstajata dve vrsti trapeza,
- Navadni trapez: V katerem je drugi par črt enak.
- Nepravilni trapez: Pri kateri drugi par črt ni enak.
Koliko vzporednih stranic ima trapez?
Vemo, da je trapez štirikotnik z enim parom vzporednih stranic. Tako ima trapez par vzporednih črt (stranic).
Ali lahko trapez štejemo za štirikotnik?
A ima štiri stranice, štiri oglišča in štiri kote. Zato ga lahko štejemo za štirikotnik, vsota vseh štirih notranjih kotov trapeza je 360 stopinj.
Ali lahko kvadrat imenujemo trapez?
Trapez je štirikotnik s samo enim parom vzporednih stranic, drugi dve strani pa sta nevzporedni. Toda v primeru kvadrata ima dva para vzporednih stranic, zato ga ni mogoče šteti za trapez.
Ali so diagonale trapeza vedno enake?
Diagonale trapeza morda niso enake. V primeru pravilnega mnogokotnika sta diagonali enaki, vendar to ne drži v primeru nepravilnega mnogokotnika.
Kakšne so lastnosti trapeza?
5 lastnosti trapeza so:
- V trapezu sta osnovici med seboj vzporedni.
- Trapez ima dodatne sosednje kote.
- Le en par nasprotnih stranic je vzporeden.
- Vsota vseh notranjih kotov v trapezu je vedno 360°.
- Premica, ki povezuje razpolovišče nevzporednih stranic, je vedno vzporedna z osnovami.
