Topološko razvrščanje za Usmerjeni aciklični graf (DAG) je linearna ureditev oglišč, tako da za vsak usmerjen rob u-v velja oglišče v prihaja prej v pri naročanju.
Opomba: Topološko razvrščanje za graf ni mogoče, če graf ni a DAN .
primer:
Priporočena praksaRešitev, ki temelji na DFS, za iskanje topološkega razvrščanja že razpravljali.Vnos: Graf:
Primer
Izhod: 5 4 2 3 1 0
Pojasnilo: Prvo oglišče pri topološkem razvrščanju je vedno oglišče z notranjo stopnjo 0 (oglišče brez vhodnih robov). Topološko razvrščanje naslednjega grafa je 5 4 2 3 1 0. Za graf je lahko več kot eno topološko razvrščanje. Drugo topološko razvrščanje naslednjega grafa je 4 5 2 3 1 0.
kaj je sklad java
Topološki red morda ni edinstven:
Topološko razvrščanje je problem odvisnosti, pri katerem je dokončanje ene naloge odvisno od dokončanja več drugih nalog, katerih vrstni red se lahko spreminja. Razumejmo ta koncept na primeru:
Recimo, da je naša naloga priti do naše šole in da bi prispeli tja, se moramo najprej obleči. Odvisnosti od nošenja oblačil so prikazane v spodnjem grafu odvisnosti. Na primer, ne morete nositi čevljev, preden nosite nogavice.
Iz zgornje slike bi že ugotovili, da obstaja več načinov, kako se obleči, spodnja slika prikazuje nekatere od teh načinov.
Lahko našteješ vso možno topološko urejenost oblačenja za zgornji graf odvisnosti?
Algoritem za topološko razvrščanje z uporabo DFS:
Tukaj je algoritem po korakih za topološko razvrščanje z uporabo iskanja najprej v globino (DFS):
- Ustvari graf z n oglišča in m - usmerjeni robovi.
- Inicializirajte sklad in obiskano matriko velikosti n .
- Za vsako neobiskano točko v grafu naredite naslednje:
- Pokličite funkcijo DFS z vozliščem kot parametrom.
- V funkciji DFS označite vozlišče kot obiskano in rekurzivno pokličite funkcijo DFS za vse neobiskane sosede vozlišča.
- Ko so vsi sosedi obiskani, potisnite točko na sklad.
- Konec koncev so bile točke obiskane, izločite elemente iz sklada in jih dodajte na izhodni seznam, dokler sklad ni prazen.
- Nastali seznam je topološko razvrščen vrstni red grafa.
Ilustracija Algoritem topološkega razvrščanja:
Spodnja slika je ilustracija zgornjega pristopa:

Celoten potek dela topološkega razvrščanja
Korak 1:
- DFS zaženemo iz vozlišča 0, ker nima nič dohodnih vozlišč
- Vozlišče 0 potisnemo v sklad in se premaknemo na naslednje vozlišče z minimalnim številom sosednjih vozlišč, tj. vozlišče 1.
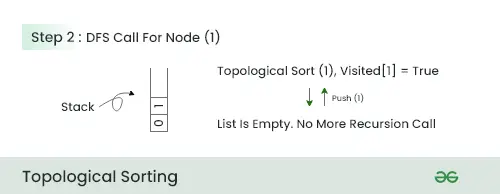
2. korak:
- Ker v tem koraku ni sosednjega vozlišča, potisnite vozlišče 1 v sklad in se premaknite na naslednje vozlišče.
3. korak:
- V tem koraku smo izbrali vozlišče 2, ker ima najmanjše število sosednjih vozlišč po 0 in 1.
- Pokličemo DFS za vozlišče 2 in potisnemo vsa vozlišča, ki pridejo v prehod iz vozlišča 2, v obratnem vrstnem redu.
- Torej pritisnite 3 in nato pritisnite 2.
uri proti url4. korak:
- Zdaj kličemo DFS za vozlišče 4
- Ker sta 0 in 1 že prisotna v skladu, zato samo potisnemo vozlišče 4 v sklad in se vrnemo.
5. korak:
- V tem koraku, ker so vsa sosednja vozlišča od 5 že v skladu, potisnemo vozlišče 5 v sklad in se vrnemo.
6. korak: To je zadnji korak topološkega razvrščanja, pri katerem odstranimo vse elemente iz sklada in jih natisnemo v tem vrstnem redu.
Spodaj je izvedba zgornjega pristopa:
C++ #include using namespace std; // Function to perform DFS and topological sorting void topologicalSortUtil(int v, vector>& adj, vektor & obiskal, sklad & Stack) { // Označi trenutno vozlišče kot obiskano visited[v] = true; // Ponavlja se za vse sosednje točke for (int i : adj[v]) { if (!visited[i]) topologicalSortUtil(i, adj, visited, Stack); } // Potisni trenutno točko v sklad, ki shrani rezultat Stack.push(v); } // Funkcija za izvedbo topološkega razvrščanja void topologicalSort(vector>& adj, int V) { sklad Stack; // Sklad za shranjevanje vektorja rezultata obiskano (V, napačno); // Pokliči rekurzivno pomožno funkcijo za shranjevanje // Topološko razvrščanje, začenši od vseh tock enega po // enega za (int i = 0; i< V; i++) { if (!visited[i]) topologicalSortUtil(i, adj, visited, Stack); } // Print contents of stack while (!Stack.empty()) { cout << Stack.top() << ' '; Stack.pop(); } } int main() { // Number of nodes int V = 4; // Edges vector> robovi = { { 0, 1 }, { 1, 2 }, { 3, 1 }, { 3, 2 } }; // Graf, predstavljen kot vektor seznama sosednosti> adj(V); za (auto i : robovi) { adj[i[0]].push_back(i[1]); } cout<< 'Topological sorting of the graph: '; topologicalSort(adj, V); return 0; }>
Java import java.util.*; public class TopologicalSort { // Function to perform DFS and topological sorting static void topologicalSortUtil(int v, List> adj, boolean [] obiskano, Stack stack) { // Označi trenutno vozlišče kot obiskano visited[v] = true; // Ponavlja se za vse sosednje točke for (int i : adj.get(v)) { if (!visited[i]) topologicalSortUtil(i, adj, visited, stack); } // Potisni trenutno točko v sklad, ki shrani // rezultat stack.push(v); } // Funkcija za izvedbo topološkega razvrščanja static void topologicalSort(List> adj, int V) { // Sklad za shranjevanje rezultata Sklad stack = new Stack(); logična vrednost [] obiskano = nova logična vrednost [V]; // Pokliči rekurzivno pomočno funkcijo za shranjevanje // Topološko razvrščanje, začenši od vseh tock enega // enega za (int i = 0; i< V; i++) { if (!visited[i]) topologicalSortUtil(i, adj, visited, stack); } // Print contents of stack System.out.print( 'Topological sorting of the graph: '); while (!stack.empty()) { System.out.print(stack.pop() + ' '); } } // Driver code public static void main(String[] args) { // Number of nodes int V = 4; // Edges List> robovi = nov ArrayList(); edges.add(Arrays.asList(0, 1)); edges.add(Arrays.asList(1, 2)); edges.add(Arrays.asList(3, 1)); edges.add(Arrays.asList(3, 2)); // Graf, predstavljen kot seznam sosednosti List> adj = nov ArrayList(V); za (int i = 0; i< V; i++) { adj.add(new ArrayList()); } for (List i : robovi) { adj.get(i.get(0)).add(i.get(1)); } topologicalSort(adj, V); } }>
Python3 def topologicalSortUtil(v, adj, visited, stack): # Mark the current node as visited visited[v] = True # Recur for all adjacent vertices for i in adj[v]: if not visited[i]: topologicalSortUtil(i, adj, visited, stack) # Push current vertex to stack which stores the result stack.append(v) # Function to perform Topological Sort def topologicalSort(adj, V): # Stack to store the result stack = [] visited = [False] * V # Call the recursive helper function to store # Topological Sort starting from all vertices one by # one for i in range(V): if not visited[i]: topologicalSortUtil(i, adj, visited, stack) # Print contents of stack print('Topological sorting of the graph:', end=' ') while stack: print(stack.pop(), end=' ') # Driver code if __name__ == '__main__': # Number of nodes V = 4 # Edges edges = [[0, 1], [1, 2], [3, 1], [3, 2]] # Graph represented as an adjacency list adj = [[] for _ in range(V)] for i in edges: adj[i[0]].append(i[1]) topologicalSort(adj, V)> C# using System; using System.Collections.Generic; class Program { // Function to perform DFS and topological sorting static void TopologicalSortUtil(int v, List> adj, bool[] obiskano, Stack stack) { // Označi trenutno vozlišče kot obiskano visited[v] = true; // Ponavlja se za vsa sosednja vozlišča foreach(int i in adj[v]) { if (!visited[i]) TopologicalSortUtil(i, adj, visited, stack); } // Potisnite trenutno točko v sklad, ki shrani // rezultatni sklad.Push(v); } // Funkcija za izvedbo topološkega razvrščanja static void TopologicalSort(List> adj, int V) { // Sklad za shranjevanje rezultata Sklad sklad = nov sklad (); bool[] obiskan = nov bool[V]; // Pokliči rekurzivno pomožno funkcijo za shranjevanje // Topološko razvrščanje, začenši z vsemi točkami eno za drugo za (int i = 0; i< V; i++) { if (!visited[i]) TopologicalSortUtil(i, adj, visited, stack); } // Print contents of stack Console.Write('Topological sorting of the graph: '); while (stack.Count>0) { Console.Write(stack.Pop() + ' '); } } // Koda gonilnika static void Main(string[] args) { // Število vozlišč int V = 4; // Seznam robov> robovi = nov seznam>{ nov seznam { 0, 1 }, nov seznam { 1, 2 }, nov seznam { 3, 1 }, nov seznam { 3, 2 } }; // Graf, predstavljen kot seznam sosednosti List> adj = nov seznam>(); za (int i = 0; i< V; i++) { adj.Add(new List ()); } foreach(Seznam i v robovih) { adj[i[0]].Add(i[1]); } Topološka vrsta (adj, V); } }>
Javascript // Function to perform DFS and topological sorting function topologicalSortUtil(v, adj, visited, stack) { // Mark the current node as visited visited[v] = true; // Recur for all adjacent vertices for (let i of adj[v]) { if (!visited[i]) topologicalSortUtil(i, adj, visited, stack); } // Push current vertex to stack which stores the result stack.push(v); } // Function to perform Topological Sort function topologicalSort(adj, V) { // Stack to store the result let stack = []; let visited = new Array(V).fill(false); // Call the recursive helper function to store // Topological Sort starting from all vertices one by // one for (let i = 0; i < V; i++) { if (!visited[i]) topologicalSortUtil(i, adj, visited, stack); } // Print contents of stack console.log('Topological sorting of the graph: '); while (stack.length>0) { console.log(stack.pop() + ' '); } } // Koda gonilnika (() => { // Število vozlišč const V = 4; // Robovi const robovi = [[0, 1], [1, 2], [3, 1], [3, 2]]; // Graf, predstavljen kot seznam sosednosti const adj = Array.from({ length: V }, () => []); for (let i of edges) { adj[i[0]].push (i[1]); topologicalSort(adj, V);> Izhod
Topological sorting of the graph: 3 0 1 2>
Časovna zapletenost: O(V+E). Zgornji algoritem je preprosto DFS z dodatnim skladom. Časovna zapletenost je torej enaka DFS
Pomožni prostor: O(V). Za sklad je potreben dodaten prostor
Topološko razvrščanje z BFS:
C++ #include #include #include using namespace std; // Class to represent a graph class Graph { int V; // No. of vertices list * adj; // Kazalec na matriko, ki vsebuje // sezname sosednosti public: Graph(int V); // Konstruktor void addEdge(int v, int w); // Funkcija za dodajanje roba grafu void topologicalSort(); // natisne topološko sortiranje // celotnega grafa }; Graf::Graf(int V) { this->V = V; adj = nov seznam [V]; } void Graph::addEdge(int v, int w) { adj[v].push_back(w); // Dodaj w na v-jev seznam. } // Funkcija za izvedbo topološkega razvrščanja void Graph::topologicalSort() { // Ustvari vektor za shranjevanje vektorja v stopinjah vseh vozlišč v_stopnji (V, 0); // Preleti sezname sosednosti, da zapolni in_degree // tock za (int v = 0; v< V; ++v) { for (auto const& w : adj[v]) in_degree[w]++; } // Create a queue and enqueue all vertices with // in-degree 0 queue q; za (int i = 0; i< V; ++i) { if (in_degree[i] == 0) q.push(i); } // Initialize count of visited vertices int count = 0; // Create a vector to store topological order vector top_order; // Eno po eno odstrani točko iz čakalne vrste in postavi v čakalno vrsto // sosednjo točko, če stopnja sosednjega postane 0, medtem ko (!q.empty()) { // Ekstrahiraj sprednjo stran čakalne vrste (ali izvedi odstranitev iz čakalne vrste) // in jo dodaj v topološki red int u = q.front(); q.pop(); top_order.push_back(u); // Iteracija skozi vsa sosednja vozlišča // vozlišča u, ki je izločeno iz čakalne vrste, in zmanjšanje njihove stopnje // za 1 seznam ::iterator itr; for (itr = adj[u].begin(); itr != adj[u].end(); ++itr) // Če in-degree postane nič, ga dodajte v čakalno vrsto if (--in_degree[*itr) ] == 0) q.push(*itr); štetje++; } // Preverite, ali je prišlo do cikla if (count != V) { cout<< 'Graph contains cycle
'; return; } // Print topological order for (int i : top_order) cout << i << ' '; } // Driver code int main() { // Create a graph given in the above diagram Graph g(6); g.addEdge(5, 2); g.addEdge(5, 0); g.addEdge(4, 0); g.addEdge(4, 1); g.addEdge(2, 3); g.addEdge(3, 1); cout << 'Following is a Topological Sort of the given ' 'graph
'; g.topologicalSort(); return 0; }> Java import java.util.ArrayList; import java.util.LinkedList; import java.util.Queue; // Class to represent a graph class Graph { private int V; // No. of vertices private ArrayList [] adj; // Seznam sosednosti // predstavitev // grafa // Konstruktor Graph(int V) { this.V = V; adj = nov ArrayList[V]; za (int i = 0; i< V; ++i) adj[i] = new ArrayList(); } // Function to add an edge to the graph void addEdge(int v, int w) { adj[v].add(w); // Add w to v’s list. } // Function to perform Topological Sort void topologicalSort() { // Create an array to store in-degree of all // vertices int[] inDegree = new int[V]; // Calculate in-degree of each vertex for (int v = 0; v < V; ++v) { for (int w : adj[v]) { inDegree[w]++; } } // Create a queue and enqueue all vertices with // in-degree 0 Queue q = nov LinkedList(); za (int i = 0; i< V; ++i) { if (inDegree[i] == 0) q.add(i); } // Initialize count of visited vertices int count = 0; // Create an ArrayList to store topological order ArrayList topOrder = nov ArrayList(); // Eno za drugim odstrani točke iz čakalne vrste in // postavi sosednje točke v čakalno vrsto, če na stopnji // sosednje postane 0 while (!q.isEmpty()) { // Ekstrahiraj sprednjo stran čakalne vrste in jo dodaj v // topološki red int u = q.poll(); topOrder.add(u); štetje++; // Ponovi skozi vsa sosednja vozlišča // vozlišča u, ki je izločeno iz čakalne vrste, in zmanjšaj njihovo stopnjo // za 1 za (int w : adj[u]) { // Če stopnja postane nič, jo dodaj v // čakalno vrsto if (--inDegree[w] == 0) q.add(w); } } // Preveri, ali je bil cikel if (count != V) { System.out.println('Graf vsebuje cikel'); vrnitev; } // Natisni topološki vrstni red za (int i : topOrder) System.out.print(i + ' '); } } // Koda gonilnika public class Main { public static void main(String[] args) { // Ustvari graf, podan v zgornjem diagramu Graph g = new Graph(6); g.addEdge(5, 2); g.addEdge(5, 0); g.addEdge(4, 0); g.addEdge(4, 1); g.addEdge(2, 3); g.addEdge(3, 1); System.out.println( 'Sledi topološka vrsta danega grafa'); g.topologicalSort(); } }> Python3 from collections import defaultdict class Graph: def __init__(self, vertices): # Number of vertices self.V = vertices # Dictionary to store adjacency lists self.adj = defaultdict(list) def addEdge(self, u, v): # Function to add an edge to the graph self.adj[u].append(v) def topologicalSort(self): # Function to perform Topological Sort # Create a list to store in-degree of all vertices in_degree = [0] * self.V # Traverse adjacency lists to fill in_degree of vertices for i in range(self.V): for j in self.adj[i]: in_degree[j] += 1 # Create a queue and enqueue all vertices with in-degree 0 q = [] for i in range(self.V): if in_degree[i] == 0: q.append(i) # Initialize count of visited vertices count = 0 # Create a list to store topological order top_order = [] # One by one dequeue vertices from queue and enqueue # adjacent vertices if in-degree of adjacent becomes 0 while q: # Extract front of queue (or perform dequeue) # and add it to topological order u = q.pop(0) top_order.append(u) # Iterate through all its neighbouring nodes # of dequeued node u and decrease their in-degree # by 1 for node in self.adj[u]: # If in-degree becomes zero, add it to queue in_degree[node] -= 1 if in_degree[node] == 0: q.append(node) count += 1 # Check if there was a cycle if count != self.V: print('Graph contains cycle') return # Print topological order print('Topological Sort:', top_order) # Driver code if __name__ == '__main__': # Create a graph given in the above diagram g = Graph(6) g.addEdge(5, 2) g.addEdge(5, 0) g.addEdge(4, 0) g.addEdge(4, 1) g.addEdge(2, 3) g.addEdge(3, 1) print('Following is a Topological Sort of the given graph') g.topologicalSort()> JavaScript // Class to represent a graph class Graph { constructor(V) { this.V = V; // No. of vertices this.adj = new Array(V); // Array containing adjacency lists for (let i = 0; i < V; i++) { this.adj[i] = []; } } // Function to add an edge to the graph addEdge(v, w) { this.adj[v].push(w); // Add w to v’s list. } // Function to perform Topological Sort topologicalSort() { // Create a array to store in-degree of all vertices let inDegree = new Array(this.V).fill(0); // Traverse adjacency lists to fill inDegree of vertices for (let v = 0; v < this.V; v++) { for (let w of this.adj[v]) { inDegree[w]++; } } // Create a queue and enqueue all vertices with in-degree 0 let queue = []; for (let i = 0; i < this.V; i++) { if (inDegree[i] === 0) { queue.push(i); } } // Initialize count of visited vertices let count = 0; // Create an array to store topological order let topOrder = []; // One by one dequeue vertices from queue and enqueue // adjacent vertices if in-degree of adjacent becomes 0 while (queue.length !== 0) { // Extract front of queue and add it to topological order let u = queue.shift(); topOrder.push(u); // Iterate through all its neighboring nodes // of dequeued node u and decrease their in-degree by 1 for (let w of this.adj[u]) { // If in-degree becomes zero, add it to queue if (--inDegree[w] === 0) { queue.push(w); } } count++; } // Check if there was a cycle if (count !== this.V) { console.log('Graph contains cycle'); return; } // Print topological order console.log('Topological Sort of the given graph:'); console.log(topOrder.join(' ')); } } // Driver code // Create a graph given in the above diagram let g = new Graph(6); g.addEdge(5, 2); g.addEdge(5, 0); g.addEdge(4, 0); g.addEdge(4, 1); g.addEdge(2, 3); g.addEdge(3, 1); console.log('Following is a Topological Sort of the given graph:'); g.topologicalSort(); //This code is contributed by Utkarsh> Izhod
Following is a Topological Sort of the given graph 4 5 2 0 3 1>
Časovna zapletenost:
Časovna zahtevnost izdelave grafa je O(V + E), kjer je V število oglišč in E število robov.
Časovna zahtevnost za izvedbo topološkega razvrščanja z uporabo BFS je tudi O(V + E), kjer je V število vozlišč in E število robov. To je zato, ker se vsako vozlišče in vsak rob obišče enkrat med prehodom BFS.
Kompleksnost prostora:
Prostorska kompleksnost za shranjevanje grafa z uporabo seznama sosednosti je O(V + E), kjer je V število vozlišč in E število robov.
Dodaten prostor se uporablja za shranjevanje in-stopenj oglišč, kar zahteva O(V) prostora.
Za prehod BFS se uporablja čakalna vrsta, ki lahko vsebuje največ V vozlišč. Tako je kompleksnost prostora za čakalno vrsto O(V).
ukaz sed
Na splošno je prostorska kompleksnost algoritma O(V + E) zaradi shranjevanja grafa, matrike v stopinjah in čakalne vrste.
Če povzamemo, je časovna zahtevnost podane izvedbe O(V + E), prostorska pa prav tako O(V + E).
Opomba: Tukaj lahko namesto sklada uporabimo tudi polje. Če je uporabljena matrika, natisnite elemente v obratnem vrstnem redu, da dobite topološko razvrščanje.
Prednosti topološkega razvrščanja:
- Pomaga pri načrtovanju nalog ali dogodkov na podlagi odvisnosti.
- Zazna cikle v usmerjenem grafu.
- Učinkovito za reševanje problemov z omejitvami prednosti.
Slabosti topološkega razvrščanja:
- Uporabno samo za usmerjene aciklične grafe (DAG), ni primerno za ciklične grafe.
- Morda ni edinstven, obstaja lahko več veljavnih topoloških vrstnih redov.
- Neučinkovito za velike grafe s številnimi vozlišči in robovi.
Aplikacije topološkega razvrščanja:
- Načrtovanje nalog in vodenje projektov.
- Reševanje odvisnosti v sistemih za upravljanje paketov.
- Določanje vrstnega reda prevajanja v sistemih za gradnjo programske opreme.
- Zaznavanje zastoja v operacijskih sistemih.
- Razpored tečajev na univerzah.
Povezani članki:
- Kahnov algoritem za topološko razvrščanje
- Vse topološke vrste usmerjenega acikličnega grafa