Trigonometrija je pomembna veja matematike, ki se ukvarja z razmerjem med koti in dolžinami stranic pravokotnega trikotnika. Šest trigonometričnih razmerij ali funkcij je sinus, kosinus, tangens, kosekans in sekans, trigonometrično razmerje pa je razmerje med stranicami pravokotnega trikotnika. Funkcije sinusa, kosinusa in tangensa so tri pomembne trigonometrične funkcije, saj so ostale tri, tj. funkcije kosekans, sekans in kotangens, recipročne funkcije funkcij sinusa, kosinusa in tangensa.
- sin θ = Nasprotna stranica/hipotenuza
- cos θ = sosednja stran/hipotenuza
- tan θ = nasprotna stran/sosednja stran
- cosec θ = hipotenuza/nasprotna stran
- sec θ = hipotenuza/sosednja stran
- posteljica θ = sosednja stran/nasprotna stran
Tangentna funkcija je ena od 6 trigonometričnih funkcij, ki se uporabljajo v trigonometrične formule .
Kazalo
Tangentna formula
Tangens kota v pravokotnem trikotniku je razmerje med dolžino nasprotne stranice in dolžino sosednje strani danemu kotu. Funkcijo tangente zapišemo kot tan. Vzemimo pravokotni trikotnik XYZ in eden od njegovih ostrih kotov je θ. Nasprotna stranica je stran, ki je nasprotna kotu θ, sosednja stran pa stran, ki meji na kot θ.
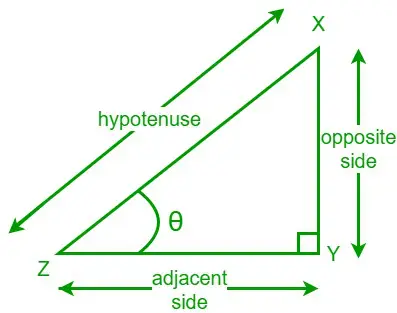
Formula tangente za dani kot θ je,
tan θ = nasprotna stran/sosednja stran
Nekaj osnovnih formul tangente
Tangentna funkcija v kvadrantih
Funkcija tangente je pozitivna v prvem in tretjem kvadrantu ter negativna v drugem in četrtem kvadrantu.
- tan (2π + θ) = tan θ (1stkvadrant)
- tan (π – θ) = – tan θ (2ndkvadrant)
- tan (π + θ) = tan θ (3rdkvadrant)
- tan (2π – θ) = – tan θ (4thkvadrant)
Tangentna funkcija kot negativna funkcija
Funkcija tangente je negativna funkcija, saj je tangens negativnega kota negativen kot tangente pozitivnega kota.
tan (-θ) = – tan θ
Tangentna funkcija v smislu sinusne in kosinusne funkcije
Tangentno funkcijo v smislu sinusne in kosinusne funkcije lahko zapišemo kot
tan θ = sin θ/cos θ
Vemo, da je tan θ = nasprotna stran/sosednja stran
Zdaj delite števec in imenovalec s hipotenuzo
tan θ = (nasprotna stran/hipotenuza)/(sosednja stranica/hipotenuza)
Vemo, da je sin θ = nasprotna stran/hipotenuza
cos θ = sosednja stranica/hipotenuza
Zato je tan θ = sin θ/cos θ
Tangentna funkcija v smislu sinusne funkcije
Funkcijo tangente v smislu sinusne funkcije lahko zapišemo kot
tan θ = sin θ/(√1 – sin 2 jaz)
Vemo, da
tan θ = sin θ/cos θ
kako prenesti glasbo
Iz pitagorejskih identitet imamo,
brez2θ + cos2θ = 1
cos2θ = 1 – sin2jaz
cos θ = √(1 – sin2jaz)
Zato je tan θ = sin θ/(√1 – sin2jaz)
Tangentna funkcija v smislu kosinusne funkcije
Tangentno funkcijo v smislu kosinusne funkcije lahko zapišemo kot
tan θ = (√1 -cos 2 i)/cos i
Vemo, da
tan θ = sin θ/cos θ
Iz pitagorejskih identitet imamo,
brez2θ + cos2θ = 1
brez2θ = 1 – cos2jaz
sin θ = √(1 – cos2jaz)
Zato je tan θ = (√1 – cos2i)/cos i
Funkcija tangensa v smislu funkcije kotangens
Funkcijo tangente v smislu funkcije kotangensa lahko zapišemo kot
tan θ = 1/otroška posteljica θ
oz
tan θ = posteljica (90° – θ) (ali) posteljica (π/2 – θ)
Tangentna funkcija v terminih kosekantne funkcije
Funkcijo tangente v smislu funkcije kosekansa lahko zapišemo kot
tan θ = 1/√(cosec 2 i – 1)
Iz pitagorejskih identitet imamo,
cosec2θ – posteljica2θ = 1
otroška posteljica2θ = cosec2i – 1
cot θ = √(cosec2i – 1)
Vemo, da
tan θ = 1/otroška posteljica θ
Zato je tan θ = 1/√(cosec2i – 1)
Tangentna funkcija v terminih sekantne funkcije
Funkcijo tangente v smislu funkcije sekante lahko zapišemo kot
tan θ = √sek 2 i – 1
Iz pitagorejskih identitet imamo,
sek2θ – torej2θ = 1
tan θ = sek2i – 1
Zato je tan θ = √(sek2i – 1)
Funkcija tangente v smislu dvojnega kota
Tangentna funkcija za dvojni kot je,
tan 2θ = (2 tan θ)/(1 – tan 2 jaz)
Tangentna funkcija v smislu trojnega kota
Tangentna funkcija za trojni kot je,
tan 3θ = (3 tan θ – tan 3 θ) / (1 – 3 tan 2 jaz)
Funkcija tangente v terminih polovičnega kota
Funkcija tangente za pol-kota je,
tan (θ/2) = ± √[ (1 – cos θ) / (1 + cos θ) ]
tan (θ/2) = (1 – cos θ) / (sin θ)
Funkcija tangente v smislu seštevanja in odštevanja dveh kotov
Formule vsote in razlike za tangentno funkcijo so:
tan (A + B) = (tan A + tan B)/(1 – tan A tan B)
tan (A – B) = (tan A – tan B)/(1 + tan A tan B)
Tabela trigonometričnega razmerja
| Kot (v stopinjah) | Kot (v radianih) | greh i | cos θ | tan θ = sin θ/cos θ | cosec θ | sekunda θ | posteljica i |
|---|---|---|---|---|---|---|---|
| 0° | 0 | 0 | 1 | 0/1 = 0 | Nedoločeno | 1 | Nedoločeno |
| 30° | str/6 | 1/2 | √3/2 | (1/2)/(√3/2) = 1/√3 | 2 | 23 | √3 |
| 45° | str/4 | 1/√2 | 1/√2 | (1/√2)/(1/√2) = 1 | √2 | √2 | 1 |
| 60° | p/3 | √3/2 | 1/2 | (√3/2)/(1/2) = √3 centriranje slik v css | 23 | 2 | 1/√3 |
| 90° | p/2 | 1 | 0 | 1/0 = nedefinirano | 1 | Nedoločeno | 0 |
| 120° | 2p/3 | √3/2 | -1/2 | (√3/2)/(-1/2) = -√3 | 23 | -2 | -1/√3 |
| 150° | 5p/6 | 1/2 | -(√3/2) | (1/2)/(-√3/2) = -1/√3 | 2 | -(23) | -√3 |
| 180° | Pi | 0 | -1 | 0/(-1) = 0 | Nedoločeno | -1 | Nedoločeno |
Rešen primer tangentnih formul
Primer 1: Poiščite vrednost tan θ, če je sin θ = 2/5 in je θ kot prvega kvadranta.
rešitev:
podano,
- sin θ = 2/5
Iz pitagorejskih identitet, ki jih imamo,
brez2θ + cos2θ = 1
cos2θ = 1 – sin2θ = 1 – (2/5)2
cos2θ = 1 – (4/5) = 21/25
cos θ = ±√21/5
Ker je θ kot prvega kvadranta, je cos θ pozitiven.
cos θ = √21/5
Vemo, da
tan θ = sin θ/cos θ
= (2/5)/(√21/5) = 2/√21
tan θ = 2√21 /21
Torej je vrednost tan θ, ko je sin θ = 2/5 in je θ v prvem kvadrantu (2√21) /(21)
Primer 2: Poiščite vrednost tan x, če je sec x = 13/12 in je x kot četrtega kvadranta.
rešitev:
dodajte niz java
Podano, sek x = 13/12
Iz pitagorejskih identitet imamo,
sek2x – torej2x = 1
torej2x = sekunda2x – 1= (13/12)2- 1
torej2x = (169/144) – 1 = 25/144
tan x = ± 5/12
Ker je x kot četrtega kvadranta, je tan x negativen.
tan x = – 5/12
torej tan x = – 5/12
Primer 3: Če je tan X = 2/3 in tan Y = 1/2, kakšna je potem vrednost tan (X + Y)?
rešitev:
podano,
tan X = 2/3 in tan Y = 1/2
Vemo, da
tan (X + Y) = (tan X + tan Y)/(1 – tan X tan Y)
tan (X + Y) = [(2/3) + (1/2)]/[1 – (2/3)×(1/2)]
= (7/6)/(2/3) = 7/4
torej tan (X + Y) = 7/4
4. primer: Izračunajte tangentno funkcijo, če sta sosednji in nasprotni stranici pravokotnega trikotnika 4 cm oziroma 7 cm.
rešitev:
podano,
Sosednja stran = 4 cm
Nasprotna stran = 7 cm
Vemo, da
tan θ = nasprotna stran/sosednja stran
tan θ = 7/4 = 1,75
torej tan θ = 1,75
Primer 5: Moški gleda stolp z uro pod kotom 60° glede na vrh stolpa, katerega višina je 100 m. Kolikšna je razdalja med človekom in vznožjem stolpa?
rešitev:
podano,
Višina stolpa = 100 m in θ = 60°
Naj bo razdalja med človekom in vznožjem stolpa = d
Imamo,
tan θ = nasprotna stran/sosednja stran
tan 60° = 100/d
√3 = 100/d [Ker je torej 60° = √3]
d = 100/√3
Zato je razdalja med človekom in vznožjem stolpa enaka 100/√3
Primer 6: Poiščite vrednost tan θ, če je sin θ = 7/25 in sec θ = 25/24.
rešitev:
podano,
sin θ = 7/25
sec θ = 25/24
Vemo, da
sec θ = 1/cos θ
25/24 = 1/cos θ cos θ = 24/25
Imamo,
tan θ = sin θ/cos θ
= (7/25)/(24/25)
= 7/24
torej tan θ = 7/24
Primer 7: Poiščite vrednost tan θ, če je cosec θ = 5/3 in je θ kot prvega kvadranta.
rešitev:
Glede na cosec θ = 5/3
Iz pitagorejskih identitet imamo,
string.format javacosec2θ – posteljica2θ = 1
otroška posteljica2θ = cosec2i – 1
posteljica θ = (5/3)2– 1 = (25/9) – 1 = 16/9
posteljica θ = ±√16/9 = ± 4/3
Ker je θ kot prvega kvadranta, sta funkciji kotangens in tangens pozitivni.
posteljica θ = 4/3
Vemo, da
posteljica θ = 1/tan θ
4/3 = 1/tanθ
tan θ = 3/4
torej tan θ = 3/4
Primer 8: Poiščite tan 3θ, če je sin θ = 3/7 in je θ kot prvega kvadranta.
rešitev:
Glede na sin θ = 12/13
Iz pitagorejskih identitet, ki jih imamo,
brez2θ + cos2θ = 1
cos2θ = 1 – sin2θ = 1 – (12/13)2
cos2 θ = 1 – (144/169) = 25/169
cos θ = ±√25/169 = ±5/13
Ker je θ kot prvega kvadranta, je cos θ pozitiven.
cos θ = 5/13
Vemo, da
tan θ = sin θ/cos θ
= (12/25)/(5/13) = 12/5
Zato je tan θ = 12/5
Zdaj vemo, da
tan 3θ = (3 tan θ – tan3θ) / (1 – 3 tan2θ)
tan 3θ = 3 × (12/5)

