Površina prizme: V matematiki je prizma bistveni član družine poliedrov in je opredeljena kot tridimenzionalna oblika z dvema enakima mnogokotnikoma, obrnjenima drug proti drugemu, ki sta stransko povezana s pravokotnimi ali paralelogramskimi ploskvami. Enaki mnogokotniki so lahko trikotniki, kvadrati, pravokotniki, peterokotniki ali kateri koli drug n-stranski mnogokotnik in se imenujejo osnove prizme. Druge ploskve prizme so paralelogrami ali pravokotniki.

V tem članku bomo razpravljali različne vrste prizem in formula za površino prizme s primeri in vadbenimi nalogami.

Kazalo

• Kakšna je površina prizme?
• Različne vrste prizm
• Trikotna prizma
• Pravokotna prizma
• Kvadratna prizma
• Peterokotna prizma
• Šesterokotna prizma
• Formula za površino prizme
• Površina prizme Rešeni primeri
• Vadbene naloge o površini prizme

Kakšna je površina prizme?

Površina prizme se imenuje skupna površina, ki jo obdajajo vse njene ploskve. Za določitev površine prizme moramo izračunati površine vsake njene ploskve in nato sešteti dobljene površine. Prizma ima dve vrsti površin, in sicer stransko površino in celotno površino. Območje, ki ga zavzemajo ploskve prizme, razen dveh vzporednih ploskev (osnove prizme), se imenuje njena stranska površina.

Bočna površina prizme = [Osnovni obseg × višina] kvadratnih enot

Zdaj je skupna površina prizme vsota ploščin njenih dveh baz in njene stranske površine.

Splošna formula za izračun celotne površine katere koli vrste desne prizme je:

Skupna površina prizme = [2 (osnovna površina) + (osnovni obseg × višina)] kvadratnih enot

Različne vrste prizm

Obstajajo različne vrste prizem glede na obliko baze prizme, kot npr

• Trikotne prizme,
• kvadratne prizme,
• pravokotne prizme,
• peterokotne prizme,
• šesterokotne prizme,
• Osmerokotne prizme.

Trikotna prizma

Prizma s trikotno osnovo se imenuje trikotna prizma. Trikotna prizma je sestavljena iz treh nagnjenih pravokotnih ploskev in dveh vzporednih trikotnih baz. Naj bo H višina trikotne prizme; a, b in c so dolžine stranic, h pa višina trikotnih osnov.

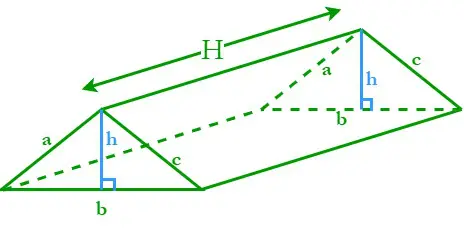
Obseg trikotne osnove (P) = vsota njegovih treh strani = a + b + c

Ploščina trikotne osnove (A) = ½ × osnova × višina = ½ bh

Vemo, da je splošna formula za stranska ploskev desne prizme je L. S. A. = PH, kjer je P osnovni obseg, A pa osnovna ploskev.

Z zamenjavo vseh vrednosti v splošni formuli dobimo ,

Bočna površina trikotne prizme = (a + b +c)H kvadratnih enot

kje,

a, b, c so stranice trikotne osnove

H je višina trikotne prizme

Vemo, da je splošna formula za skupno površino desne prizme T. S. A. = PH+2A, kjer je P osnovni obseg, A osnovna ploščina in H višina prizme.

Z zamenjavo vseh vrednosti v splošni formuli dobimo

Skupna površina trikotne prizme = (a + b + c)H + 2 × (½ bh)

Skupna površina trikotne prizme = (a + b + c)H + bh kvadratnih enot

kje,

a, b, c so stranice trikotne osnove

H je višina trikotne prizme

h je višina trikotnika

Pravokotna prizma

Prizma s pravokotno osnovo se imenuje pravokotna prizma. Pravokotna prizma je sestavljena iz štirih pravokotnih ploskev in dveh vzporednih pravokotnih osnov. Naj bo višina prizme h, dolžina in širina njene pravokotne osnove pa l oziroma w .

Obseg pravokotne osnove (P) = vsota njegovih štirih strani = 2 (l + š)

Ploščina pravokotne osnove (A) = dolžina × širina = l × š

Vemo, da je splošna formula za stransko površino desne prizme L. S. A. = PH, kjer je P osnovni obseg, A pa osnovna ploščina.

Z zamenjavo vseh vrednosti v splošni formuli dobimo ,

Stranska površina pravokotne prizme = 2h(l + w) kvadratnih enot

kje,

l je dolžina

w je širina

h je višina

Vemo, da je splošna formula za celotno površino desne prizme T. S. A. = PH+2A, kjer je P osnovni obseg, A osnovna površina in H višina prizme.

Z zamenjavo vseh vrednosti v splošni formuli dobimo

Celotna površina pravokotne prizme = 2h(l + w) + 2(l × w)

= 2 LH + 2 WH + 2 LW

Skupna površina pravokotne prizme = 2 (lh + wh + lw) kvadratni enoti

kje,

l je dolžina

w je širina

h je višina

Kvadratna prizma

Prizma s kvadratno osnovo se imenuje kvadratna prizma. Kvadratna prizma je sestavljena iz štirih pravokotnih ploskev in dveh vzporednih kvadratnih osnov. Naj bo višina prizme h in dolžine njenih kvadratnih osnov s.

Obseg kvadratne osnove (P) = vsota njegovih štirih strani = s + s + s + s = 4s

Površina kvadratne osnove (A) = (dolžina stranice)²= s²

Vemo, da je splošna formula za stransko površino desne prizme L. S. A. = PH, kjer je P osnovni obseg, A pa osnovna ploščina.

Z zamenjavo vseh vrednosti v splošni formuli dobimo,

Bočna površina kvadratne prizme = 4 sh kvadratnih enot

kje,

s je stranica kvadratne osnove

h je višina kvadratne prizme

Vemo, da je splošna formula za skupno površino desne prizme T. S. A. = PH+2A, kje P je osnovni obseg, A je osnovna ploščina in H je višina prizme.

Z zamenjavo vseh vrednosti v splošni formuli dobimo

Skupna površina kvadratne prizme = [4sh + 2s ² ] kvadratnih enot

kje,

s je stranica kvadratne osnove

h je višina kvadratne prizme

Peterokotna prizma

Prizma s peterokotno osnovo se imenuje peterokotna prizma. Pentagonalna prizma je sestavljena iz petih nagnjenih pravokotnih ploskev in dveh vzporednih peterokotnih baz. Naj bo h višina peterokotne prizme; a in b sta dolžini apotema in dolžini stranic peterokotnih osnov.

Obseg osnove peterokotnika (P) = vsota njegovih petih strani = 5b

Ploščina osnove peterokotnika (A) = 5/2 x (dolžina apotema) x (dolžina stranice) = 5ab

Vemo, da je splošna formula za stransko površino desne prizme L. S. A. = PH, kjer je P osnovni obseg, A pa osnovna ploščina.

Z zamenjavo vseh vrednosti v splošni formuli dobimo,

Bočna površina peterokotne prizme = 5bh kvadratnih enot

kje,

b je stranica peterokotne osnove

h je višina peterokotne prizme

Vemo, da je splošna formula za celotno površino desne prizme T. S. A. = PH+2A, kjer je P osnovni obseg, A osnovna površina in H višina prizme.

Z zamenjavo vseh vrednosti v splošni formuli dobimo,

Skupna površina peterokotne prizme = [5bh + 5ab] kvadratnih enot

kje,

b je stranica peterokotne osnove

a je dolžina apoteme.

h je višina peterokotne prizme

Šesterokotna prizma

Prizma s šesterokotno osnovo se imenuje šestkotna prizma. Heksagonalna prizma je sestavljena iz šestih nagnjenih pravokotnih ploskev in dveh vzporednih šesterokotnih baz. Naj bo h višina šesterokotne prizme; a so dolžine stranic šesterokotnih osnov.

Obseg osnove šestkotnika (P) = vsota njegovih šestih stranic = 6a

Ploščina osnove šesterokotnika (A) = 6 x (ploščina enakostraničnega trikotnika)

A = 6 x (√3a²/4) ⇒ A = 3√3a²/2

Vemo, da je splošna formula za stransko površino desne prizme L. S. A. = PH, kjer je P osnovni obseg, A pa osnovna ploščina.

Z zamenjavo vseh vrednosti v splošni formuli dobimo,

Bočna površina šesterokotne prizme = 6ah kvadratnih enot

kje,

a je stranica šesterokotne osnove

h je višina šesterokotne osnove

Vemo, da je splošna formula za celotno površino desne prizme T. S. A. = PH+2A, kjer je P osnovni obseg, A osnovna površina in H višina prizme.

Z zamenjavo vseh vrednosti v splošni formuli dobimo

Celotna površina šesterokotne prizme = [6ah +3√3a²] kvadratnih enot

kje,

a je stranica šesterokotne osnove

h je višina šesterokotne osnove:

Formula za površino prizme

Spodnja tabela podaja formulo za različne vrste prizem:

Površina prizme Rešeni primeri

Problem 1: Kolikšna je višina prizme, katere osnovna površina je 36 kvadratnih enot, njen osnovni obseg 24 enot in njena skupna površina 320 kvadratnih enot?

rešitev:

Podani podatki,

Osnovna površina = 36 kvadratnih enot

Osnovni obseg = 24 enot

Skupna površina prizme = 320 kvadratnih enot

Imamo,

Skupna površina prizme = (2 × osnovna površina) + (osnovni obseg × višina)

⇒ 320 = (2 × 36)+ (24 × h)

⇒ 24h = 248 ⇒ h = 10,34 enot

Torej je višina dane prizme 10,34 enote.

2. naloga: Poiščite skupno površino kvadratne prizme, če sta višina prizme 13 cm in dolžina stranice kvadratne osnove 4 cm.

rešitev:

Podani podatki,

Višina kvadratne prizme (h) = 13 cm

Dolžina stranice osnovnega kvadrata (a) = 4 cm

Vemo, da

Celotna površina kvadratne prizme = 2a²+ 4ah

= 2 × (4)²+ 4 × 4 × 13

= 32 + 208 = 240 cm²

Torej je skupna površina dane prizme 240 kvadratnih cm.

3. naloga: Določite osnovno dolžino peterokotne prizme, če je njena skupna površina 100 kvadratnih enot, višina in dolžina apotema pa 8 enot oziroma 5 enot.

rešitev:

Podani podatki,

Skupna površina peterokotne prizme = 100 kvadratnih enot

Višina prizme (h) = 8 enot

Dolžina apoteme (a) = 5 enot

Vemo, da

Celotna površina peterokotne prizme = 5ab + 5bh

⇒ 100 = 5b (a+ h)

⇒ 100/5 = b (5 + 8)

⇒ 20 = b × (13) ⇒ b = 25/16 = 1,54 enote

Zato je osnovna dolžina 1,54 enote

Problem 4: Določite višino pravokotne prizme in celotno ploščino pravokotne prizme, če je njena stranska površina 540 kvadratnih cm, dolžina in širina osnove pa 13 cm oziroma 7 cm.

rešitev:

Podani podatki,

Dolžina pravokotne osnove (l) = 13 cm

Širina pravokotne podlage (š) = 7 cm

Stranska površina prizme = 540 kvadratnih cm

Imamo,

'kaj je 10 od 100'

Stranska površina prizme = osnovni obseg × višina

⇒ 540 = 2 (d + š) v

⇒ 2 (13 + 7) h = 540

⇒ 2 (20) h = 540 ⇒ h = 13,5 cm

Vemo, da

Celotna površina pravokotne prizme = 2 (lw + wh + lh)

= 2 × (13 × 7 + 7 × (13,5) + 13 × (13,5))

= 2 × (91 + 94,5 + 175,5) = 722 kvadratnih cm

Torej sta višina in skupna površina dane pravokotne prizme 13,5 cm oziroma 722 kvadratnih cm.

Problem 5: Določite površino pravilne šestkotne prizme, če je višina prizme 12 in dolžina stranice podnožja 5 in.

rešitev:

Podani podatki,

Višina prizme (h) = 12 in

Dolžina stranice podnožja (a) = 6 in

Površina pravilne šestkotne prizme = 6ah + 3√3a²

= 6 × 5 × 12 + 3√3(5)²

= 360 + 75√3

= 360 + 75 × (1,732) = 489,9 kvadratnih palcev

Torej je površina dane prizme 489,9 kvadratnih palcev.

Problem 6: Izračunajte stransko in celotno površino trikotne prizme, katere osnovni obseg je 25 palcev, osnovna dolžina in višina trikotnika sta 9 in 10 palcev, višina prizme pa je 14 palcev.

rešitev:

Podani podatki,

Višina prizme (H) = 14 palcev

Osnovni obseg prizme (P) = 25 palcev

Osnovna dolžina trikotnika = 9 palcev

Višina trikotnika = 10 palcev

Vemo, da

Stranska površina prizme = osnovni obseg × višina

= 25 × 14 = 350 kvadratnih palcev

Površina trikotne osnove (A) = ½ × osnova × višina = 1/2 × 9 × 10 = 45 kvadratnih palcev

Skupna površina trikotne prizme = 2A + PH

= 2 × 45 + 25 × 14 = 90 + 350 = 440 kvadratnih palcev

Zato sta stranska in skupna površina prizme 350 kvadratnih palcev in 440 kvadratnih palcev.

Vadbene naloge o površini prizme

1. Glede na pravokotno prizmo z dimenzijami:

• Dolžina = 6 cm
• Širina = 4 cm
• Višina = 5 cm

Izračunajte skupno površino.

2. Razmislite o trikotni prizmi z dimenzijami:

• Osnovica trikotnika = 8 cm
• Višina trikotnika = 6 cm
• Dolžina prizme = 10 cm

Poiščite skupno površino.

3. Določite površino pravilne peterokotne prizme z:

• Dolžina stranice podstavka = 7 cm
• Višina prizme = 9 cm.

4. Izračunajte površino šesterokotne prizme z:

• Stranična dolžina osnove pravilnega šestkotnika = 10 cm
• Višina prizme = 12 cm.

Površina prizme – pogosta vprašanja

Kaj je prizma v geometriji?

Prizma je tridimenzionalna oblika z dvema skladnima vzporednima osnovama in pravokotnimi ali paralelogramskimi stranskimi ploskvami, ki ju povezujeta. Prizme so v različnih oblikah, kot so pravokotne prizme, trikotne prizme in peterokotne prizme, od katerih ima vsaka edinstvene značilnosti.

Kako najdete površino prizme?

Če želite ugotoviti površino prizme, izračunajte površine vseh njenih ploskev in jih nato seštejte. Za pravokotno prizmo je formula za površino 2lw + 2lh + 2wh, kjer je l dolžina, w širina in h višina. Za druge vrste prizem, kot so trikotne ali peterokotne prizme, bodo morda potrebne dodatne formule za osnovno in stransko površino.

Kakšne so lastnosti prizme?

Prizme imajo več ključnih lastnosti:

• Imata dve skladni vzporedni bazi.
• Vse stranske ploskve so paralelogrami.
• Nadmorska višina (višina) je pravokotna razdalja med dvema osnovama.
• Podstavki so po obliki in velikosti enaki.
• Prerez, vzporeden z bazami, je vedno enake oblike in velikosti kot baze.

Kateri so nekateri resnični primeri prizem?

Prizme lahko najdemo v različnih vsakdanjih predmetih in strukturah. Primeri vključujejo:

• Pravokotne prizme: Zgradbe, škatle z žitom, knjige.
• Trikotne prizme: Strehe hiš, klinasti predmeti.
• Pentagonalne prizme: nekatere vrste stebrov, nekatere arhitekturne strukture.
• Heksagonalne prizme: Določene vrste kristalov, nekatere embalaže.

Zakaj je površina prizm pomembna?

Površina je pri prizmah ključnega pomena, saj predstavlja skupno površino vseh površin (ploskev) prizme. Razumevanje površine pomaga pri različnih praktičnih aplikacijah, kot je izračun količine materiala, potrebnega za izdelavo ali prekrivanje predmeta v obliki prizme, določanje hitrosti prenosa toplote in optimizacija oblikovanja embalaže.