Trenje je sila, ki se upira relativnemu gibanju in se pojavlja na meji med telesi, pa tudi znotraj teles, kot v primeru tekočin. Koncept koeficienta trenja je prvi oblikoval Leonardo da Vinci. Velikost koeficienta trenja določajo lastnosti površin, okolice, lastnosti površine, prisotnost maziva itd.
Zakoni trenja
Obstaja pet zakonov trenja in ti so:
• Trenje premikajočega se predmeta je sorazmerno in pravokotno na normalno silo.
• Trenje, ki ga ima predmet, je odvisno od narave površine, s katero je v stiku.
• Trenje je neodvisno od območja stika, dokler obstaja območje stika.
• Kinetično trenje ni odvisno od hitrosti.
• Koeficient statičnega trenja je večji od koeficienta kinetičnega trenja.
Ko vidimo kateri koli predmet, lahko vidimo gladko površino, ko pa isti predmet pogledamo pod mikroskopom, lahko vidimo, da ima celo gladek predmet grobe robove. Skozi mikroskop je mogoče videti majhne gričke in utore, ki so znani kot nepravilnosti na površini. Torej, ko se en predmet premakne čez drugega, se te nepravilnosti na površini zapletejo in povzročijo trenje. Več bo hrapavosti, več bo nepravilnosti in večja bo uporabljena sila.
Statično trenje
Obstaja več teorij o vzrokih statičnega trenja in kot večina konceptov, povezanih s trenjem, se vsaka izkaže za veljavno pod določenimi pogoji, vendar ne uspe pod drugimi okoliščinami. Za aplikacije v realnem svetu (zlasti tiste, povezane z industrijskimi stroji in gibanjem). Dve najširše sprejeti teoriji o statičnem trenju sta povezani z mikroskopsko hrapavostjo površin.
Ne glede na to, kako popolno je površina strojno obdelana, obdelana in očiščena, bo neizogibno imela neravnine – v bistvu hrapavost, sestavljeno iz vrhov in dolin, podobno kot gorovje. (Tehnično so vrhovi neravnine.) Ko sta dve površini v stiku, se lahko zdi, da imata veliko, natančno definirano območje stika, vendar v resnici pride do stika le na določenih mestih – tj., kjer so neravnine obe površini se motita.
Vsota teh majhnih površin stika med neravninami se imenuje realna ali efektivna površina stika. Ker so ta posamezna stična območja zelo majhna, je tlak (tlak = sila ÷ površina) med površinami na teh točkah zelo visok. Ta ekstremni pritisk omogoča adhezijo med površinami s postopkom, znanim kot hladno varjenje, ki poteka na molekularni ravni. Preden se površine lahko premaknejo relativno druga proti drugi, je treba prekiniti vezi, ki povzročajo ta oprijem.
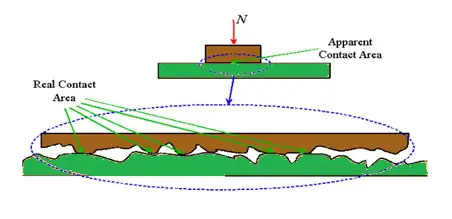
Poleg tega hrapavost površin pomeni, da se bodo na nekaterih mestih neravnine ene površine usedle v vdolbine druge površine – z drugimi besedami, površine se bodo povezale.
Ta prepletena območja je treba zlomiti ali plastično deformirati, preden se lahko površine premaknejo. Z drugimi besedami, pride do abrazije. Tako je v večini aplikacij statično trenje posledica adhezije in abrazije kontaktnih površin.
Zakoni statičnega trenja
Obstajata dva zakona statičnega trenja:
- Prvi zakon: Največja sila statičnega trenja ni odvisna od površine stika.
- Drugi zakon: Največja sila statičnega trenja je primerljiva z normalno silo, tj. če se normalna sila poveča, se poveča tudi največja zunanja sila, ki jo lahko predmet prenese, ne da bi se premaknil.

Izpeljava formule statičnega trenja
Vzemimo blok s težo mg, ki leži na vodoravni površini, kot je prikazano na sliki. Ko telo pritisne na površino, se površina deformira, tudi če je videti toga. Deformirana površina potiska telo z normalno silo R, ki je pravokotna na površino. To se imenuje normalna reakcijska sila. Uravnava mg, tj
R = mg
Zdaj pa pomislimo, da na blok deluje sila P. Jasno je, da telo ostane v mirovanju, ker neka druga sila F nastopi v vodoravni smeri in nasprotuje uporabljeni sili P, kar ima za posledico skupno silo na telo nič. Ta sila F, ki deluje vzdolž površine telesa v stiku s površino mize, se imenuje sila trenja.
Torej, dokler se telo ne premakne, je F = P. To pomeni, da če povečamo P, se poveča tudi trenje F, ki vedno ostane enako P.
Ta sila trenja, ki nastopi, dokler se dejansko gibanje ne začne, je znana kot statično trenje.
Koeficient statičnega trenja
Statično trenje je trenje, ki se pojavi, ko predmet položimo na površino. In kinetično trenje je posledica gibanja predmeta na površini. Trenje je dobro označeno s koeficientom trenja in je razloženo kot razmerje med silo trenja in normalno silo. To pomaga predmetu, da leži na površini. Koeficient statičnega trenja je skalarna količina in jo označujemo z μs.
Formula za koeficient statičnega trenja je izražena kot
mu_{s} = frac{F}{N} Kje
m s = koeficient statičnega trenja
F = statična torna sila
n = normalna sila

Kinetično trenje
Kinetično trenje je definirano kot sila, ki deluje med premikajočimi se površinami. Na telo, ki se premika po površini, deluje sila v nasprotni smeri njegovega gibanja. Velikost sile bo odvisna od koeficienta kinetičnega trenja med materialoma.
Trenje zlahka definiramo kot silo, ki zadržuje drseči predmet. Kinetično trenje je del vsega in ovira gibanje dveh ali več predmetov. Sila deluje v nasprotni smeri od tiste, na katero predmet želi zdrsniti.
Če se mora avto ustaviti, zaviramo in ravno tu nastopi trenje. Med hojo, ko se hočemo nenadoma ustaviti, se spet zahvalimo trenju. Ko pa se moramo ustaviti sredi luže, postanejo stvari težje, saj je trenja manj in človeku ne more toliko pomagati.

Premagovanje statičnega trenja med dvema površinama v bistvu odstrani tako molekularne ovire (hladno varjenje med neravninami) kot do neke mere tudi mehanske ovire (interferenca med neravninami in vdolbinami površin) za gibanje. Ko se gibanje začne, se nekaj abrazije še naprej pojavlja, vendar na veliko nižji ravni kot med statičnim trenjem, relativna hitrost med površinama pa ne zagotavlja dovolj časa za dodatno hladno varjenje (razen v primeru izjemno nizke hitrosti).
Ker je večina adhezije in abrazije premagana, da se povzroči gibanje, se upor gibanja med površinami zmanjša in površine se zdaj premikajo pod vplivom kinetičnega trenja, ki je veliko nižje od statičnega trenja.
Zakoni kinetičnega trenja
Obstajajo štirje zakoni kinetičnega trenja:
- Prvi zakon: Sila kinetičnega trenja (Fk) je neposredno sorazmeren z normalno reakcijo (N) med dvema površinama v stiku. Kje, m k = konstanta, imenovana koeficient kinetičnega trenja.
- Drugi zakon: Sila kinetičnega trenja ni odvisna od oblike in navidezne površine površin v stiku.
- Tretji zakon: Odvisno je od narave in materiala površine v stiku.
- Četrti zakon: Ni odvisna od hitrosti predmeta v stiku, če relativna hitrost med predmetom in površino ni prevelika.

Formula kinetičnega trenja
Koeficient kinetičnega trenja je označen z grško črko mu ( m ), z indeksom k. Sila kinetičnega trenja je m k krat normalna sila na telo. Izražena je v Newtonih (N).
Enačbo kinetičnega trenja lahko zapišemo kot:
Sila kinetičnega trenja = (koeficient kinetičnega trenja) (normalna sila)
F k = m k h
Kje,
F k = sila kinetičnega trenja
m k koeficient kinetičnega trenja
h = normalna sila (grška črka eta)

Izpeljava formule za kinetično trenje
Razmislimo o bloku teže mg leži na vodoravni površini, kot je prikazano na sliki. Ko telo pritisne na površino, se površina deformira, tudi če je videti toga. Deformirana površina potiska telo z normalno silo R ki je pravokotna na površino. To se imenuje normalna reakcijska sila. Uravnava mg, tj R = mg .
preklopna metoda java
Zdaj pa to silo obravnavajmo p se uporablja na bloku, kot je prikazano. Jasno je, da telo miruje zaradi neke druge sile F nastopi v vodoravni smeri in nasprotuje uporabljeni sili p kar ima za posledico neto silo na telo nič. Ta sila F, ki deluje vzdolž površine telesa v stiku s površino mize, se imenuje sila trenja .
Torej, dokler se telo ne premakne F = P . To pomeni, da če povečamo P, se poveča tudi trenje F, ki vedno ostane enako P.
Ko povečamo uporabljeno silo nekoliko nad omejitvijo trenja, se začne dejansko gibanje. To ne pomeni, da je trenje izginilo. Pomeni le, da je sila premagala omejevalno trenje. Ta sila trenja na tej stopnji je znana kot kinetično trenje ali dinamično trenje.
Kinetično ali dinamično trenje je nasprotna sila, ki nastopi, ko se telo dejansko premika po površini drugega telesa.
Uporaba statičnega in kinetičnega trenja

Uporaba statičnega trenja
Nekaj resničnih primerov statičnega trenja je navedenih v spodnjih točkah:
- Papirji na mizni plošči
- Brisača, ki visi na stojalu
- Zaznamek v knjigi
- Avto parkiran na hribu
Uporaba kinetičnega trenja
Nekaj resničnih primerov kinetičnega trenja je navedenih v spodnjih točkah.
- Trenje igra pomembno vlogo tudi v vsakdanjih dogodkih, na primer med drgnjenjem dveh predmetov. Nastalo gibanje se pretvori v toploto in tako v nekaterih primerih povzroči požar.
- Odgovorno je tudi za obrabo in zato potrebujemo olje za mazanje delov strojev, saj zmanjšuje trenje.
- Ko se dva predmeta drgneta drug ob drugega, se sila trenja pretvori v toplotno energijo, kar v redkih primerih povzroči požar
- Kinetično trenje je odgovorno za obrabo delov stroja, zato je pomembno, da dele stroja namažete z oljem.
Razlika med statičnim in kinetičnim trenjem
| Statično trenje | Kinetično trenje |
| Statično trenje je trenje med dvema ali več predmeti, ki se ne premikajo drug glede na drugega | Kinetično trenje je trenje, ki je prisotno med dvema ali več predmeti, ki se gibljejo drug glede na drugega. |
| Velikost statičnega trenja je večja zaradi večje vrednosti njegovega koeficienta. | Velikost kinetičnega trenja je sorazmerno manjša zaradi nizke vrednosti njegovega koeficienta. |
Enačba, ki predstavlja statično trenje, je podana z Fs= msh | Enačba, ki predstavlja kinetično trenje, je podana z Fk= mkh |
| Njegova vrednost je lahko nič. | Njegova vrednost nikoli ne more biti enaka nič. |
| Primer - svinčnik na mizi. | Primer – premikanje svinčnika po mizi. |
Vzorci problemov, ki temeljijo na statičnem in kinetičnem trenju
Vprašanje 1: Človek potiska po tleh veliko kartonsko škatlo z maso 75,0 kg.
rešitev:
Koeficient kinetičnega trenja je μk= 0,520
Delavec deluje s silo 400,0 N naprej.
Kakšna je velikost sile trenja?
Odgovor: Na ravno površino lahko normalno silo predmeta ugotovimo s formulo
h = mg
Z zamenjavo vrednosti η v enačbi Fk= mkη, dobimo
Fk= (0,520) (75,0 kg) (9,80 m/s2) = 382,2N
Vprašanje 2: V zgornjem vprašanju izračunajte neto silo, ki premika škatlo?
rešitev:
Skupna sila, ki deluje na telo, je vsota vseh sil, ki delujejo na telo.
V tem primeru sta sili, ki delujeta na telo, sila, s katero deluje človek, in kinetično trenje, ki deluje v nasprotni smeri.
Če se gibanje naprej šteje za pozitivno, se neto sila izračuna na naslednji način:
Fmreža= Fdelavec– Fk
Če zamenjamo vrednosti v zgornji enačbi, dobimo
Fmreža= 400 N – 382,2 N = 17,8 N
Vprašanje 3: Zakaj pri kotalnem gibanju prihaja do trenja?
odgovor:
Teoretično se žogica točkovno dotika površine.
Toda v resnici se žogica (in/ali površina) zaradi obremenitve deformira in stična površina postane eliptična.
Teoretično kotalne površine, kot so tiste, ki jih najdemo v večini rotacijskih in linearnih ležajev (razen drsnih ležajev), ne bi smele naleteti na sile trenja.
Toda v realnih aplikacijah trije dejavniki povzročajo trenje na kotalnih površinah:
1. Mikrozdrs med površinami (površine drsijo relativno druga glede na drugo)
2. Neelastične lastnosti (tj. deformacija) materialov
3. Hrapavost površin
4. vprašanje: Predmet z maso 10 kg je postavljen na gladko površino. Statično trenje med tema dvema površinama je podano kot 15 N. Poiščite koeficient statičnega trenja?
rešitev:
dano
m = 10 kg
F = 15 N
ms= ?
Vemo, da
Normalna sila, N = mg
Torej, N = 10 × 9,81 = 98,1 N
Formula za koeficient statičnega trenja je,
ms= 15/N
pomlad mvcms= 15/98,1
m s = 0,153
Vprašanje 5: Normalna sila in statična sila trenja predmeta sta 50 N oziroma 80 N. Poiščite koeficient statičnega trenja?
rešitev:
dano
N = 50 N
F = 80 N in μs= ?
Formula za koeficient statičnega trenja je
ms= F/N
ms= 80/50
ms= 1,6
Vprašanje 6: Kakšno je razmerje med statičnim in kinetičnim trenjem?
odgovor:
Sila statičnega trenja ohranja nepremični predmet v mirovanju. Ko je sila statičnega trenja premagana, je sila kinetičnega trenja tista, ki upočasni premikajoči se predmet.
Vprašanje 7: Hladilnik tehta 1619 N, koeficient statičnega trenja pa je 0,50. Kolikšna je najmanjša sila za premikanje hladilnika?
rešitev:
Podani podatki:
Teža hladilnika, W=1619 N
Š=1619 S
Koeficient statičnega trenja, μs= 0,50
Najmanjšo silo, potrebno za premikanje hladilnika, lahko podamo kot
F = msIN
F = 0,50 × 1619
F = 809,50 N.
