Rekurzivno funkcijo lahko definiramo kot rutino, ki kliče samo sebe neposredno ali posredno.

Z drugimi besedami, rekurzivna funkcija je funkcija, ki rešuje problem z reševanjem manjših primerkov istega problema. Ta tehnika se običajno uporablja pri programiranju za reševanje problemov, ki jih je mogoče razdeliti na enostavnejše, podobne podprobleme.

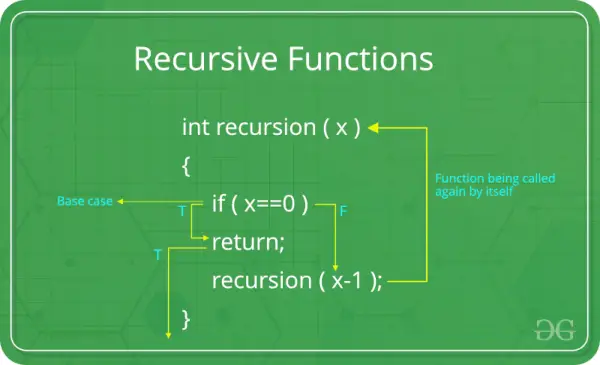
Potreba po rekurzivni funkciji:

Rekurzivna funkcija je funkcija, ki rešuje problem z reševanjem manjših primerkov istega problema. Ta tehnika se pogosto uporablja pri programiranju za reševanje problemov, ki jih je mogoče razdeliti na enostavnejše, podobne podprobleme.

algoritem združevanja

1. Reševanje kompleksnih nalog:

Rekurzivne funkcije razdelijo zapletene probleme na manjše primerke istega problema, kar povzroči kompaktno in berljivo kodo.

2. Razdeli in vladaj:

Rekurzivne funkcije so primerne za algoritme deli in vladaj, kot sta razvrščanje z združitvijo in hitro razvrščanje, razbijanje problemov na manjše podprobleme, njihovo rekurzivno reševanje in združevanje rešitev z izvirnim problemom.

css poravnava besedila

3. Sledenje nazaj :

Rekurzivno sledenje nazaj je idealno za raziskovanje in reševanje problemov, kot sta N-Queens in Sudoku.

4. Dinamično programiranje:

Rekurzivne funkcije učinkovito rešujejo probleme dinamičnega programiranja z reševanjem podproblemov in združevanjem njihovih rešitev v celovito rešitev.

5. Drevo in strukture grafov:

Rekurzivne funkcije so odlične za delo z drevesnimi in grafičnimi strukturami, poenostavljajo naloge prečkanja in prepoznavanja vzorcev .

izdelava lupinskega skripta izvršljivega

Kako napisati rekurzivno funkcijo:

Komponente rekurzivne funkcije:

Osnovni primer: Vsaka rekurzivna funkcija mora imeti osnovni primer. Osnovni primer je najpreprostejši scenarij, ki ne zahteva nadaljnje rekurzije. To je prekinitveni pogoj, ki preprečuje, da bi funkcija klicala samo sebe za nedoločen čas. Brez ustreznega osnovnega primera lahko rekurzivna funkcija vodi do neskončne rekurzije.

Rekurzivni primer: V rekurzivnem primeru funkcija pokliče samo sebe s spremenjenimi argumenti. To je bistvo rekurzije – reševanje večjega problema z razdelitvijo na manjše primerke istega problema. Rekurzivni primer bi se moral z vsako ponovitvijo približati osnovnemu primeru.

Razmislimo o primeru faktoriel števila :

V tem primeru je osnovni primer, ko n je 0 in funkcija se vrne 1 . Rekurzivni primer se množi n z rezultatom funkcije, poklicane s parametrom n – 1 . Postopek se nadaljuje, dokler ni dosežen osnovni primer.

Bistveno je zagotoviti, da ima rekurzivna funkcija pravilen osnovni primer in da rekurzivni klici vodijo do osnovnega primera, sicer se lahko postopek izvaja neomejeno dolgo, kar vodi do prelivanja sklada (presega razpoložljivega pomnilnika, dodeljenega za klice funkcij).

Spodaj je implementacija faktoriala števila:

java iterator za zemljevid

#include  using namespace std; // Recursive Function to calculate Factorial of a number int factorial(int n) {  // Base case  if (n == 0) {  return 1;  }  // Recursive case  return n * factorial(n - 1); } // Driver Code int main() {  int n = 4;  cout << 'Factorial of ' << n  << ' is:' << factorial(n);  return 0; }>

import java.util.Scanner; public class Factorial {  // Recursive Function to calculate the factorial of a number  static int factorial(int n) {  // Base case: If n is 0, the factorial is 1.  if (n == 0) {  return 1;  }  // Recursive case: Calculate the factorial by multiplying n with the factorial of (n - 1).  return n * factorial(n - 1);  }  public static void main(String[] args) {  int n = 4;  // Calculate and print the factorial of n.  int result = factorial(n);  System.out.println('Factorial of ' + n + ' is: ' + result);  } }>

# Recursive Function to calculate Factorial of a number def factorial(n): # Base case if n == 0: return 1 # Recursive case return n * factorial(n - 1) # Driver Code if __name__ == '__main__': n = 4 print('Factorial of', n, 'is:', factorial(n))>

using System; class Program {  // Recursive Function to calculate Factorial of a number  static int Factorial(int n)  {  // Base case  if (n == 0)  {  return 1;  }  // Recursive case  return n * Factorial(n - 1);  }  // Driver Code  static void Main()  {  int n = 4;  Console.WriteLine('Factorial of ' + n + ' is: ' + Factorial(n));  } }>

// Function to calculate the factorial of a number using recursion function factorial(n) {  // Base case: If n is 0, the factorial is 1.  if (n === 0) {  return 1;  }  // Recursive case: Calculate the factorial by multiplying n with the factorial of (n - 1).  return n * factorial(n - 1); } // Main function function main() {  // Given number  let n = 4;  // Calculate the factorial of n.  let result = factorial(n);  // Print the result  console.log('Factorial of ' + n + ' is: ' + result); } // Call the main function main();>

Factorial of 4 is:24>

Časovna zapletenost: O(n)
Pomožni prostor: O(n)