NFA ima lahko nič, eno ali več kot eno potezo iz danega stanja na danem vhodnem simbolu. NFA ima lahko tudi NULL poteze (poteze brez vhodnega simbola). Po drugi strani ima DFA en in samo en premik iz danega stanja na danem vhodnem simbolu.

Koraki za pretvorbo NFA v DFA:

1. korak: Pretvorite dani NFA v enakovredno prehodno tabelo
Za pretvorbo NFA v enakovredno tabelo prehodov moramo navesti vsa stanja, vhodne simbole in pravila prehoda. Pravila prehoda so predstavljena v obliki matrike, kjer vrstice predstavljajo trenutno stanje, stolpci predstavljajo vhodni simbol, celice pa predstavljajo naslednje stanje.

2. korak: Ustvarite začetno stanje DFA
Začetno stanje DFA je nabor vseh možnih začetnih stanj v NFA. Ta niz se imenuje epsilon zaprtje začetnega stanja NFA. Zaprtje epsilon je niz vseh stanj, ki jih je mogoče doseči iz začetnega stanja s sledenjem epsilon (?) prehodom.

3. korak: Ustvarite prehodno tabelo DFA
Prehodna tabela DFA je podobna prehodni tabeli NFA, vendar namesto posameznih stanj vrstice in stolpci predstavljajo nize stanj. Za vsak vhodni simbol ustrezna celica v prehodni tabeli vsebuje epsilon zaprtje nabora stanj, pridobljenih z upoštevanjem prehodnih pravil v prehodni tabeli NFA.

4. korak: Ustvarite končna stanja DFA
Končna stanja DFA so nizi stanj, ki vsebujejo vsaj eno končno stanje iz NFA.

5. korak: Poenostavite DFA
DFA, pridobljen v prejšnjih korakih, lahko vsebuje nepotrebna stanja in prehode. Za poenostavitev DFA lahko uporabimo naslednje tehnike:

• Odstrani nedosegljiva stanja: stanja, ki jih ni mogoče doseči iz začetnega stanja, lahko odstranite iz DFA.
• Odstrani mrtva stanja: stanja, ki ne morejo pripeljati do končnega stanja, je mogoče odstraniti iz DFA.
• Spoji enakovredna stanja: stanja, ki imajo enaka pravila prehoda za vse vhodne simbole, je mogoče združiti v eno samo stanje.

Korak 6: Ponavljajte korake 3-5, dokler nadaljnja poenostavitev ni več mogoča
Po poenostavitvi DFA ponavljamo korake 3-5, dokler nadaljnja poenostavitev ni več mogoča. Končni dobljeni DFA je minimiziran DFA, ki je enak danemu NFA.

primer: Razmislite o naslednjem NFA, prikazanem na sliki 1.

Sledijo različni parametri za NFA. Q = {q0, q1, q2}? = ( a, b ) F = { q2 } ? (Funkcija prehoda NFA)

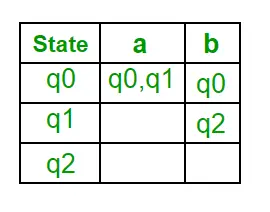
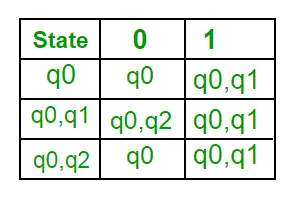
1. korak: Q’ = ? 2. korak: Q’ = {q0} 3. korak: Za vsako stanje v Q’ poiščite stanja za vsak vhodni simbol. Trenutno je stanje v Q' q0, poiščite premike od q0 na vhodnem simbolu a in b z uporabo prehodne funkcije NFA in posodobite prehodno tabelo DFA. ?’ (prehodna funkcija DFA)

Zdaj bo { q0, q1 } obravnavano kot eno samo stanje. Ker njegov vnos ni v Q', ga dodajte v Q'. Torej Q' = { q0, { q0, q1 } } Premiki iz stanja { q0, q1 } na različnih vhodnih simbolih niso prisotni v prehodni tabeli DFA, izračunali jih bomo takole: ?' ( { q0, q1 } , a ) = ? (q0, a)? ? ( q1, a ) = { q0, q1 } ?’ ( { q0, q1 }, b ) = ? (q0, b)? ? ( q1, b ) = { q0, q2 } Zdaj bomo posodobili prehodno tabelo DFA. ?’ (prehodna funkcija DFA)

Zdaj bo { q0, q2 } obravnavano kot eno samo stanje. Ker njegov vnos ni v Q', ga dodajte v Q'. Torej Q' = { q0, { q0, q1 }, { q0, q2 } } Premiki iz stanja {q0, q2} na različnih vhodnih simbolih niso prisotni v prehodni tabeli DFA, izračunali jih bomo takole: ?' ({q0, q2}, a) =? (q0, a)? ? ( q2, a ) = { q0, q1 } ?’ ( { q0, q2 }, b ) = ? (q0, b)? ? ( q2, b ) = { q0 } Zdaj bomo posodobili prehodno tabelo DFA. ?’ (prehodna funkcija DFA)

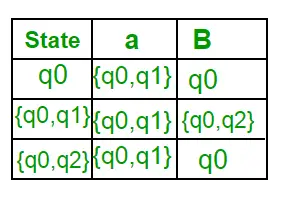
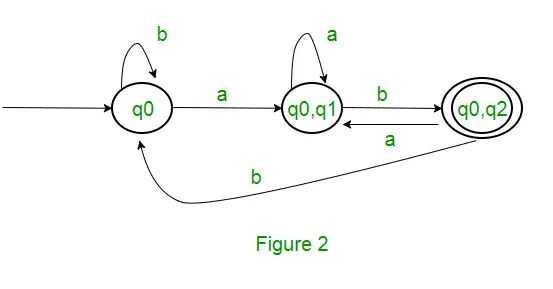
Ker ni ustvarjeno novo stanje, smo s pretvorbo končali. Končno stanje DFA bo stanje, ki ima q2 kot svojo komponento, tj. { q0, q2 } Sledijo različni parametri za DFA. Q’ = {q0, {q0, q1}, {q0, q2}}? = ( a, b ) F = { { q0, q2 } } in prehodna funkcija ?’, kot je prikazano zgoraj. Končni DFA za zgornji NFA je prikazan na sliki 2.

Opomba : Včasih ni preprosto pretvoriti regularnega izraza v DFA. Najprej lahko pretvorite regularni izraz v NFA in nato NFA v DFA.

vprašanje: Število stanj v minimalnem determinističnem končnem avtomatu, ki ustreza regularnemu izrazu (0 + 1)* (10), je ____________.

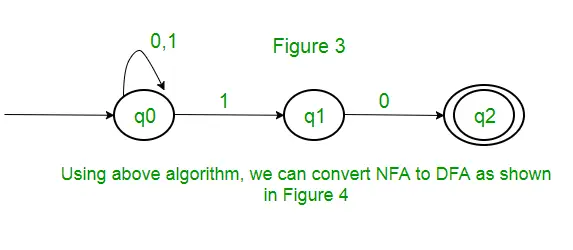
rešitev: Najprej bomo naredili NFA za zgornji izraz. Če želite narediti NFA za (0 + 1)*, bo NFA v istem stanju q0 na vhodnem simbolu 0 ali 1. Nato bomo za veriženje dodali dve potezi (q0 v q1 za 1 in q1 v q2 za 0), kot je prikazano. na sliki 3.

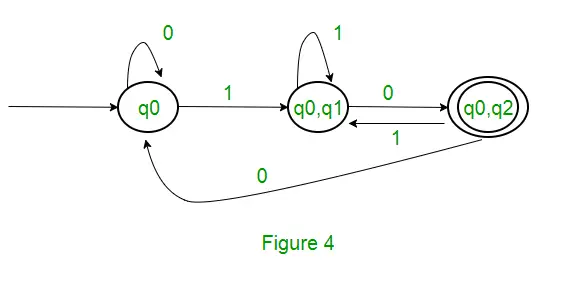
Ta članek je prispeval Sonal Tuteja.