Newtonov zakon ohlajanja je temeljni zakon, ki opisuje hitrost prenosa toplote telesa v okolico s sevanjem. Ta zakon pravi, da je hitrost, s katero telo oddaja toploto, premo sorazmerna z razliko v temperaturi telesa in okolice, glede na to, da je razlika v temperaturi majhna. to pomeni, da večja kot je razlika med temperaturo telesa in okolice, več toplote se izgubi in nižja kot je temperatura, manj toplote se izgubi. Newtonov zakon ohlajanja je poseben primer Stefan-Boltzmannovega zakona.

V tem članku bomo podrobno spoznali Newtonov zakon hlajenja, formulo Newtonovega zakona hlajenja, njegovo izpeljavo, primere in druge podrobnosti.

Definicija Newtonovega zakona hlajenja

Newton je prvi proučeval razmerje med toploto, ki jo telo izgubi v okolici. Pravi, da večja ko je razlika v temperaturi med predmetom in okolico, več toplote oddaja telo.

Newtonov zakon ohlajanja navaja, da

Hitrost izgube toplote iz telesa je premo sorazmerna z temperaturno razliko med telesom in okolico, saj temperaturna razlika ni velika.

Ta zakon se uporablja za razlago, zakaj se vroča voda ali mleko, ki ostane na mizi, ohladi hitreje kot malo toplega mleka ali vode, ki ostane na mizi. Newtonov zakon ohlajanja nam pomaga določiti temperaturo kogar koli, ne da bi jo dejansko izmerili, glede na začetno temperaturo telesa in temperaturo okolice.

Formula Newtonovega zakona o hlajenju

Formula Newtonovega zakona o hlajenju je formula za izračun temperature materiala, ko s sevanjem izgublja toploto v okolico.

Po Newtonovem zakonu ohlajanja je

Hitrost izgube toplote ( – dQ/dt) telesa je premo sorazmerna z temperaturno razliko [ΔT = (T ₂ – T ₁ )] telesa in okolice.

razvrščanje tulp python

Lahko ga predstavimo kot,

– dQ/dt ∝ (T ₂ – T ₁ )

– dQ/dt = k(T ₂ – T ₁ )

kje,
k je konstanta sorazmernosti

Z rešitvijo zgornje diferencialne enačbe dobimo,

T(t) = T _s + (T _O – T _s ) Je ^-kt

kje,
t je čas
T(t) je temperatura telesa v času t
T _s je temperatura okolice
T _O je začetna telesna temperatura
k je konstanta sorazmernosti

Izpeljava Newtonovega zakona o hlajenju

Formulo Newtonovega zakona hlajenja je mogoče izpeljati z rešitvijo diferencialne enačbe. Naj bo telo z maso m in specifično toplotno kapaciteto s pri temperaturi T₂in T₁je temperatura okolice.

Če temperatura pade za majhno količino dT ₂ pravočasno dt , potem je količina izgubljene toplote,

dQ = ms dT ₂

Stopnja izgube toplote je podana z

dQ/dt = ms (dT ₂ /dt)

Po Newtonovem zakonu ohlajanja je

– dQ/dt = k(T ₂ – T ₁ )

Primerjava zgornje enačbe

– ms (dT ₂ /dt) = k (T ₂ – T ₁ )

dT ₂ /(T ₂ –T ₁ ) = – (k / ms) dt

dT ₂ /(T ₂ – T ₁ ) = – Kdt

kje, K = k/m s

Integracija zgornje enačbe

dnevnik _je (T ₂ – T ₁ ) = – K t + c

T ₂ = T ₁ + C’ in ^–Kt

kje, C' = e ^c

Razmerje med padcem telesne temperature in časom je prikazano z grafom ohlajanja. Naklon tega grafa prikazuje hitrost padanja temperature.

samo nick

Hladilna krivulja je graf, ki prikazuje razmerje med telesno temperaturo in časom. Hitrost padanja temperature je določena z naklonom tangente na krivuljo v kateri koli točki. Spodnja slika prikazuje razmerje med padcem temperature in časom.

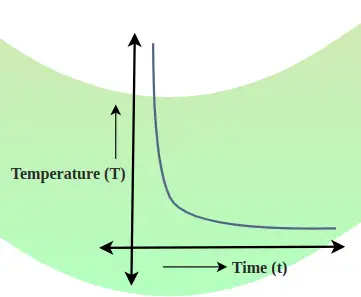
Na splošno,

T(t) = T _A +(T _H -T _A )Je ^-kt

kje
T(t) je temperatura v času t
T _A je temperatura okolice ali temperatura okolice
T _H je temperatura vročega predmeta
k je pozitivna konstanta in t je čas

Metode za uporabo Newtonovega zakona o hlajenju

Pri konstantni hitrosti ohlajanja je hitrost ohlajanja povezana s povprečno temperaturo telesa v intervalu, potem lahko izračunamo približno vrednost z uporabo Newtonovega zakona ohlajanja

dθ/dt = k(q – q _s )

kje,
q je telesna temperatura
q _s je temperatura okolice

Če je povprečna telesna temperatura q, kjer je

q = (q _jaz + q _f )/2

Preverjanje Newtonovega zakona hlajenja

Newtonov zakon ohlajanja lahko enostavno preverimo s spodaj opisanim poskusom:

Pri poskusu vzamemo posodo z dvojno steno (V) z vodo med obema stenama. V posodo z dvojno steno vzamemo bakren kalorimeter (C), ki vsebuje vročo vodo.

Uporabljamo dva termometra T₂za merjenje temperature vode v kalorimetru in T₁za merjenje temperature tople vode med dvojnimi stenami. Po enakih časovnih intervalih se zabeležita obe temperaturi in graf med dnevnikoma_je(T₂–T₁) in čas (t) je narisan kot ravna črta z negativnim naklonom.

Graf Newtonovega zakona ohlajanja

Spodaj je dodan graf Newtonovega zakona hlajenja, v tem grafu je prikazan logaritem razlike med obema temperaturama in časom.

Omejitve Newtonovega zakona hlajenja

Različne omejitve Newtonovega zakona o hlajenju so,

• Newtonov zakon ohlajanja velja, če je temperaturna razlika med telesom in okoljem majhna.
• Izguba toplote telesa je samo v obliki sevanje .
• Temperatura okolice mora med ohlajanjem telesa ostati konstantna, sicer Newtonov zakon ohlajanja ne velja.

Uporaba Newtonovega zakona o hlajenju

Različne uporabe Newtonovega zakona hlajenja so,

• Za oceno, kako dolgo bo potreben topel predmet, da se ohladi na določeno temperaturo.
• Za določanje temperature pijače v hladilniku po preteku določenega časa.
• Pomaga določiti čas smrti tako, da pogleda možno telesno temperaturo ob smrti in trenutno telesno temperaturo.

Preberi več,

• Specifična toplotna kapaciteta
• Osnovni koncept termodinamike
• Termodinamični procesi

Rešeni primeri Newtonov zakon ohlajanja

Primer 1: Ponev, napolnjena z vročo hrano, se ohladi s 94 °C na 86 °C v 2 minutah, ko je sobna temperatura 20 °C. Koliko časa bo trajalo, da se ohladi z 71 °C na 69 °C?

rešitev:

Povprečje 94 °C in 86 °C je 90 °C,

• T₂= 90 °C
• T₁= 20 °C

Spustite v tem. hrane je 8 °C v 2 minutah.

Po Newtonovem zakonu ohlajanja je

– dQ/dt = k(T ₂ –T ₁ )

8 °C /2 min = k(90 – 20)

4 = k(70) ………(1)

Povprečje 69 °C in 71 °C je 70 °C

• T₂= 70 °C
• T₁= 20 °C

Po Newtonovem zakonu ohlajanja je

2 °C /dt = k(70 – 20) ……(2)

Iz enačb (1) in (2)

cpld proti FPGA

Sprememba časa = 0,7 min = =42 s

Tako se bo hrana ohladila z 71 °C na 69 °C v 42 sekundah.

Primer 2: Telo pri temperaturi 40 °C hranimo v okolju s konstantno temperaturo 20 °C. Opaženo je, da njegova temperatura pade na 35 °C v 10 minutah. Ugotovite, koliko časa bo še potrebno, da telo doseže temperaturo 30 °C.

rešitev:

podano,

• q_jaz= (40 – 20)ºC
• q_f= (35 – 20)ºC

Po Newtonovem zakonu ohlajanja

q _f = q _jaz je ^-kt

Zdaj pa interval, v katerem temperatura pade s 40 ºC na 35 ºC.

(35 – 20) = (40 – 20) in^-(10k)

je^-10k= 3/4

-10k = (ln 4/3)

k = 0,2876/10

k = 0,02876

Zdaj ponovno uporabljam Newonovo formulo,

(30 – 20) = (35 – 20)e^-kt

10 = 15e^-kt

je^-kt= 23

-kt = ln(2/3)

t = 0,40546/k

Z uporabo vrednosti k,

t = 0,40546/0,02876

t = 14,098 min

Tako je čas, ki ga telo potrebuje, da doseže temperaturo 30 °C, 14,098 min.

Primer 3: Olje segrejemo na 70 ºC. Po 6 minutah se ohladi na 50 ºC. Izračunajte čas, potreben, da se olje ohladi s 50 ºC na 40 ºC glede na temperaturo okolice T _s = 25 ºC

rešitev:

podano,

Temperatura olja po 6 minutah, tj. T(t), je enaka 50 ºC

polje dodajanje elementov java

• Temperatura okolja T_s= 25 ºC
• Temperatura olja, T_O= 70 ºC
• Čas za ohlajanje na 50ºC = 6 min

Po Newtonovem zakonu ohlajanja je

T(t) = T_s+ (T₀– T_s) Je^-kt

{T(t) – T_s}/(T_O– T_s) = in^-kt

-kt = ln[(T(t) – T_s)/(T_O– T_s)] ………(1)

Zamenjajte vrednosti

-kt = ln[(50 – 25)/(70 – 25)]

-k = (ln 0,55556)/6

k = 0,09796

Povprečna temperatura od 50 ºC do 40 ºC je enaka 45 ºC

Ponovno uporabljam Newtonov zakon ohlajanja

-(0,09796)t = ln[(45 – 25)/(70 – 25)]

-0,09796t = ln(0,44444)

0,09796t = 0,81093

t = 0,09796/0,58778 = 8,278 min

Tako je čas, potreben, da se olje ohladi s 50 ºC na 40 ºC 8,278 min

Primer 4: Vodo segrevamo na 80 ºC 10 minut. Kolikšna bi bila njegova temperatura v stopinjah Celzija, če je k = 0,056 na minuto in je temperatura okolice 25 ºC?

rešitev:

podano,

• Temperatura okolja T_s= 25 ºC
• Temperatura vode T₀= 80 ºC
• Čas segrevanja vode (t) = 10 min
• Vrednost konstante k = 0,056.

Po Newtonovem zakonu ohlajanja je

T(t) = T_s+ (T₀– T_s) Je^-kt

Zamenjava vrednosti

T(t)= 25 + (80 – 25)e^{(0,056 × 10)}

T(t) = 25 + 55 e^{(0,056 × 10)}

T(t) = 25 + 31,42

T(t) = 56,42

Po 10 minutah bo temperatura vode 56,42 ºC.

Pogosta vprašanja o Newtonovem zakonu ohlajanja

V1: Kaj je Newtonov zakon ohlajanja?

odgovor:

Newtonov zakon hlajenja pravi, da je hitrost izgube toplote telesa premosorazmerna z temperaturno razliko med telesom in okolico.

V2: Kaj je formula Newtonovega zakona o hlajenju?

odgovor:

Formula Newtonovega zakona o hlajenju pravi, da

T(t) = T _s + (T _O – T _s ) Je ^-kt

koliko tednov v mesecu

V3: Kaj je k v Newtonovem zakonu hlajenja?

odgovor:

The k v formuli Newtonovega zakona o hlajenju je konstanta, ki je odvisna od materiala, tj. spreminjanje materiala spremeni k v Newtonovem zakonu hlajenja.

V4: Zakaj je vroče mleko lažje piti iz sklede kot iz kozarca?

odgovor:

Skleda ima večjo površino kot steklo, zato izgubi več toplote v okolico v obliki toplotnega sevanja skozi skledo in tako lažje pijemo vroče mleko iz sklede.