V resničnem svetu strojno učenje aplikacij, je običajno, da imajo veliko ustreznih funkcij, vendar jih je mogoče opaziti le podskupino. Ko imamo opravka s spremenljivkami, ki so včasih opazne in včasih ne, je res mogoče uporabiti primere, ko je ta spremenljivka vidna ali opazovana, da se naučimo in naredimo napovedi za primere, ko ni opazna. Ta pristop se pogosto imenuje obravnavanje manjkajočih podatkov. Z uporabo razpoložljivih primerov, kjer je spremenljivko mogoče opazovati, se lahko algoritmi strojnega učenja naučijo vzorcev in odnosov iz opazovanih podatkov. Te naučene vzorce je nato mogoče uporabiti za napovedovanje vrednosti spremenljivke v primerih, ko manjka ali ni opazna.
Algoritem maksimiranja pričakovanja se lahko uporablja za obravnavo situacij, ko so spremenljivke delno vidne. Ko so določene spremenljivke opazljive, lahko te primere uporabimo za učenje in oceno njihovih vrednosti. Nato lahko napovemo vrednosti teh spremenljivk v primerih, ko jih ni mogoče opazovati.
Algoritem EM so predlagali in poimenovali v temeljnem dokumentu, ki so ga leta 1977 objavili Arthur Dempster, Nan Laird in Donald Rubin. Njihovo delo je formaliziralo algoritem in pokazalo njegovo uporabnost pri statističnem modeliranju in ocenjevanju.
Algoritem EM je uporaben za latentne spremenljivke, ki so spremenljivke, ki jih ni mogoče neposredno opazovati, ampak so sklepane iz vrednosti drugih opazovanih spremenljivk. Z uporabo znane splošne oblike porazdelitve verjetnosti, ki ureja te latentne spremenljivke, lahko algoritem EM napove njihove vrednosti.
Algoritem EM služi kot osnova za mnoge nenadzorovane algoritme združevanja v gruče na področju strojnega učenja. Zagotavlja okvir za iskanje lokalnih parametrov največje verjetnosti statističnega modela in sklepanje latentnih spremenljivk v primerih, ko podatki manjkajo ali so nepopolni.
Algoritem pričakovanja-maksimizacije (EM).
Algoritem Expectation-Maximization (EM) je iterativna metoda optimizacije, ki združuje različne nenadzorovane strojno učenje algoritmi za iskanje največje verjetnosti ali največjih posteriornih ocen parametrov v statističnih modelih, ki vključujejo neopazovane latentne spremenljivke. Algoritem EM se običajno uporablja za modele latentnih spremenljivk in lahko obravnava manjkajoče podatke. Sestavljen je iz koraka ocenjevanja (E-korak) in koraka maksimizacije (M-korak), ki tvorita iterativni postopek za izboljšanje prileganja modela.
- V koraku E algoritem izračuna latentne spremenljivke, tj. pričakovanje log-verjetnosti, z uporabo trenutnih ocen parametrov.
- V koraku M algoritem določi parametre, ki povečajo pričakovano logaritemsko verjetnost, pridobljeno v koraku E, in ustrezni parametri modela se posodobijo na podlagi ocenjenih latentnih spremenljivk.

Pričakovanje-Maksimizacija v algoritmu EM
Z iterativnim ponavljanjem teh korakov skuša algoritem EM čim bolj povečati verjetnost opazovanih podatkov. Običajno se uporablja za nenadzorovane učne naloge, kot je združevanje v gruče, kjer se sklepajo o latentnih spremenljivkah in se uporablja na različnih področjih, vključno s strojnim učenjem, računalniškim vidom in obdelavo naravnega jezika.
Ključni izrazi v algoritmu maksimizacije pričakovanja (EM).
Nekateri najpogosteje uporabljeni ključni izrazi v algoritmu pričakovanja-maksimizacije (EM) so naslednji:
- Latentne spremenljivke: Latentne spremenljivke so neopazovane spremenljivke v statističnih modelih, o katerih je mogoče sklepati le posredno prek njihovih učinkov na opazovane spremenljivke. Ni jih mogoče neposredno izmeriti, lahko pa jih zaznamo z njihovim vplivom na opazovane spremenljivke. Verjetnost: je verjetnost opazovanja danih podatkov glede na parametre modela. V algoritmu EM je cilj najti parametre, ki povečajo verjetnost. Log-Likelihood: je logaritem funkcije verjetnosti, ki meri dobro prileganje med opazovanimi podatki in modelom. Algoritem EM skuša čim bolj povečati log-verjetnost. Ocena največje verjetnosti (MLE) : MLE je metoda za ocenjevanje parametrov statističnega modela z iskanjem vrednosti parametrov, ki maksimirajo funkcijo verjetnosti, ki meri, kako dobro model razlaga opazovane podatke. Posteriorna verjetnost : V kontekstu Bayesovega sklepanja je mogoče algoritem EM razširiti na oceno največjih aposteriornih (MAP) ocen, kjer se posteriorna verjetnost parametrov izračuna na podlagi predhodne porazdelitve in funkcije verjetnosti. Korak pričakovanja (E): E-korak algoritma EM izračuna pričakovano vrednost ali posteriorno verjetnost latentnih spremenljivk glede na opazovane podatke in trenutne ocene parametrov. Vključuje izračun verjetnosti vsake latentne spremenljivke za vsako podatkovno točko. Korak maksimizacije (M) : M-korak algoritma EM posodobi ocene parametrov z maksimiranjem pričakovane log-verjetnosti, pridobljene iz E-koraka. Vključuje iskanje vrednosti parametrov, ki optimizirajo funkcijo verjetnosti, običajno z metodami numerične optimizacije. Konvergenca: Konvergenca se nanaša na stanje, ko je algoritem EM dosegel stabilno rešitev. Običajno se določi s preverjanjem, ali sprememba log-verjetnosti ali ocen parametrov pade pod vnaprej določen prag.
Kako deluje algoritem pričakovanja-maksimizacije (EM):
Bistvo algoritma Expectation-Maximization je uporaba razpoložljivih opazovanih podatkov nabora podatkov za oceno manjkajočih podatkov in nato uporaba teh podatkov za posodobitev vrednosti parametrov. Podrobneje razumemo algoritem EM.
sklad v ds

Diagram poteka algoritma EM
- Inicializacija:
- Na začetku se upošteva niz začetnih vrednosti parametrov. Niz nepopolnih opazovanih podatkov je dan sistemu ob predpostavki, da opazovani podatki izvirajo iz določenega modela.
- Izračunajte posteriorno verjetnost ali odgovornost vsake latentne spremenljivke glede na opazovane podatke in trenutne ocene parametrov.
- Ocenite manjkajoče ali nepopolne vrednosti podatkov z uporabo trenutnih ocen parametrov.
- Izračunajte log-verjetnost opazovanih podatkov na podlagi trenutnih ocen parametrov in ocenjenih manjkajočih podatkov.
- Posodobite parametre modela tako, da povečate pričakovano popolno verjetnost dnevnika podatkov, pridobljeno iz E-koraka.
- To običajno vključuje reševanje težav z optimizacijo, da se najdejo vrednosti parametrov, ki maksimirajo log-verjetnost.
- Posebna uporabljena optimizacijska tehnika je odvisna od narave problema in uporabljenega modela.
- Preverite konvergenco s primerjavo spremembe log-verjetnosti ali vrednosti parametrov med ponovitvami.
- Če je sprememba pod vnaprej določenim pragom, se ustavite in upoštevajte, da je algoritem konvergiran.
- V nasprotnem primeru se vrnite na E-korak in ponavljajte postopek, dokler ne dosežete konvergence.
Implementacija algoritma pričakovanja-maksimiranja po korakih
Uvozite potrebne knjižnice
Python3
import> numpy as np> import> matplotlib.pyplot as plt> from> scipy.stats>import> norm> |
>
>
Ustvarite nabor podatkov z dvema Gaussovim komponentama
Python3
# Generate a dataset with two Gaussian components> mu1, sigma1>=> 2>,>1> mu2, sigma2>=> ->1>,>0.8> X1>=> np.random.normal(mu1, sigma1, size>=>200>)> X2>=> np.random.normal(mu2, sigma2, size>=>600>)> X>=> np.concatenate([X1, X2])> # Plot the density estimation using seaborn> sns.kdeplot(X)> plt.xlabel(>'X'>)> plt.ylabel(>'Density'>)> plt.title(>'Density Estimation of X'>)> plt.show()> |
>
>
Izhod :

Plot gostote
algoritem za hitro razvrščanje
Inicializiraj parametre
Python3
# Initialize parameters> mu1_hat, sigma1_hat>=> np.mean(X1), np.std(X1)> mu2_hat, sigma2_hat>=> np.mean(X2), np.std(X2)> pi1_hat, pi2_hat>=> len>(X1)>/> len>(X),>len>(X2)>/> len>(X)> |
>
>
Izvedite EM algoritem
- Ponavlja določeno število epoh (v tem primeru 20).
- V vsaki epohi E-korak izračuna odgovornosti (vrednosti gama) tako, da oceni Gaussove gostote verjetnosti za vsako komponento in jih ponderira z ustreznimi razmerji.
- M-korak posodobi parametre tako, da izračuna tehtano povprečje in standardni odklon za vsako komponento
Python3
zamenjaj vse
# Perform EM algorithm for 20 epochs> num_epochs>=> 20> log_likelihoods>=> []> for> epoch>in> range>(num_epochs):> ># E-step: Compute responsibilities> >gamma1>=> pi1_hat>*> norm.pdf(X, mu1_hat, sigma1_hat)> >gamma2>=> pi2_hat>*> norm.pdf(X, mu2_hat, sigma2_hat)> >total>=> gamma1>+> gamma2> >gamma1>/>=> total> >gamma2>/>=> total> > ># M-step: Update parameters> >mu1_hat>=> np.>sum>(gamma1>*> X)>/> np.>sum>(gamma1)> >mu2_hat>=> np.>sum>(gamma2>*> X)>/> np.>sum>(gamma2)> >sigma1_hat>=> np.sqrt(np.>sum>(gamma1>*> (X>-> mu1_hat)>*>*>2>)>/> np.>sum>(gamma1))> >sigma2_hat>=> np.sqrt(np.>sum>(gamma2>*> (X>-> mu2_hat)>*>*>2>)>/> np.>sum>(gamma2))> >pi1_hat>=> np.mean(gamma1)> >pi2_hat>=> np.mean(gamma2)> > ># Compute log-likelihood> >log_likelihood>=> np.>sum>(np.log(pi1_hat>*> norm.pdf(X, mu1_hat, sigma1_hat)> >+> pi2_hat>*> norm.pdf(X, mu2_hat, sigma2_hat)))> >log_likelihoods.append(log_likelihood)> # Plot log-likelihood values over epochs> plt.plot(>range>(>1>, num_epochs>+>1>), log_likelihoods)> plt.xlabel(>'Epoch'>)> plt.ylabel(>'Log-Likelihood'>)> plt.title(>'Log-Likelihood vs. Epoch'>)> plt.show()> |
>
>
Izhod :

Epoha proti log-verjetnosti
Narišite končno ocenjeno gostoto
Python3
# Plot the final estimated density> X_sorted>=> np.sort(X)> density_estimation>=> pi1_hat>*>norm.pdf(X_sorted,> >mu1_hat,> >sigma1_hat)>+> pi2_hat>*> norm.pdf(X_sorted,> >mu2_hat,> >sigma2_hat)> plt.plot(X_sorted, gaussian_kde(X_sorted)(X_sorted), color>=>'green'>, linewidth>=>2>)> plt.plot(X_sorted, density_estimation, color>=>'red'>, linewidth>=>2>)> plt.xlabel(>'X'>)> plt.ylabel(>'Density'>)> plt.title(>'Density Estimation of X'>)> plt.legend([>'Kernel Density Estimation'>,>'Mixture Density'>])> plt.show()> |
dedovanje v c++
>
>
Izhod :
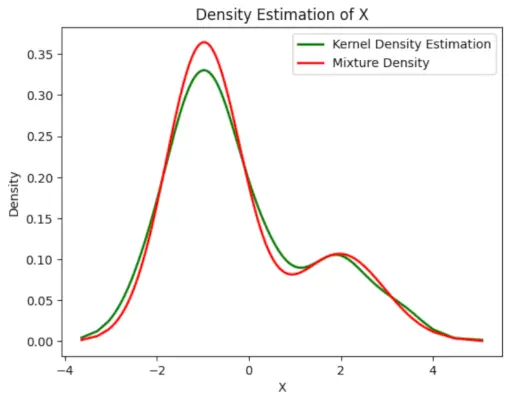
Ocenjena gostota
Aplikacije za EM algoritem
- Lahko se uporablja za dopolnitev manjkajočih podatkov v vzorcu.
- Lahko se uporablja kot osnova za nenadzorovano učenje grozdov.
- Uporablja se lahko za ocenjevanje parametrov skritega Markovega modela (HMM).
- Uporablja se lahko za odkrivanje vrednosti latentnih spremenljivk.
Prednosti EM algoritma
- Vedno je zagotovljeno, da se bo verjetnost povečala z vsako ponovitvijo.
- E-korak in M-korak sta pogosto precej enostavna za številne težave v smislu izvajanja.
- Rešitve M-korakov pogosto obstajajo v zaprti obliki.
Slabosti EM algoritma
- Ima počasno konvergenco.
- Omogoča konvergenco le lokalnim optimumom.
- Zahteva obe verjetnosti, naprej in nazaj (numerična optimizacija zahteva samo vnaprejšnjo verjetnost).
