Luhnov algoritem, znan tudi kot modul 10 oz proti 10 algoritem, je preprosta formula kontrolne vsote, ki se uporablja za potrditev različnih identifikacijskih številk, kot so številke kreditnih kartic, številke IMEI, številke kanadskega socialnega zavarovanja. Formulo LUHN je v poznih šestdesetih letih ustvarila skupina matematikov. Kmalu zatem so jo sprejela podjetja s kreditnimi karticami. Ker je algoritem v javni domeni, ga lahko uporablja vsak. Večina kreditnih kartic in številne državne identifikacijske številke uporabljajo algoritem kot preprosto metodo za razlikovanje veljavnih številk od napačno vnesenih ali kako drugače napačnih številk. Zasnovan je bil za zaščito pred naključnimi napakami, ne zlonamernimi napadi.
Koraki, vključeni v Luhnov algoritem
Razumejmo algoritem s primerom:
Razmislite o primeru številke računa 79927398713 .
Korak 1 – Začenši s skrajno desno števko, podvojite vrednost vsake druge števke,
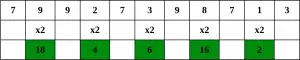
2. korak – Če podvojitev števila povzroči dvomestno število, tj. večje od 9 (npr. 6 × 2 = 12), potem seštejte števke produkta (npr. 12: 1 + 2 = 3, 15: 1 + 5 = 6), da dobimo enomestno število.

3. korak – Zdaj vzemite vsoto vseh števk.
velikosti čajne žličke

4. korak – Če je vsota modula 10 enaka 0 (če se vsota konča na nič), je število veljavno po Luhnovi formuli; drugače ne velja.

Ker je vsota 70, kar je večkratnik 10, je številka računa morda veljavna.
Ideja je preprosta; prečkamo od konca. Za vsako drugo števko jo podvojimo, preden jo dodamo. Dve števki števila, dobljenega s podvojitvijo, seštejemo.
Izvedba:
C++
// C++ program to implement Luhn algorithm> #include> using> namespace> std;> // Returns true if given card number is valid> bool> checkLuhn(>const> string& cardNo)> {> >int> nDigits = cardNo.length();> >int> nSum = 0, isSecond =>false>;> >for> (>int> i = nDigits - 1; i>= 0; i--) {> >int> d = cardNo[i] ->'0'>;> >if> (isSecond ==>true>)> >d = d * 2;> >// We add two digits to handle> >// cases that make two digits after> >// doubling> >nSum += d / 10;> >nSum += d % 10;> >isSecond = !isSecond;> >}> >return> (nSum % 10 == 0);> }> // Driver code> int> main()> {> >string cardNo =>'79927398713'>;> >if> (checkLuhn(cardNo))> >printf>(>'This is a valid card'>);> >else> >printf>(>'This is not a valid card'>);> >return> 0;> }> |
>
>
Java
// Java program to implement> // Luhn algorithm> import> java.io.*;> class> GFG {> > // Returns true if given> // card number is valid> static> boolean> checkLuhn(String cardNo)> {> >int> nDigits = cardNo.length();> >int> nSum =>0>;> >boolean> isSecond =>false>;> >for> (>int> i = nDigits ->1>; i>=>0>; i--)> >{> >int> d = cardNo.charAt(i) ->'0'>;> >if> (isSecond ==>true>)> >d = d *>2>;> >// We add two digits to handle> >// cases that make two digits> >// after doubling> >nSum += d />10>;> >nSum += d %>10>;> >isSecond = !isSecond;> >}> >return> (nSum %>10> ==>0>);> }> >// Driver code> >static> public> void> main (String[] args)> >{> >String cardNo =>'79927398713'>;> >if> (checkLuhn(cardNo))> >System.out.println(>'This is a valid card'>);> >else> >System.out.println(>'This is not a valid card'>);> > >}> }> // This Code is contributed by vt_m.> |
str.replace v Javi
>
>
Python3
Fibonaccijeva serija v Javi
# Python3 program to implement> # Luhn algorithm> # Returns true if given card> # number is valid> def> checkLuhn(cardNo):> > >nDigits>=> len>(cardNo)> >nSum>=> 0> >isSecond>=> False> > >for> i>in> range>(nDigits>-> 1>,>->1>,>->1>):> >d>=> ord>(cardNo[i])>-> ord>(>'0'>)> > >if> (isSecond>=>=> True>):> >d>=> d>*> 2> > ># We add two digits to handle> ># cases that make two digits after> ># doubling> >nSum>+>=> d>/>/> 10> >nSum>+>=> d>%> 10> > >isSecond>=> not> isSecond> > >if> (nSum>%> 10> =>=> 0>):> >return> True> >else>:> >return> False> # Driver code> if> __name__>=>=>'__main__'>:> > >cardNo>=> '79927398713'> > >if> (checkLuhn(cardNo)):> >print>(>'This is a valid card'>)> >else>:> >print>(>'This is not a valid card'>)> # This code is contributed by rutvik_56> |
>
>
C#
// C# program to implement> // Luhn algorithm> using> System;> class> GFG {> > // Returns true if given> // card number is valid> static> bool> checkLuhn(String cardNo)> {> >int> nDigits = cardNo.Length;> >int> nSum = 0;> >bool> isSecond =>false>;> >for> (>int> i = nDigits - 1; i>= 0; i--)> >{> >int> d = cardNo[i] ->'0'>;> >if> (isSecond ==>true>)> >d = d * 2;> >// We add two digits to handle> >// cases that make two digits> >// after doubling> >nSum += d / 10;> >nSum += d % 10;> >isSecond = !isSecond;> >}> >return> (nSum % 10 == 0);> }> >// Driver code> >static> public> void> Main()> >{> >String cardNo =>'79927398713'>;> >if> (checkLuhn(cardNo))> >Console.WriteLine(>'This is a valid card'>);> >else> >Console.WriteLine(>'This is not a valid card'>);> > >}> }> // This Code is contributed by vt_m.> |
>
>
Javascript
> >// Javascript program to implement Luhn algorithm> > >// Returns true if given> >// card number is valid> >function> checkLuhn(cardNo)> >{> >let nDigits = cardNo.length;> >let nSum = 0;> >let isSecond =>false>;> >for> (let i = nDigits - 1; i>= 0; i--)> >{> >let d = cardNo[i].charCodeAt() ->'0'>.charCodeAt();> >if> (isSecond ==>true>)> >d = d * 2;> >// We add two digits to handle> >// cases that make two digits> >// after doubling> >nSum += parseInt(d / 10, 10);> >nSum += d % 10;> >isSecond = !isSecond;> >}> >return> (nSum % 10 == 0);> >}> > >let cardNo =>'79927398713'>;> >if> (checkLuhn(cardNo))> >document.write(>'This is a valid card'>);> >else> >document.write(>'This is not a valid card'>);> > > |
>
>Izhod
q1 q2 q3 q4
This is a valid card>
Luhnov algoritem zazna vsako enomestno napako, pa tudi skoraj vse transpozicije sosednjih števk.
