Manj kot enako je koncept neenakosti, ki pomeni, da člen na levi strani neenakosti ne sme biti večji od člena na desni strani, tj. levi člen mora biti manjši ali največ enak desnemu členu. Članek obravnava koncept manj kot ali enako v matematiki, uvaja simbol ≤ in njegovo upodobitev na številski premici. Vključuje tabelo matematičnih simbolov, vaje in odgovore na pogosto zastavljena vprašanja o neenakosti.
Kazalo
linux, kako preimenovati imenik
- Predznak manj kot enako
- Simbol manj kot ali enako
- Manjše ali enako na številski premici
- Oznake simbolov neenakosti
- Manj kot enako in Večje kot enako
Predznak manj kot enako
Na spodnji sliki je dodan znak manj kot enako,
Kaj je manj kot ali enako?
Manj ali enako pomeni, da ena stvar ni večja od druge ali da je lahko enaka. Na primer, če imamo 2x – 3 ≤ 9, to pomeni, da dvakrat število (x) minus 3 ni večje od 9. Če poenostavimo, če dodamo 3 na obe strani, dobimo 2x ≤ 12. Nato z deljenjem obeh straneh za 2, ugotovimo, da je x ≤ 6. Torej, pravi se, da je število (x) lahko 6 ali manj, in še vedno drži.
Prav tako preverite
- Manj kot simbol
- znak enačaja
Manj kot enako Primer
Recimo, da sta Janez in Peter dva prijatelja in da je Janez star manj ali enako Petru. To pomeni, da je Janez bodisi mlajši bodisi enak Petrovi dobi. Z drugimi besedami, lahko rečemo, da je Peter ali starejši ali najmanj enak starosti Janeza.
Recimo, da je Janezova starost x let, Petrova pa 'y' let, potem lahko v obliki enačbe, ki vključuje Manj kot enako, to zapišemo kot:
x ≤ y
kje,
- x je Johnova starost
- y je Petrova doba
Simbol manj kot ali enako
Simbol manj kot ali enako. je ≤
Uporablja se v matematiki za primerjavo dveh količin. Natančneje, ko vidite a ≤ b, to pomeni, da je a manjši ali enak b. Ta simbol združuje idejo manj kot (<) in enako (=). Torej pomeni, da je vrednost na levi strani simbola manjša ali enaka vrednosti na desni strani. To pomaga izraziti razmerja med števili ali matematičnimi izrazi, kjer je lahko eno manjše od drugega ali enako.
Manj kot ali enako na številski premici
Koncept manj kot ali enako na številski premici je temeljni matematični izraz, ki se uporablja za primerjavo številskih vrednosti. V tem kontekstu pomeni, da je dano število manjše ali enako drugemu številu. Pri predstavitvi tega razmerja na številski premici je sklenjen krog (●) postavljen na točko, ki ustreza manjši ali enaki vrednosti. Na primer, x ≤ 2 je na številski premici predstavljeno takole
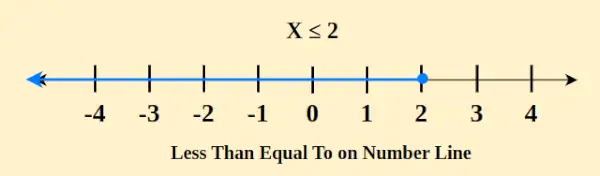
Poleg tega se od te točke desno razteza črta, ki zajema vsa števila, ki so večja ali enaka določeni vrednosti. Vključitev zaprtega kroga služi poudarjanju, da je končna točka del primerjave. Za ponazoritev, če je A ≤ B, je lahko točka A postavljena na točko B ali levo od nje na številski premici, kar pomeni, da je A manjša ali enaka B, z vključitvijo možnosti, da je A enaka B. Ta vizualna predstavitev pomaga pri razumevanju relativnih velikosti primerjanih vrednosti.
Oznake simbolov neenakosti
Spodaj so dodani različni uporabljeni znaki neenakosti skupaj z njihovim opisom:
| Zapis simbola neenakosti | |
|---|---|
| Opis simbola | Zapis simbola |
| Večji znak | > |
| Znak manj kot | < |
| Enak predznak | = |
| Ni enako predznaku | ≠ |
| Večje manj ali enako | ≥ |
| Manj ali enako | ≤ |
Manj kot enako in Večje kot enako
Spodaj navedena primerjava med Večje kot enako in Manjše enako:
| Razlika med več kot enako in manj kot enako | ||
|---|---|---|
| Vidik | Večje kot enako | Manj kot enako |
| Pomen | Označuje vrednost, ki je večja ali najmanjša od dane vrednosti | Označite vrednost, ki je manjša ali največja enaka dani vrednosti |
| Simbol | ≥ | ≤ |
| Primer | Starost Ovna je večja od 10 let ⇒ Starost Ovna ≥ 10 | Starost Rohana je manjša od 15 let ⇒ Starost Rohana ≤ 15 |
Povezano branje ,
- Večje kot manj kot
- Večje ali enako
- Neenakosti
Manj kot enako – primeri
Primer 1. Rešimo neenačbo: 3x – 5 ≤ 10.
java ustvari naključno število
rešitev:
Začnite z dodajanjem 5 na obe strani:
3x ≤ 15
Nato delite s 3: x ≤ 5
Torej je rešitev x ≤ 5
Primer 2. Rešite neenačbo: -2y + 7 ≤ 1.
rešitev:
Odštejte 7 od obeh strani: -2y ≤ -6
Delite z -2, ne pozabite obrniti znaka neenakosti: y ≥ 3
Rešitev je y ≥ 3
Manj kot enako – vadbene naloge
Preizkusite naslednje vadbene naloge, ki temeljijo na konceptu manj kot enako
Q1. Rešite neenačbo: 2y – 8 je manjše ali enako 10.
Q2. Če je m 6 in n 3, ugotovite, ali je m na kvadrat minus 5 manjše ali enako 2n plus 1.
Q3. Rešite za x: 3x plus 7 je manj kot ali enako 22.
Q4. Če je q pozitivno število, tako da je 4q minus 6 manjše ali enako 14, poiščite možne vrednosti za q.
V5. Določite obseg vrednosti za a, za katere velja, da je neenakost 2a plus 5 manjša ali enaka 15.
Manj kot enako – pogosta vprašanja
1. Kaj je manj kot ali enako?
Manj ali enako označuje razmerje med dvema vrednostma, kar pomeni, da je prva vrednost manjša ali enaka drugi.
2. Kako je Manj kot ali Enako predstavljeno na številski premici?
Na številski premici je to razmerje vizualno prikazano tako, da na številko, ki ustreza manjši ali enaki vrednosti, postavite sklenjen krog (●) in podaljšate črto v desno, ki zajema vsa števila, ki so večja ali enaka tej vrednosti.
3. Kaj pomeni zaprt krog na številski premici?
Sklenjen krog poudarja vključitev končne točke v primerjavo. Če je na primer A ≤ B, to pomeni, da je točka A na številski premici ali levo od točke B, vključno z možnostjo, da je A enako B.
4. Kakšen je primer reševanja neenačbe Manj kot ali enako?
Razmislite o neenačbi 2x – 3 ≤ 9. Če obema stranema prištejemo 3, dobimo 2x ≤ 12. Nato, če obe strani delimo z 2, dobimo x ≤ 6. Zato je rešitev neenačbe x ≤ 6.
5. Kako rešiti neenakosti, ki vključujejo manj kot ali enako?
Za reševanje neenakosti, kot je ax + b ≤ c, običajen pristop vključuje manipulacijo neenakosti s seštevanjem, odštevanjem, množenjem ali deljenjem, da izoliramo spremenljivko in določimo obseg vrednosti, ki izpolnjujejo neenakost.
6. Kaj je simbol manj kot enako in več kot enako?
Simbol manj kot enako je ≤ medtem ko je simbol večje kot enako ≥.
