Videli smo različne metode z različnimi časovnimi kompleksnostmi za izračun LCA v n-arnem drevesu:-
1. način: Naivna metoda (z izračunom poti od korena do vozlišča) | O(n) na poizvedbo
2. način: Uporaba razgradnje Sqrt | O (sqrt H)
3. način: Uporaba pristopa redke matrike DP | O (prijava)
Preučimo drugo metodo, ki ima hitrejši čas poizvedbe kot vse zgornje metode. Naš cilj bo torej izračunati LCA konstanten čas ~ O(1) . Poglejmo, kako lahko to dosežemo.
4. način: Uporaba poizvedbe za najmanjši obseg
Razpravljali smo LCA in RMQ za binarno drevo . Tukaj razpravljamo o pretvorbi problema LCA v problem RMQ za n-arno drevo.
Pre-requisites:- LCA in Binary Tree using RMQ RMQ using sparse table
Ključni koncept: S to metodo bomo naš problem LCA zmanjšali na problem RMQ (Range Minimum Query) prek statičnega polja. Ko to storimo, bomo poizvedbe za minimalni obseg povezali z zahtevanimi poizvedbami LCA.
Prvi korak bo razgradnja drevesa v ravno linearno matriko. Za to lahko uporabimo Eulerjev sprehod. Eulerjev sprehod bo dal predhodni prehod grafa. Tako bomo izvedli Eulerjev sprehod po drevesu in shranili vozlišča v matriko, ko jih obiščemo. Ta postopek zmanjša drevo > 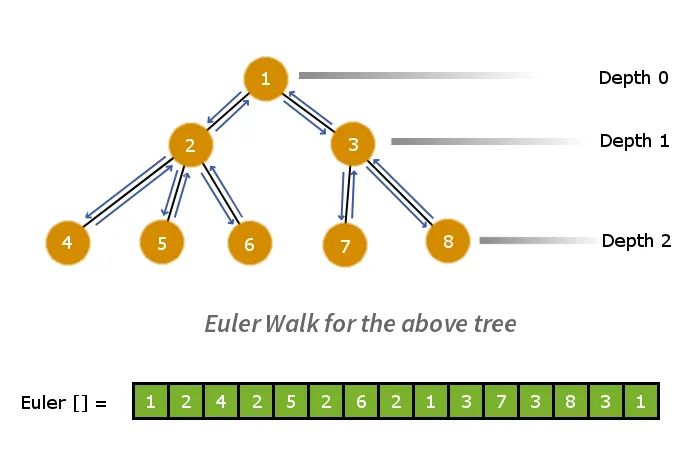
Zdaj pa razmislimo na splošno: razmislite o dveh vozliščih na drevesu. Obstajala bo natanko ena pot, ki bo povezovala obe vozlišči in vozlišče, ki ima najmanjšo vrednost globine na poti, bo LCA obeh danih vozlišč.
Zdaj vzemite kateri koli dve različni vozlišči v in v v nizu Eulerjevih sprehodov. Zdaj bodo vsi elementi na poti od u do v ležali med indeksoma vozlišč u in v v Eulerjevem nizu sprehodov. Zato moramo samo izračunati vozlišče z najmanjšo globino med indeksoma vozlišča u in vozlišča v v eulerjevem nizu.
Za to bomo vzdrževali drugo matriko, ki bo vsebovala globino vseh vozlišč, ki ustreza njihovemu položaju v Eulerjevem nizu sprehodov, da bomo lahko na njej uporabili naš algoritem RMQ.
Spodaj je podana eulerjeva niza hoje, vzporedna z nizom globinskih sledi.

jquery ta klik
Primer: - Razmislite o dveh vozliščih vozlišče 6 in vozlišče 7 v eulerjevem nizu. Za izračun LCA vozlišča 6 in 7 pogledamo najmanjšo vrednost globine za vsa vozlišča med vozliščema 6 in 7.
Zato vozlišče 1 ima najmanjšo vrednost globine = 0 in zato je LCA za vozlišča 6 in 7.

Izvedba: -
We will be maintaining three arrays 1) Euler Path 2) Depth array 3) First Appearance Index
Eulerjeva pot in niz globin sta enaka kot je opisano zgoraj
Indeks prvega nastopa FAI[] : Indeksna matrika prvega videza bo shranila indeks za prvi položaj vsakega vozlišča v matriki Eulerjeve poti. FAI[i] = prvi pojav i-tega vozlišča v nizu Euler Walk.
Izvedba zgornje metode je podana spodaj:-
Izvedba:
C++// C++ program to demonstrate LCA of n-ary tree // in constant time. #include 'bits/stdc++.h' using namespace std; #define sz 101 vector < int > adj[sz]; // stores the tree vector < int > euler; // tracks the eulerwalk vector < int > depthArr; // depth for each node corresponding // to eulerwalk int FAI[sz]; // stores first appearance index of every node int level[sz]; // stores depth for all nodes in the tree int ptr; // pointer to euler walk int dp[sz][18]; // sparse table int logn[sz]; // stores log values int p2[20]; // stores power of 2 void buildSparseTable(int n) { // initializing sparse table memset(dp-1sizeof(dp)); // filling base case values for (int i=1; i<n; i++) dp[i-1][0] = (depthArr[i]>depthArr[i-1])?i-1:i; // dp to fill sparse table for (int l=1; l<15; l++) for (int i=0; i<n; i++) if (dp[i][l-1]!=-1 and dp[i+p2[l-1]][l-1]!=-1) dp[i][l] = (depthArr[dp[i][l-1]]>depthArr[dp[i+p2[l-1]][l-1]])? dp[i+p2[l-1]][l-1] : dp[i][l-1]; else break; } int query(int lint r) { int d = r-l; int dx = logn[d]; if (l==r) return l; if (depthArr[dp[l][dx]] > depthArr[dp[r-p2[dx]][dx]]) return dp[r-p2[dx]][dx]; else return dp[l][dx]; } void preprocess() { // memorizing powers of 2 p2[0] = 1; for (int i=1; i<18; i++) p2[i] = p2[i-1]*2; // memorizing all log(n) values int val = 1ptr=0; for (int i=1; i<sz; i++) { logn[i] = ptr-1; if (val==i) { val*=2; logn[i] = ptr; ptr++; } } } /** * Euler Walk ( preorder traversal) * converting tree to linear depthArray * Time Complexity : O(n) * */ void dfs(int curint prevint dep) { // marking FAI for cur node if (FAI[cur]==-1) FAI[cur] = ptr; level[cur] = dep; // pushing root to euler walk euler.push_back(cur); // incrementing euler walk pointer ptr++; for (auto x:adj[cur]) { if (x != prev) { dfs(xcurdep+1); // pushing cur again in backtrack // of euler walk euler.push_back(cur); // increment euler walk pointer ptr++; } } } // Create Level depthArray corresponding // to the Euler walk Array void makeArr() { for (auto x : euler) depthArr.push_back(level[x]); } int LCA(int uint v) { // trivial case if (u==v) return u; if (FAI[u] > FAI[v]) swap(uv); // doing RMQ in the required range return euler[query(FAI[u] FAI[v])]; } void addEdge(int uint v) { adj[u].push_back(v); adj[v].push_back(u); } int main(int argc char const *argv[]) { // constructing the described tree int numberOfNodes = 8; addEdge(12); addEdge(13); addEdge(24); addEdge(25); addEdge(26); addEdge(37); addEdge(38); // performing required precalculations preprocess(); // doing the Euler walk ptr = 0; memset(FAI-1sizeof(FAI)); dfs(100); // creating depthArray corresponding to euler[] makeArr(); // building sparse table buildSparseTable(depthArr.size()); cout << 'LCA(67) : ' << LCA(67) << 'n'; cout << 'LCA(64) : ' << LCA(64) << 'n'; return 0; }
// Java program to demonstrate LCA of n-ary // tree in constant time. import java.util.ArrayList; import java.util.Arrays; class GFG{ static int sz = 101; @SuppressWarnings('unchecked') // Stores the tree static ArrayList<Integer>[] adj = new ArrayList[sz]; // Tracks the eulerwalk static ArrayList<Integer> euler = new ArrayList<>(); // Depth for each node corresponding static ArrayList<Integer> depthArr = new ArrayList<>(); // to eulerwalk // Stores first appearance index of every node static int[] FAI = new int[sz]; // Stores depth for all nodes in the tree static int[] level = new int[sz]; // Pointer to euler walk static int ptr; // Sparse table static int[][] dp = new int[sz][18]; // Stores log values static int[] logn = new int[sz]; // Stores power of 2 static int[] p2 = new int[20]; static void buildSparseTable(int n) { // Initializing sparse table for(int i = 0; i < sz; i++) { for(int j = 0; j < 18; j++) { dp[i][j] = -1; } } // Filling base case values for(int i = 1; i < n; i++) dp[i - 1][0] = (depthArr.get(i) > depthArr.get(i - 1)) ? i - 1 : i; // dp to fill sparse table for(int l = 1; l < 15; l++) for(int i = 0; i < n; i++) if (dp[i][l - 1] != -1 && dp[i + p2[l - 1]][l - 1] != -1) dp[i][l] = (depthArr.get(dp[i][l - 1]) > depthArr.get( dp[i + p2[l - 1]][l - 1])) ? dp[i + p2[l - 1]][l - 1] : dp[i][l - 1]; else break; } static int query(int l int r) { int d = r - l; int dx = logn[d]; if (l == r) return l; if (depthArr.get(dp[l][dx]) > depthArr.get(dp[r - p2[dx]][dx])) return dp[r - p2[dx]][dx]; else return dp[l][dx]; } static void preprocess() { // Memorizing powers of 2 p2[0] = 1; for(int i = 1; i < 18; i++) p2[i] = p2[i - 1] * 2; // Memorizing all log(n) values int val = 1 ptr = 0; for(int i = 1; i < sz; i++) { logn[i] = ptr - 1; if (val == i) { val *= 2; logn[i] = ptr; ptr++; } } } // Euler Walk ( preorder traversal) converting // tree to linear depthArray // Time Complexity : O(n) static void dfs(int cur int prev int dep) { // Marking FAI for cur node if (FAI[cur] == -1) FAI[cur] = ptr; level[cur] = dep; // Pushing root to euler walk euler.add(cur); // Incrementing euler walk pointer ptr++; for(Integer x : adj[cur]) { if (x != prev) { dfs(x cur dep + 1); // Pushing cur again in backtrack // of euler walk euler.add(cur); // Increment euler walk pointer ptr++; } } } // Create Level depthArray corresponding // to the Euler walk Array static void makeArr() { for(Integer x : euler) depthArr.add(level[x]); } static int LCA(int u int v) { // Trivial case if (u == v) return u; if (FAI[u] > FAI[v]) { int temp = u; u = v; v = temp; } // Doing RMQ in the required range return euler.get(query(FAI[u] FAI[v])); } static void addEdge(int u int v) { adj[u].add(v); adj[v].add(u); } // Driver code public static void main(String[] args) { for(int i = 0; i < sz; i++) { adj[i] = new ArrayList<>(); } // Constructing the described tree int numberOfNodes = 8; addEdge(1 2); addEdge(1 3); addEdge(2 4); addEdge(2 5); addEdge(2 6); addEdge(3 7); addEdge(3 8); // Performing required precalculations preprocess(); // Doing the Euler walk ptr = 0; Arrays.fill(FAI -1); dfs(1 0 0); // Creating depthArray corresponding to euler[] makeArr(); // Building sparse table buildSparseTable(depthArr.size()); System.out.println('LCA(67) : ' + LCA(6 7)); System.out.println('LCA(64) : ' + LCA(6 4)); } } // This code is contributed by sanjeev2552
# Python program to demonstrate LCA of n-ary tree # in constant time. from typing import List # stores the tree adj = [[] for _ in range(101)] # tracks the eulerwalk euler = [] # depth for each node corresponding to eulerwalk depthArr = [] # stores first appearance index of every node FAI = [-1] * 101 # stores depth for all nodes in the tree level = [0] * 101 # pointer to euler walk ptr = 0 # sparse table dp = [[-1] * 18 for _ in range(101)] # stores log values logn = [0] * 101 # stores power of 2 p2 = [0] * 20 def buildSparseTable(n: int): # initializing sparse table for i in range(n): dp[i][0] = i-1 if depthArr[i] > depthArr[i-1] else i # dp to fill sparse table for l in range(1 15): for i in range(n): if dp[i][l-1] != -1 and dp[i+p2[l-1]][l-1] != -1: dp[i][l] = dp[i+p2[l-1]][l-1] if depthArr[dp[i][l-1] ] > depthArr[dp[i+p2[l-1]][l-1]] else dp[i][l-1] else: break def query(l: int r: int) -> int: d = r-l dx = logn[d] if l == r: return l if depthArr[dp[l][dx]] > depthArr[dp[r-p2[dx]][dx]]: return dp[r-p2[dx]][dx] else: return dp[l][dx] def preprocess(): global ptr # memorizing powers of 2 p2[0] = 1 for i in range(1 18): p2[i] = p2[i-1]*2 # memorizing all log(n) values val = 1 ptr = 0 for i in range(1 101): logn[i] = ptr-1 if val == i: val *= 2 logn[i] = ptr ptr += 1 def dfs(cur: int prev: int dep: int): global ptr # marking FAI for cur node if FAI[cur] == -1: FAI[cur] = ptr level[cur] = dep # pushing root to euler walk euler.append(cur) # incrementing euler walk pointer ptr += 1 for x in adj[cur]: if x != prev: dfs(x cur dep+1) # pushing cur again in backtrack # of euler walk euler.append(cur) # increment euler walk pointer ptr += 1 # Create Level depthArray corresponding # to the Euler walk Array def makeArr(): global depthArr for x in euler: depthArr.append(level[x]) def LCA(u: int v: int) -> int: # trivial case if u == v: return u if FAI[u] > FAI[v]: u v = v u # doing RMQ in the required range return euler[query(FAI[u] FAI[v])] def addEdge(u v): adj[u].append(v) adj[v].append(u) # constructing the described tree numberOfNodes = 8 addEdge(1 2) addEdge(1 3) addEdge(2 4) addEdge(2 5) addEdge(2 6) addEdge(3 7) addEdge(3 8) # performing required precalculations preprocess() # doing the Euler walk ptr = 0 FAI = [-1] * (numberOfNodes + 1) dfs(1 0 0) # creating depthArray corresponding to euler[] makeArr() # building sparse table buildSparseTable(len(depthArr)) print('LCA(67) : ' LCA(6 7)) print('LCA(64) : ' LCA(6 4))
// C# program to demonstrate LCA of n-ary // tree in constant time. using System; using System.Collections.Generic; public class GFG { static int sz = 101; // Stores the tree static List<int>[] adj = new List<int>[sz]; // Tracks the eulerwalk static List<int> euler = new List<int>(); // Depth for each node corresponding static List<int> depthArr = new List<int>(); // to eulerwalk // Stores first appearance index of every node static int[] FAI = new int[sz]; // Stores depth for all nodes in the tree static int[] level = new int[sz]; // Pointer to euler walk static int ptr; // Sparse table static int[] dp = new int[sz 18]; // Stores log values static int[] logn = new int[sz]; // Stores power of 2 static int[] p2 = new int[20]; static void buildSparseTable(int n) { // Initializing sparse table for(int i = 0; i < sz; i++) { for(int j = 0; j < 18; j++) { dp[ij] = -1; } } // Filling base case values for(int i = 1; i < n; i++) dp[i - 10] = (depthArr[i] > depthArr[i - 1]) ? i - 1 : i; // dp to fill sparse table for(int l = 1; l < 15; l++) for(int i = 0; i < n; i++) if (dp[il - 1] != -1 && dp[i + p2[l - 1]l - 1] != -1) dp[il] = (depthArr[dp[il - 1]] > depthArr[dp[i + p2[l - 1]l - 1]]) ? dp[i + p2[l - 1]l - 1] : dp[il - 1]; else break; } static int query(int l int r) { int d = r - l; int dx = logn[d]; if (l == r) return l; if (depthArr[dp[ldx]] > depthArr[dp[r - p2[dx]dx]]) return dp[r - p2[dx]dx]; else return dp[ldx]; } static void preprocess() { // Memorizing powers of 2 p2[0] = 1; for(int i = 1; i < 18; i++) p2[i] = p2[i - 1] * 2; // Memorizing all log(n) values int val = 1 ptr = 0; for(int i = 1; i < sz; i++) { logn[i] = ptr - 1; if (val == i) { val *= 2; logn[i] = ptr; ptr++; } } } // Euler Walk ( preorder traversal) converting // tree to linear depthArray // Time Complexity : O(n) static void dfs(int cur int prev int dep) { // Marking FAI for cur node if (FAI[cur] == -1) FAI[cur] = ptr; level[cur] = dep; // Pushing root to euler walk euler.Add(cur); // Incrementing euler walk pointer ptr++; foreach (int x in adj[cur]) { if (x != prev) { dfs(x cur dep + 1); euler.Add(cur); ptr++; } } } // Create Level depthArray corresponding // to the Euler walk Array static void makeArr() { foreach (int x in euler) depthArr.Add(level[x]); } static int LCA(int u int v) { // Trivial case if (u == v) return u; if (FAI[u] > FAI[v]) { int temp = u; u = v; v = temp; } // Doing RMQ in the required range return euler[query(FAI[u] FAI[v])]; } static void addEdge(int u int v) { adj[u].Add(v); adj[v].Add(u); } // Driver Code static void Main(string[] args) { int sz = 9; adj = new List<int>[sz]; for (int i = 0; i < sz; i++) { adj[i] = new List<int>(); } // Constructing the described tree int numberOfNodes = 8; addEdge(1 2); addEdge(1 3); addEdge(2 4); addEdge(2 5); addEdge(2 6); addEdge(3 7); addEdge(3 8); // Performing required precalculations preprocess(); // Doing the Euler walk ptr = 0; Array.Fill(FAI -1); dfs(1 0 0); // Creating depthArray corresponding to euler[] makeArr(); // Building sparse table buildSparseTable(depthArr.Count); Console.WriteLine('LCA(67) : ' + LCA(6 7)); Console.WriteLine('LCA(64) : ' + LCA(6 4)); } } // This code is contributed by Prince Kumar
let adj = []; for (let _ = 0; _ < 101; _++) { adj.push([]); } // tracks the eulerwalk let euler = []; // depth for each node corresponding to eulerwalk let depthArr = []; // stores first appearance index of every node let FAI = new Array(101).fill(-1); // stores depth for all nodes in the tree let level = new Array(101).fill(0); // pointer to euler walk let ptr = 0; // sparse table let dp = []; for (let _ = 0; _ < 101; _++) { dp.push(new Array(18).fill(-1)); } // stores log values let logn = new Array(101).fill(0); // stores power of 2 let p2 = new Array(20).fill(0); function buildSparseTable(n) { // initializing sparse table for (let i = 0; i < n; i++) { dp[i][0] = i - 1 >= 0 && depthArr[i] > depthArr[i - 1] ? i - 1 : i; } // dp to fill sparse table for (let l = 1; l < 15; l++) { for (let i = 0; i < n; i++) { if ( dp[i][l - 1] !== -1 && dp[i + p2[l - 1]][l - 1] !== -1 ) { dp[i][l] = depthArr[dp[i][l - 1]] > depthArr[dp[i + p2[l - 1]][l - 1]] ? dp[i + p2[l - 1]][l - 1] : dp[i][l - 1]; } else { break; } } } } function query(l r) { let d = r - l; let dx = logn[d]; if (l === r) { return l; } if (depthArr[dp[l][dx]] > depthArr[dp[r - p2[dx]][dx]]) { return dp[r - p2[dx]][dx]; } else { return dp[l][dx]; } } function preprocess() { // memorizing powers of 2 p2[0] = 1; for (let i = 1; i < 18; i++) { p2[i] = p2[i - 1] * 2; } // memorizing all log(n) values let val = 1; ptr = 0; for (let i = 1; i < 101; i++) { logn[i] = ptr - 1; if (val === i) { val *= 2; logn[i] = ptr; ptr += 1; } } } function dfs(cur prev dep) { // marking FAI for cur node if (FAI[cur] === -1) { FAI[cur] = ptr; } level[cur] = dep; // pushing root to euler walk euler.push(cur); // incrementing euler walk pointer ptr += 1; for (let x of adj[cur]) { if (x !== prev) { dfs(x cur dep + 1); // pushing cur again in backtrack // of euler walk euler.push(cur); // increment euler walk pointer ptr += 1; } } } // Create Level depthArray corresponding // to the Euler walk Array function makeArr() { for (let x of euler) { depthArr.push(level[x]); } } function LCA(u v) { // trivial case if (u === v) { return u; } if (FAI[u] > FAI[v]) { [u v] = [v u]; } // doing RMQ in the required range return euler[query(FAI[u] FAI[v])]; } function addEdge(u v) { adj[u].push(v); adj[v].push(u); } // constructing the described tree let numberOfNodes = 8; addEdge(1 2); addEdge(1 3); addEdge(2 4); addEdge(2 5); addEdge(2 6); addEdge(3 7); addEdge(3 8); // performing required precalculations preprocess(); // doing the Euler walk ptr = 0; FAI = new Array(numberOfNodes + 1).fill(-1); dfs(1 0 0); // creating depthArray corresponding to euler[] makeArr(); // building sparse table buildSparseTable(depthArr.length); console.log('LCA(67) : ' LCA(6 7)); console.log('LCA(64) : ' LCA(6 4));
Izhod
LCA(67) : 1 LCA(64) : 2
Opomba: Vnaprej izračunavamo vso zahtevano moč dvojk in prav tako vnaprej izračunavamo vse zahtevane vrednosti dnevnika, da zagotovimo konstantno časovno kompleksnost na poizvedbo. Sicer, če bi naredili izračun dnevnika za vsako operacijo poizvedbe, naša časovna kompleksnost ne bi bila konstantna.
Časovna zapletenost: Postopek pretvorbe iz LCA v RMQ izvede Euler Walk, ki traja O(n) čas.
Predhodna obdelava za redko tabelo v RMQ traja O(nlogn) časa in odgovarjanje na vsako poizvedbo je proces s konstantnim časom. Zato je splošna časovna kompleksnost O(nlogn) - predprocesiranje in O(1) za vsako poizvedbo.
Pomožni prostor: O(n+s)
inicializirati seznam python
Ustvari kviz
