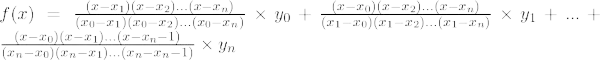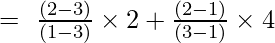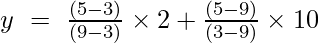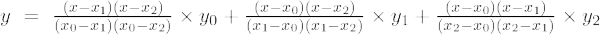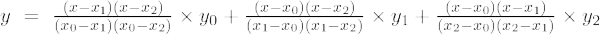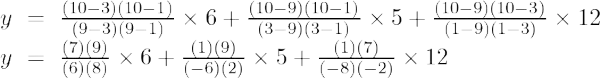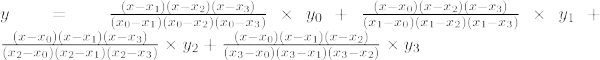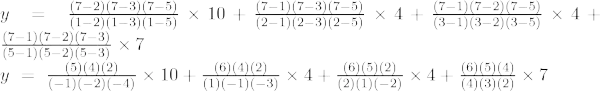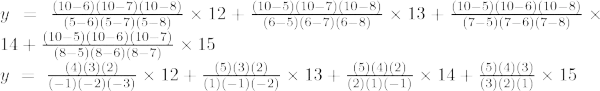LAGRANGEOVA INTERPOLACIJSKA FORMULA: DOKAZ, PRIMERI IN POGOSTA VPRAŠANJA

Lagrangeova interpolacijska formula najde polinom, imenovan Lagrangeov polinom, ki zavzame določene vrednosti na poljubni točki. Je n-ta stopnjapolinomski izraz funkcije f(x). Metoda interpolacije se uporablja za iskanje novih podatkovnih točk znotraj območja diskretnega niza znanih podatkovnih točk.

podčrtaj v oznaki

V tem članku bomo podrobno spoznali Lagrangeovo interpolacijo, Lagrangeovo interpolacijsko formulo, dokaz za Lagrangeovo interpolacijsko formulo, primere na podlagi Lagrangeove interpolacijske formule in druge.

Kaj je Lagrangeova interpolacija?

Lagrangeova interpolacija je način iskanja vrednosti katere koli funkcije na kateri koli dani točki, ko funkcija ni dana. Uporabimo druge točke na funkciji, da dobimo vrednost funkcije na kateri koli zahtevani točki.

Recimo, da imamo funkcijo y = f(x), v kateri zamenjava vrednosti x daje različne vrednosti y. In dobili smo dve točki (x₁, in₁) in (x₂, in₂) na krivulji, potem se vrednost y pri x = a (konstanta) izračuna z uporabo Lagrangeove interpolacijske formule.

Lagrangeova interpolacijska formula

Glede na nekaj realnih vrednosti x₁, x₂, x₃, …, x_nin y₁, in₂, in₃, …, in_nin tam bo polinom P z realnimi koeficienti, ki izpolnjuje pogoje P(x_jaz) = in_jaz, ∀ i = {1, 2, 3, …, n} in stopnja polinoma P mora biti manjša od števila realnih vrednosti, tj. stopnja (P)

Lagrangeova interpolacijska formula za n-ti red

Lagrangeova interpolacijska formula za n^thpolinom stopnje je podan spodaj:

Lagrangeova interpolacijska formula za n ^th red je,

$f(x)=frac{(x-x_1)(x-x_2)...(x-x_n)}{(x_0-x_1)(x_0-x_2)...(x_0-x_n)}krat y_0+ frac{(x-x_0)(x-x_2)...(x-x_n)}{(x_1-x_0)(x_1-x_2)...(x_1-x_n)}krat y_1+...+ frac{(x-x_0)(x-x_1)...(x-x_n-1)}{(x_n-x_0)(x_n-x_1)...(x_n-x_n-1)} imes y_n$

Lagrangeova interpolacijska formula prvega reda

Če jeStopnja polinoma je 1, potem se imenuje polinom prvega reda. Lagrangeova interpolacijska formula za 1^stvrstni red polinomov je,

$f(x)~=~frac{(x-x_1)}{(x_0-x_1)}krat y_0+frac{(x-x_0)}{(x_1-x_0)}krat y_1$

Lagrangeova interpolacijska formula drugega reda

Če je stopnja polinoma 2, se imenuje polinom drugega reda. Lagrangeova interpolacijska formula za polinome 2. reda je,

$f(x)~=~frac{(x-x_1)(x-x_2)}{(x_0-x_1)(x_0-x_2)}krat y_0+frac{(x-x_0)(x-x_2)} {(x_1-x_0)(x_1-x_2)}krat y_1+frac{(x-x_0)(x-x_1)}{(x_2-x_0)(x_2-x_1)}krat y_2$

Dokaz Lagrangeovega izreka

Oglejmo si polinom n-te stopnje dane oblike,

f(x) = A₀(x – x₁)(x – x₂)(x – x₃)…(x – x_n) + A₁(x – x₁)(x – x₂)(x – x₃)…(x – x_n) + … + A_(n-1)(x – x₁)(x – x₂)(x – x₃)…(x – x_n)

Nadomestna opažanja x_jazda dobim A_jaz

Postavite x = x₀potem dobimo A₀

f(x₀) = in₀= A₀(x₀– x₁)(x₀– x₂)(x₀– x₃)…(x₀– x_n)

A ₀ = in ₀ /(x ₀ – x ₁ )(x ₀ – x ₂ )(x ₀ – x ₃ )…(x ₀ – x _n )

Z zamenjavo x = x₁dobimo A₁

f(x₁) = in₁= A₁(x₁– x₀)(x₁– x₂)(x₁– x₃)…(x₁– x_n)

A ₁ = in ₁ /(x ₁ – x ₀ )(x ₁ – x ₂ )(x ₁ – x ₃ )…(x ₁ – x _n )

Podobno z zamenjavo x = x_ndobimo A_n

f(x_n) = in_n= A_n(x_n– x₀)(x_n– x₁)(x_n– x₂)…(x_n– x_n-1)

A _n = in _n /(x _n – x ₀ )(x _n – x ₁ )(x _n – x ₂ )…(x _n – x _n-1 )

Če nadomestimo vse vrednosti A_jazv funkciji f(x), kjer je i = 1, 2, 3, …n, potem dobimo Lagrangeovo interpolacijsko formulo kot,

$f(x)~=~frac{(x-x_1)(x-x_2)...(x-x_n)}{(x_0-x_1)(x_0-x_2)...(x_0-x_n)} krat y_0+frac{(x-x_0)(x-x_2)...(x-x_n)}{(x_1-x_0)(x_1-x_2)...(x_1-x_n)}krat y_1+... +frac{(x-x_0)(x-x_1)...(x-x_n-1)}{(x_n-x_0)(x_n-x_1)...(x_n-x_n-1)}krat y_n$

Lastnosti Lagrangeove interpolacijske formule

Različne lastnosti Lagrangeove interpolacijske formule so obravnavane spodaj,

Ta formula se uporablja za iskanje vrednosti funkcije na kateri koli točki, tudi če sama funkcija ni podana.
Uporablja se tudi, če navedene točke niso enakomerno razporejene.
Poda vrednost odvisne spremenljivke za katero koli neodvisno spremenljivko, ki pripada kateri koli funkciji, in se zato uporablja v numerični analizi za iskanje vrednosti funkcije itd.

Uporaba Lagrangeove interpolacijske formule

Spodaj so obravnavane različne uporabe Lagrangeove interpolacijske formule,

Uporablja se za iskanje vrednosti odvisne spremenljivke pri kateri koli določeni neodvisni spremenljivki, tudi če sama funkcija ni podana.
Uporablja se pri skaliranju slik.
Uporablja se pri modeliranju AI.
Uporablja se za poučevanje NLP itd.

Preberi več,

Interpolacijska formula
Formula za linearno interpolacijo

Primeri uporabe Lagrangeove interpolacijske formule

Oglejmo si nekaj vzorčnih vprašanj o Lagrangeovi interpolacijski formuli.

Primer 1: Poiščite vrednost y pri x = 2 za dano množico točk (1, 2), (3, 4)

rešitev:

podano,

(x₀, in₀) = (1, 2)
(x₁, in₁) = (3, 4)
Lagrangeova interpolacijska formula prvega reda je,

$y~=~frac{(x-x_1)}{(x_0-x_1)}krat y_0+frac{(x-x_0)}{(x_1-x_0)}krat y_1$

Pri x = 2

in $=~frac{(2-3)}{(1-3)}krat 2+frac{(2-1)}{(3-1)}krat 4$

y = (-2/-2) + (4/2)

y = 1 + 2 = 3

Vrednost y pri x = 2 je 3

Primer 2: Poiščite vrednost y pri x = 5 za dano množico točk (9, 2), (3, 10)

rešitev:

podano,

(x₀, in₀) = (9, 2)
(x₁, in₁) = (3, 10)
Lagrangeova interpolacijska formula prvega reda je,

$y~=~frac{(x-x_1)}{(x_0-x_1)}krat y_0+frac{(x-x_0)}{(x_1-x_0)}krat y_1$

Pri x = 5

$y~=~frac{(5-3)}{(9-3)}krat 2+frac{(5-9)}{(3-9)}krat 10$

y = (4/6) + (-40/-6)

y = (2/3) + (20/3)

y = 22/3 = 7,33

Vrednost y pri x = 5 je 7,33

Primer 3: Poiščite vrednost y pri x = 1 za dano množico točk (1, 6), (3, 4), (2, 5)

rešitev:

podano,

(x₀, in₀) = (1, 6)
(x₁, in₁) = (3, 4)
(x₂, in₂) = (2, 5)
Lagrangeova interpolacijska formula drugega reda je,

$y~=~frac{(x-x_1)(x-x_2)}{(x_0-x_1)(x_0-x_2)}krat y_0+frac{(x-x_0)(x-x_2)}{(x_1 -x_0)(x_1-x_2)}krat y_1+frac{(x-x_0)(x-x_1)}{(x_2-x_0)(x_2-x_1)}krat y_2$

Pri x = 1

$y~=~frac{(1-3)(1-2)}{(1-3)(1-2)}krat 6+frac{(1-1)(1-2)}{( 3-1)(3-2)}krat 4+frac{(1-1)(1-3)}{(2-1)(2-3)}krat 5 y~=~ frac{(-2)(-1)}{(-2)(-1)}krat 6+frac{(0)(-1)}{(2)(1)}krat 4+frac {(0)(-2)}{(1)(-1)}krat 5$

y = (12/2) + 0 + 0

y = 6

Vrednost y pri x = 1 je 6

Primer 4: Poiščite vrednost y pri x = 10 za dano množico točk (9, 6), (3, 5), (1, 12)

rešitev:

podano,

(x₀, in₀) = (9, 6)
(x₁, in₁) = (3, 5)
(x₂, in₂) = (1, 12)
Lagrangeova interpolacijska formula drugega reda je,

$y~=~frac{(x-x_1)(x-x_2)}{(x_0-x_1)(x_0-x_2)}krat y_0+frac{(x-x_0)(x-x_2)}{(x_1 -x_0)(x_1-x_2)}krat y_1+frac{(x-x_0)(x-x_1)}{(x_2-x_0)(x_2-x_1)}krat y_2$

Pri x = 10

$y~=~frac{(10-3)(10-1)}{(9-3)(9-1)}krat 6+frac{(10-9)(10-1)}{( 3-9)(3-1)}krat 5+frac{(10-9)(10-3)}{(1-9)(1-3)}krat 12 y~=~ frac{(7)(9)}{(6)(8)}krat 6+frac{(1)(9)}{(-6)(2)}krat 5+frac{(1) (7)}{(-8)(-2)}krat 12$

y = (63/8) + (-15/4) + (21/4)

y = (63-30 + 42)/8

y = 75/8 = 9,375

Vrednost y pri x = 10 je 9,375

Primer 5: Poiščite vrednost y pri x = 7 za dani niz točk (1, 10), (2, 4), (3, 4), (5, 7)

rešitev:

podano,

(x₀, in₀) = (1, 10)
(x₁, in₁) = (2, 4)
(x₂, in₂) = (3, 4)
(x₃, in₃) = (5, 7)
Lagrangeova interpolacijska formula tretjega reda je,

$y~=~frac{(x-x_1)(x-x_2)(x-x_3)}{(x_0-x_1)(x_0-x_2)(x_0-x_3)}krat y_0+frac{(x-x_0 )(x-x_2)(x-x_3)}{(x_1-x_0)(x_1-x_2)(x_1-x_3)} imes y_1+frac{(x-x_0)(x-x_1)(x-x_3) }{(x_2-x_0)(x_2-x_1)(x_2-x_3)}krat y_2+frac{(x-x_0)(x-x_1)(x-x_2)}{(x_3-x_0)(x_3-x_1 )(x_3-x_2)}krat y_3$

Pri x = 7

$y~=~frac{(7-2)(7-3)(7-5)}{(1-2)(1-3)(1-5)}krat 10+frac{(7- 1)(7-3)(7-5)}{(2-1)(2-3)(2-5)}krat 4+frac{(7-1)(7-2)(7- 5)}{(3-1)(3-2)(3-5)}krat 4+frac{(7-1)(7-2)(7-3)}{(5-1)( 5-2)(5-3)}krat 7 y~=~frac{(5)(4)(2)}{(-1)(-2)(-4)}krat 10+ frac{(6)(4)(2)}{(1)(-1)(-3)}krat 4+frac{(6)(5)(2)}{(2)(1) (-2)}krat 4+frac{(6)(5)(4)}{(4)(3)(2)}krat 7$

y = -50 + 64 – 60 + 35

y = 99 – 110 = -enajst

Vrednost y pri x = 7 je -11

Primer 6: Poiščite vrednost y pri x = 10 za dani niz točk (5, 12), (6, 13), (7, 14), (8, 15)

rešitev:

podano,

(x₀, in₀) = (5, 12)
(x₁, in₁) = (6, 13)
(x₂, in₂) = (7, 14)
(x₃, in₃) = (8, 15)
Lagrangeova interpolacijska formula tretjega reda je,

$y~=~frac{(x-x_1)(x-x_2)(x-x_3)}{(x_0-x_1)(x_0-x_2)(x_0-x_3)}krat y_0+frac{(x-x_0 )(x-x_2)(x-x_3)}{(x_1-x_0)(x_1-x_2)(x_1-x_3)} imes y_1+frac{(x-x_0)(x-x_1)(x-x_3) }{(x_2-x_0)(x_2-x_1)(x_2-x_3)}krat y_2+frac{(x-x_0)(x-x_1)(x-x_2)}{(x_3-x_0)(x_3-x_1 )(x_3-x_2)}krat y_3$

Pri x = 10,

$y~=~frac{(10-6)(10-7)(10-8)}{(5-6)(5-7)(5-8)}krat 12+frac{(10- 5)(10-7)(10-8)}{(6-5)(6-7)(6-8)}krat 13+frac{(10-5)(10-6)(10- 8)}{(7-5)(7-6)(7-8)}krat 14+frac{(10-5)(10-6)(10-7)}{(8-5)( 8-6)(8-7)}krat 15 y~=~frac{(4)(3)(2)}{(-1)(-2)(-3)}krat 12+ frac{(5)(3)(2)}{(1)(-1)(-2)}krat 13+frac{(5)(4)(2)}{(2)(1) (-1)}krat 14+frac{(5)(4)(3)}{(3)(2)(1)}krat 15$

y = -48 + 195 – 280 + 150

y = 17

Vrednost y pri x = 10 je 17

Primer 7: Poiščite vrednost y pri x = 0 za dano množico točk (-2, 5), (1, 7)

rešitev:

podano,

(x₀, in₀) = (-2, 5)
(x₁, in₁) = (1, 7)
Lagrangeova interpolacijska formula prvega reda je,

$y~=~frac{(x-x_1)}{(x_0-x_1)}krat y_0+frac{(x-x_0)}{(x_1-x_0)}krat y_1$

Pri x = 0,

$y~=~frac{(0-1)}{(-2-1)}krat 5+frac{(0+2)}{(1+2)}krat 7$

y = (5/3) + (14/3)

y = 19/3 = 6,33

Vrednost y pri x = 0 je 6,33

Pogosta vprašanja o Lagrangeovi interpolacijski formuli

1. Kaj je Lagrangeova interpolacijska formula?

Lagrangeova interpolacijska formula je formula, ki se uporablja za iskanje vrednosti odvisne spremenljivke funkcije za katero koli neodvisno spremenljivko, čeprav sama funkcija ni podana.

2. Kakšne so aplikacije Lagrangeove interpolacijske formule?

Lagrangesova formula ima različne aplikacije v sodobni matematiki in podatkovnih znanostih,

Uporablja se za usposabljanje modela AI.
Uporablja se pri obdelavi slik.
Uporablja se pri graficiranju 3-D in višjih krivulj itd.

3. Kaj je Lagrangeova interpolacijska formula prvega reda?

Lagrangesova interpolacijska formula prvega reda je,

f(x) = (x – x ₁ )/(x ₀ – x ₁ )×f ₀ + (x – x ₀ )/(x ₁ – x ₀ )×f ₁

4. Kaj je Lagrangeova interpolacijska formula drugega reda?

Lagrangesova interpolacijska formula drugega reda je,

f(x) = [(x – x ₁ )(x – x ₂ )/(x ₀ – x ₁ )(x ₀ – x ₂ )]×f ₀ + [(x – x ₀ )(x – x ₂ )/(x ₁ – x ₀ )(x ₁ – x ₂ )]×f ₁ + [(x – x ₀ )(x – x ₁ )/(x ₂ – x ₀ )(x ₂ – x ₂ )]×f ₀