Ali je vsak pravokotnik romb? Pravokotnik je dvodimenzionalna geometrijska figura, ki jo upodabljajo štiri stranice in štirje vogali. Pravokotnik vsebuje stranice, tako da sta dolžini nasprotnih strani enaki in da sta stranici vzporedni. Stranice, ki si delijo vogal s sosednjimi stranicami s kotom 90° med njima. Zato so v pravokotniku štirje pravi koti.

Kazalo
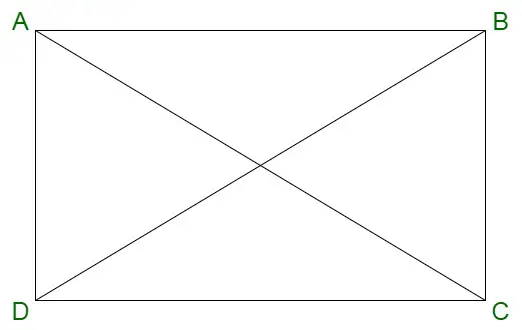
Pravokotnik
Lastnosti pravokotnika so podane spodaj:
- Ima štiri robove in štiri vogale, znane kot oglišča.
- Diagonali pravokotnika se med seboj razpolavljata.
- Ploščina pravokotnika je enakovredna produktu njegove dolžine in širine.
- Vsako oglišče ima kot enak 90O
- Nasprotni stranici pravokotnika sta med seboj enaki in vzporedni.
- Obod je enakovreden dvakratni vsoti njegove dolžine in širine.
- Vsota vseh notranjih kotov je enaka 360 stopinj
Obseg pravokotnika
Celoten premik, ki ga zajame prehod skozi mejo pravokotnika, lahko imenujemo obod. Ker sta tako dolžina kot širina označeni z enoto dolžine, se tudi obseg meri v enoti dolžine.
Obod lahko označimo z,
Obseg, P = 2 (dolžina + širina)
Območje pravokotnika
Območje, ki ga pokriva dvodimenzionalni geometrijski lik v ravnini, se imenuje območje lika. Tako je površina pravokotnika površina, vključena v njegove meje. Meri se v kvadratnih enotah. Ploščina je enakovredna produktu dolžine in širine pravokotnika.
Območje lahko označimo z,
Površina, A = dolžina × širina kvadratne enote
Formula diagonale pravokotnika
Diagonale katere koli geometrijske figure povezujejo nadomestna oglišča. Dolžino diagonal pravokotnika lahko izračunamo z naslednjo formulo, označeno z d,
d = sqrt{( l^2 + w^2)} kje,
l = dolžina pravokotnika
w = širina pravokotnika
Preberite podrobno: Lastnosti pravokotnika: definicija, formule, primeri
Romb
Romb je znan tudi kot štiristranski štirikotnik. Velja za poseben primer paralelograma. Romb vsebuje vzporedne nasprotne stranice in enake nasprotne kote. Romb poznamo tudi pod imenom diamant ali romb diamant. Romb vsebuje vse stranice romba kot enako dolge. Tudi diagonali romba se razpolovita pod pravim kotom.
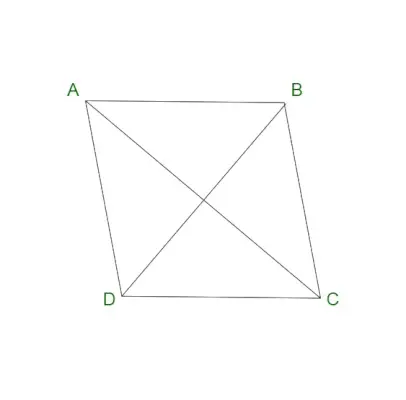
Lastnosti romba
Romb ima naslednje lastnosti:
- Romb vsebuje vse enake stranice.
- Diagonale romba se medsebojno razpolavljajo pod pravim kotom.
- Nasprotni stranici romba sta po naravi vzporedni.
- Vsota dveh sosednjih kotov romba je enaka 180O.
- Znotraj romba ni vpisanega kroga.
- Okrog romba ni opisanega kroga.
- Diagonale romba vodijo do oblikovanja štirih pravokotnih trikotnikov.
- Ti trikotniki so med seboj skladni.
- Nasprotna kota romba sta enaka.
- Ko povežete sredino stranic romba, nastane pravokotnik.
- Ko se središčni točki polovice diagonale povežeta, nastane še en romb.
Obseg romba
Obseg romba je opredeljen kot skupna dolžina njegovih meja, ki tvorijo lik. Označimo ga lahko tudi kot skupni seštevek dolžin štirih stranic romba. Obseg romba je določen z:
Obseg, P = 4a enot
kjer so diagonale romba označene z d1& d2in 'a' je stran.
Območje romba
Območje romba je opredeljeno kot območje, zaprto v dvodimenzionalni ravnini. Ploščina romba je enakovredna zmnožku diagonal romba, deljenih z 2. Ploščino romba je mogoče definirati z naslednjo formulo:
Območje, A =
frac{(d_1 imes d_2)}{2} kvadratnih enotkjer d1in d2so diagonali romba.
Zlahka opazimo, da je vsak romb paralelogram, vendar obratno ne drži. Kvadrat lahko obravnavamo kot poseben primer romba, saj ima štiri enako dolge stranice. Kvadrat ima vse prave kote. Ni pa nujno, da so vsi koti romba pravi koti . Končno lahko romb, ki vsebuje prave kote, obravnavamo kot kvadrat. Zato lahko rečemo, da
- Vsi rombovi so paralelogrami.
- Vsi paralelogrami niso rombovi.
- Vsi rombi niso kvadrati.
- Vsi kvadrati so rombi.
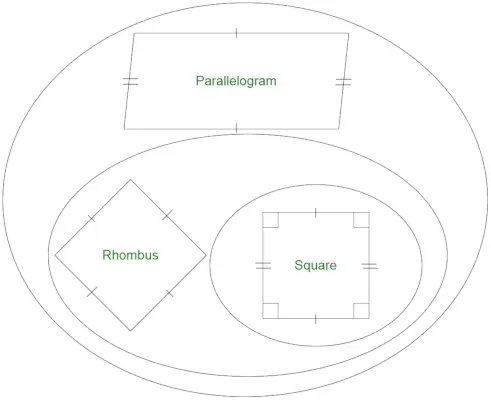
Ali je vsak pravokotnik romb?
Pravokotnik je geometrijski lik, ki nima vseh enakih stranic. Kvadrat je poseben primer pravokotnika z vsemi enakimi stranicami. Saj vemo, da ima romb vse stranice enake. Množice pravokotnikov in rombov se sekajo le pri kvadratih. Zato pravokotnik ni romb.
arraylist in linkedlist

Zakaj je romb pravokotnik?
Romb je poseben primer pravokotnika. Ker vemo, da se diagonali romba sekata pod enakimi koti, medtem ko sta diagonali pravokotnika enako dolgi. Ko povežemo razpolovišča stranic romba, nastane pravokotnik.
Preberi več: Zakaj romb ni kvadrat?
Primeri vprašanj – Ali je vsak pravokotnik romb
Vprašanje 1. Izračunajte ploščino pravokotnega okvirja, ki ima 6 palcev dolžine in širine 3 cm.
rešitev:
Ker vemo,
Ploščina pravokotnika = (dolžina × širina) kvadratnih enot.
Z zamenjavo vrednosti dobimo,
površina pravokotnega okvirja = 6 × 3 = 18 kvadratnih palcev
Vprašanje 2. Poiščite dolžino diagonale pravokotnika, ki ima dolžino 12 cm in širino 8 cm.
rešitev:
Vemo,
Diagonalna dolžina,
D =
sqrt{ L^2+W^2} ⇒ D =
sqrt{12^2+8^2} ⇒ D =
sqrt{144 + 64} ⇒ D = √208
⇒ D = 4√3
Vprašanje 3. Poiščite ploščino romba z dvema diagonalama d 1 in d 2 6 cm oziroma 12 cm.
rešitev:
Imamo,
Diagonala d1= 6 cm
Diagonala d2= 12 cm
Območje romba je podano z
A =
frac{(d_1 imes d_2)}{2} kvadratnih enotA =
frac{( 6 imes 12)}{2} A =
frac{72}{2} A = 36 cm2
Torej je ploščina romba = 36 cm2.
Vprašanje 4. Razlika med rombom in pravokotnikom?
rešitev:
| Lastnina | Romb | Pravokotnik |
| Strani | Enake stranice. | Nasprotni stranici sta enaki. |
| Diagonale | Diagonali se razpolovita pod kotom 90°. Diagonale sestavljajo v sredini prave kote. | Diagonali se razpolovita pod različnimi koti. En kot je top kot, drugi pa oster kot. Diagonale tvorijo v sredini različne kote - top in oster kot. |
| Koti | Nasprotna kota sta enaka. Seštevek sosednjih kotov znaša 180°. | Nasprotni in sosednji koti so enaki. Kot, ki ga tvorita sosednji stranici pravokotnika, je 90°. |
